Recently, the study of systems exhibiting parity-time (PT) symmetry has drawn a great deal of attention. The underlying idea is to extend canonical quantum mechanics by introducing a class of non-Hermitian Hamiltonians which exhibit entirely real eigenvalue spectra below a certain phase-transition point [1], although the potentials in these Hamiltonians are complex-valued. A necessary condition for the Hamiltonian to be PT-symmetric is that its potential V(x), being complex, is subject to the spatial-symmetry constraint V(x) = V^*(-x). The complex PT-symmetric potentials can be realized in the most straightforward way in optics, by combining the spatial modulation of the refractive index with properly placed gain and loss [2]. This possibility has excited extensive theoretical [3,4] and experimental [5] research. Pioneering theoretical works [2,3,4] stimulated recent experimental studies that eventually resulted in the observation of the PT symmetry breaking in both active [5] and passive [6] optically coupled systems. This will probably enable manufacturing of integrated PT photonic devices with extraordinary capabilities, such as double-refraction or energy flow tailoring. A new direction in nonlinear optical research, concerning PT optical lattices [7] and the related PT-based solitons, can be envisaged. The existence and propagation dynamics of the one-dimensional (1D) optical solitons in a PT-symmetric linear periodic potential have been examined in detail in Ref. [8]. Hence, further exploration of general properties of solitons in multidimensional PT-symmetric potentials is warranted.

An intriguing feature of PT-symmetric potentials is the spontaneous breakdown of PT symmetry above a threshold level of the strength of the imaginary part of the potential. Above that level the eigenfunctions of the Hamiltonian cease to be the eigenfunctions of the PT operator, even though the PT symmetry remains in force. The complex Coulomb potential, which will be used as the PT potential in this paper, was among the early potentials studied in the PT-symmetric setting [9]. It turned out, however, that in 1D it cannot be treated on the real x-axis, but on some trajectories in the complex x plane [10,11]. In the multidimensional case it is treatable in the quantum mechanical sense, but as a part of a more complicated PT-symmetric potential involving parabolic and quartic potentials [11]. We treat it as a nonlinear optical problem, which may not make much sense quantum mechanically, but represents a viable system optically.

Optical spatial solitons, which are self-trapped optical beams that exist by virtue of the balance between diffraction and nonlinearity, have lately been extensively studied in nonlocal nonlinear media [12,13]. It has been found that the nonlocality can prevent the collapse of self-focusing beams in media with cubic nonlinearity [14], suppress azimuthal instabilities of vortex solitons [15], and stabilize Laguerre soliton clusters, azimuthons, and multipole solitons [12].

The evolution of optical beams in nonlocal nonlinear media is governed by the nonlocal nonlinear Schrodinger (NNS) equation [12,16]. Of particular importance is the case, referred to as the strongly nonlocal case, in which the characteristic length of nonlocality is much larger than the beam width. In 1997, Snyder and Mitchell [16] simplified the NNS equation in the case of strong nonlocality to a linear model, called the Snyder-Mitchell model [13]. Subsequently, Assanto et al demonstrated theoretically [17] and experimentally [18] that nematic liquid crystals are some of the strongly nonlocal nonlinear (NN) media. The Snyder-Mitchell model can support solitons with new properties, the so-called “accessible solitons” [16], which are described by the solutions of a linear differential equation, tantamount to the high-dimensional quantum harmonic oscillator [12,13]. Owing to this feature, strong nonlocality exerts a stabilizing influence on the dynamics of solutions, as the solutions of linear systems cannot be unstable or chaotic.

Light bullets (LBs), or optical spatiotemporal solitons [19], in which both the diffraction and group-velocity dispersion are balanced by the nonlinearity, are challenging subjects in multidimensional nonlinear optics [20]. In addition to their fundamental significance as particle-like waves, light bullets can find applications in long and short-distance communications, all-optical switching, and digital computing, among others [21]. In this paper we demonstrate that a class of new 3D light bullets originating in a PT-symmetric potential can be supported by the strongly nonlocal nonlinear media. We display rather unusual properties of these 3D light bullets. However, the main aim of the present work is to perform a detailed study of the 3D NNS equation in the strongly NN media in the presence of a PT-symmetric potential and in a region where optical solitons can exist. Thus, we concentrate on obtaining the localized solutions of the 3D strongly NNS equation, without regarding them a priori as stationary eigenfunctions of the corresponding Hamiltonian operator, with the corresponding real or complex eigenvalues.

The rest of the article is organized as follows. In Section II, the 3D Snyder-Mitchell model with a PT-symmetric potential is introduced, and the localized soliton solutions are constructed. The properties of 3D localized accessible solitons with the PT-symmetric potential are explored. We also illustrate and discuss some examples of the exact solutions obtained in Section III. The article is concluded in Section IV.

We begin the analysis from the scaled (3+1)D spatiotemporal nonlinear Schrodinger equation [13,22,23]

which governs the propagation of a slowly varying field envelope u along the propagation coordinate z in a nonlinear nonlocal optical medium. Here ∇² is the full 3D spatiotemporal Laplacian,

is the radial coordinate, z is the retarded time in the reference frame moving with the pulse, and

represents the nonlocal nonlinearity induced by the optical beam intensity I=|u|². W denotes the external potential. We assume N to be of the form

where

is the normalized symmetric real response function of the medium whose characteristic length determines the degree of nonlocality. The setting chosen in this paper is reminiscent of the X wave generation geometry [24]; the wave equations are similar and there exist natural linear and nonlinear regimes of wave packet dynamics. The major difference is that we consider a nonlocal medium with anomalous dispersion.

In the case of strong nonlocality, Eq. (1) can be simplified to the 3D Snyder-Mitchell model in spherical coordinates [13,22,25]:

where s is a parameter proportional to the beam power. To analyze PT-symmetry relevant for Eq. (2), we choose the complex Coulomb potential

where μ (≠0) is a real constant. Obviously, when μ = 0, Eq. (2) is simplified to the general 2D NNS equation in strongly NN media [25]. The second term in Eq. (2) represents diffraction, the third term originates from the optical nonlinearity, and the fourth term is the external potential function. It is noted that Eq. (2) is rather generic; one may assign different physical interpretations to essentially the same type of equation by choosing different physical systems and variables. For example, in a typical quantum mechanical setting one may understand Eq. (2) as the scaled Schrodinger equation for the wave function of a particle moving in the potential

An often analyzed similar PT version involves both quadratic and quartic anharmonic oscillator terms

[26]. Hence, it is the parameter μ that decides whether Eq. (2) is PT-symmetric or not. It is easy to see that V^*(-r) = V(r). Thus, Eq. (2) is a system with the PT-symmetric potential.

We treat equation (2) in spherical coordinates, by the method of separation of variables. Defining the complex optical field as u(z,r,θ,？) = F(z,r) Y(θ,？), with separated angular variables, the separation yields the following two equations:

where l is a non-negative integer. Equation (3A) has the spherical harmonics as the solution,

where

are the associated Legendre polynomials with

and ？ is the azimuthal angle. The parameter 0≤q≤1 determines the modulation depth of the beam intensity. The parameter m is a real nonnegative integer, called the topological charge.

Now, we consider the solution of Eq. (3B). Following Refs. [12,25], we define F(z,r) = A(z,r)e^iB(z,r), where A(z,r) and B(z,r) are the real functions of z and r. With this variable change and after a little algebra, we transform Eq. (3B) into two coupled equations for A and B:

These equations can be treated by the self-similar method [25]. To treat Eqs. (5), the amplitude A(z,r) and the phase B(z,r) of the beam are further defined as [25]:

where Ω(z,r) is the self-similarity variable and w(z) is the pulse width. As a consequence of these definitions, Eq. (5B) yields:

Note that the parameter b remains invariant on propagation. Furthermore, it should be noted that Eqs. (7) and (8) are universally applicable to all types of self-similar pulses. Here and in what follows, the symbols containing subscript “0” are used to represent the initial values of the corresponding parameters, at distance z = 0.

By means of Eqs. (6), (7) and (8), a nonlinear differential equation for F is derived from Eq. (5A),

where c_z is the derivative of c with respect to z. In order to solve Eq. (9), we introduce another variable transformation

from Eq. (9) one obtains:

To simplify Eq. (10), yet another variable transformation is introduced, Ω² = R; thus, we find:

In the end, to obtain tractable solutions, we restrict their generality by choosing special forms of some parameters:

where n is a nonnegative integer and w₀ (=constant) is the initial beam width of the pulse. Using Eq. (12B) we find that Eq. (11) becomes:

The solution of Eq. (13) can be written in terms of the confluent hypergeometric functions. Thus, when w = w₀, an exact single accessible light bullet solution to Eq. (2) with a PT-symmetric potential can be written as:

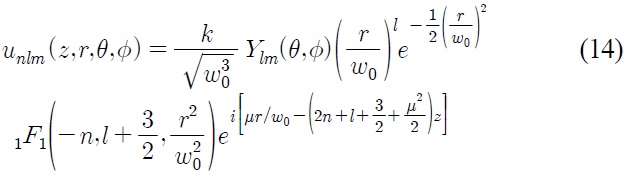
where Y_lm(θ,？) are the spherical harmonics and ₁F₁ is the confluent hypergeometric function of the first kind. It is straightforward to see that |u(z,r,θ,？)| vanishes at r → ∞, i.e., Eq. (14) represents a localized solitary solution. Arbitrariness in the choice of the soliton parameters n, m and l included in the above solution (3) implies that the beam field u(z,r,θ,？) may possess a rich structure. For μ = 0 the solution (14) goes to the solution (21) in Ref. [25], apart from a constant factor. It should be noted that the solution (14) differs from the solution in the absence of the PT potential, i.e. when μ=0, by a complex factor exp [i(μr/w₀ -μ²z/2)]. Thus, the influence of the complex Coulomb potential is to modulate the accessible solitons that exist in the absence of it. The intensity distributions |u_nlm|² remain the same in both cases.

To better understand the 3D soliton dynamics, we introduce some special types of localized solutions for the

optical field expressed by Eq. (14) via suitable selections of the nonnegative integer parameters (n,m,l). We focus attention on the distributions of the optical intensity I = |u|². In the following examples, we further fix the beam width w₀ = 1.

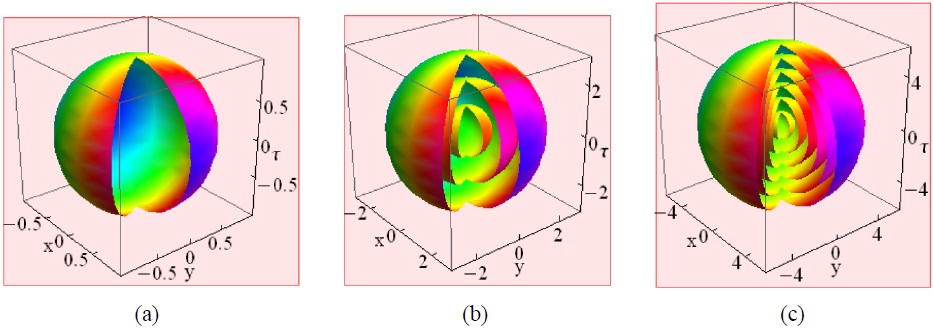
First, we address the simplest case m = 0. Then the LB intensity does not depend on the modulation depth q. Because the parameters n and l are arbitrary, various light bullet structures can be obtained. If the parameters n and I are chosen as zero, from Eq. (14) we find that ₁F₁(0,3/2,r²) = 1; the beam is then called the fundamental light bullet and forms a single-layer sphere, see Fig. 1(a). Keeping l = 0 and increasing the parameter n, multilayered structures are obtained; a typical example is presented in Fig. 1(b) for n = 2. Similarly, we can construct a higher-order fundamental LB for larger n, i.e., for n = 4 the intensity distribution is exhibited in Fig. 1(c). In general, there exist n+1 layered spheres for such a soliton.

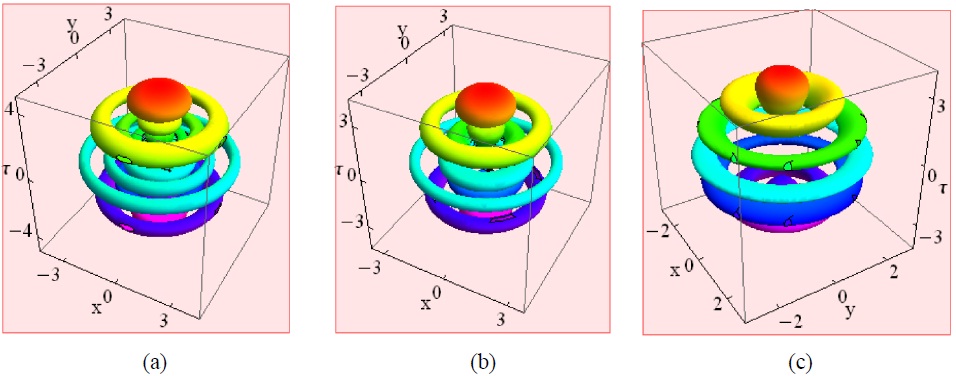
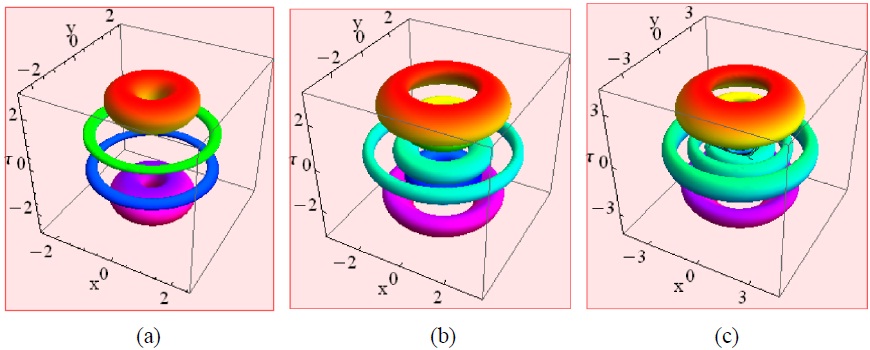
For n≠0 and l≠0, the higher-order LBs can be excited. Figure 2(a) displays the results for n = 2, l = 4, which features three coaxial rings in the mid-plane; there are five layers stacked along the τ-axis. Figure 2(b) displays similar structures for n = 1, l = 4, with two rings in the mid-plane, and two disks above and below the central rings. Finally, Fig. 2(c), corresponding to n = 0, l = 6, shows a single middle ring and, once again, ring and disk-shaped objects along the τ-axis.

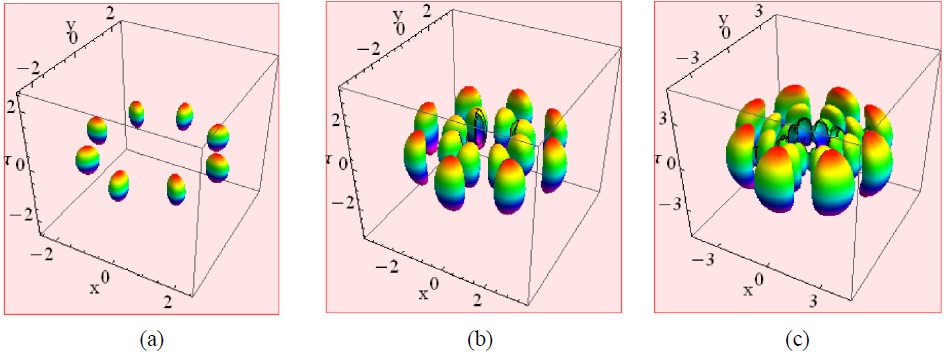
For q = 1 in Eq. (14), we obtain the vortex ring beam for a nonnegative integer l and a positive integer m. As an interesting case we pick the parameters m = l (≠0). An example of such a vortex ring LB is shown in Fig. 3. The soliton parameters are: (a) m = l = 4, n = 0; (b) m = l = 3, n = 1; (c) m = l = 2, n = 2. The number of rings in the horizontal direction is determined by n. Changing the modulation depth from q = 1 to 0 < q < 1, we find that the LBs modulate azimuthally, see Fig. 4. It is noted that the outer modulation is more distinct than the inner one. Actually, the formation of a vortex ring beam is the result of the periodic azimuthal modulation functions cos(m？) and sin(m？).

For m > 0 (m ≠ l) an integer, and in the limit q = 1,

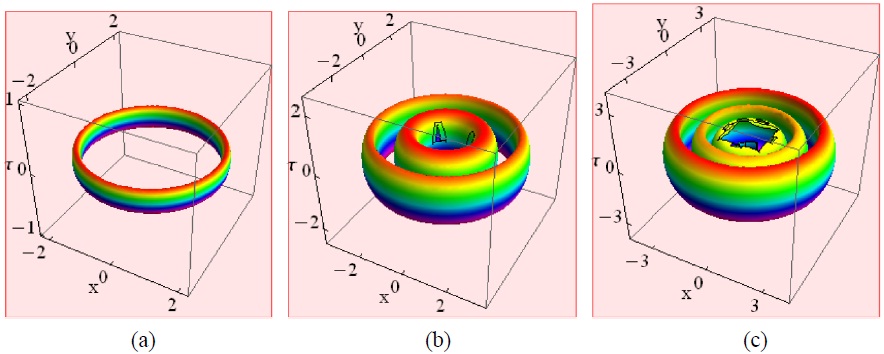
the multilayered vortex ring LBs along the vertical τ-axis are found. In Fig. 5 we depict some properties of the vortex ring LBs. It is seen that for the same m, the larger the parameter n, the larger the soliton radius in the horizontal plane. The optical intensity is zero at the τ-axis, which is the location of the topological defect.

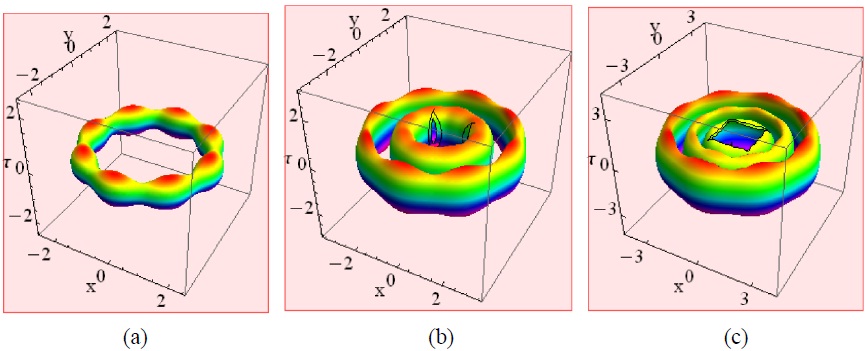
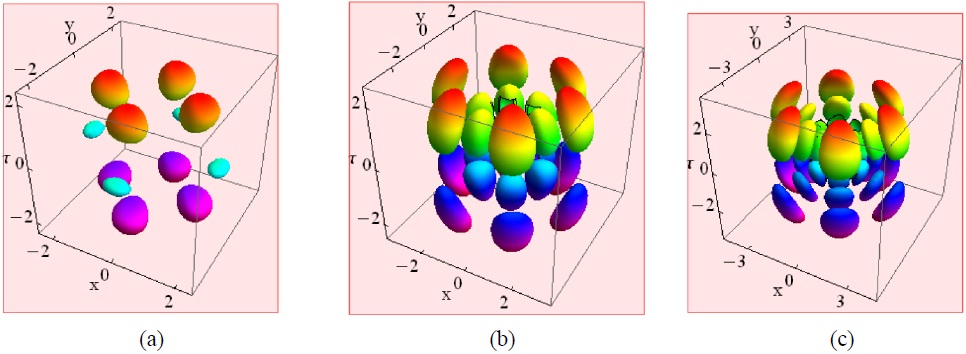
For q = 0 and l = m in Eq. (14), we obtain single-layer and multi-layer necklace beams for a positive integer m. A typical example of such a necklace is shown in Fig. 6 for l = m = 4, along with the axisymmetric distribution.

Self-trapped localized structures with a large number of azimuthal petals and multi-layered necklaces may exhibit a strong effective stabilization in strongly NN media [12,13]. Figure 7 displays the intensity distribution of multi-layer

necklace solitons in the vertical direction, which exhibit similar patterns. These examples are obtained for positive integers (n,l,m) in Eq. (14). The parameters are: (a) (0,4,2); (b) (1,4,3); (c) (2,4,3). In these solutions, the necklace structure is still formed, due to the periodic azimuthal modulation. Note that these solitons form multi-layers, with the outer ones more strongly modulated than the inner counterparts.

Interesting structures are seen in Figs. 6 and 7. We find that the larger the parameter m, the larger the necklace radius. It is seen that the soliton distributions change regularly with the azimuthal angle. The number of beads in each layer is determined by m, and the number of layers is determined by n. These solitons contain 2m(n+1) necklaces and form n+1 necklace layers in the horizontal direction. The number of necklace layers in the vertical direction is determined by l.

We have introduced a class of self-trapped LB solutions of the NNS equation in the strongly NN media with a PT-symmetric potential in the form of a complex Coulomb potential. We were not much concerned with the details of the eigenvalue spectrum, but with the solution of the NNS equation with a specific PT-symmetric potential. Analytical accessible soliton solutions are obtained with the help of the self-similar method for solving such evolution partial differential equations. They are given in terms of the confluent hypergeometric function of the first kind and spherical harmonics. We find that in addition to the fundamental LBs, these solutions may come in the form of 3D single-layer and multi-layer disk-shaped, vortex ring and necklace LBs.