The image quality of a lens design can be good but the cost of the glass from which it is made can be quite high. Kidger [1] considered variation in cost between glasses used for this purpose. In the large size lenses, the cost of expensive glass could be prohibitive; but in small size lenses, the materials make up only a small percentage of the total cost of the lens, so expensive materials might well be acceptable in this case. Chromatic aberration occurs because of the different refractive indices of lenses for different wavelengths of light [2,3]. If two different types of glasses are combined into a thin two-element system, a paraxial chromatic aberration will develop [4]. Robb [5] developed a method using two different types of glass for the correction of axial color for at least three wavelengths. Certain combinations might be found for correction at four and five wavelengths. In 1983, Sharma and Gopal [6] used the double-graph technique to produce doublet designs. Then, in 2001, Rayces and Rosete-Aguilar [7,8] described a method to select pairs of glasses for both thin cemented achromatic doublets and thin aplanatic achromatic doublets with a reduced secondary spectrum. In another study, Banerjee and Hazra [9] used a genetic algorithm for the structural design of cemented doublets. The aim of this work is to minimize chromatic aberration by using a low-cost optimal double-prism method. An efficient approach for finding an optimum design is also proposed.
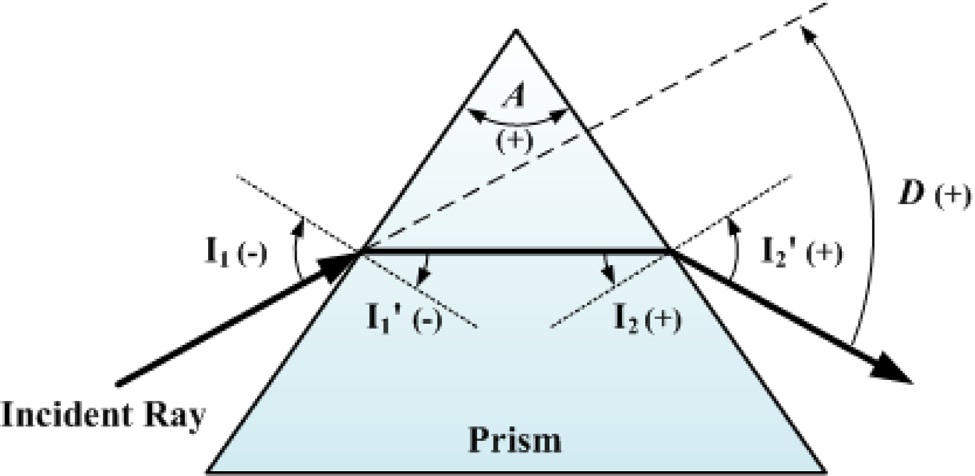
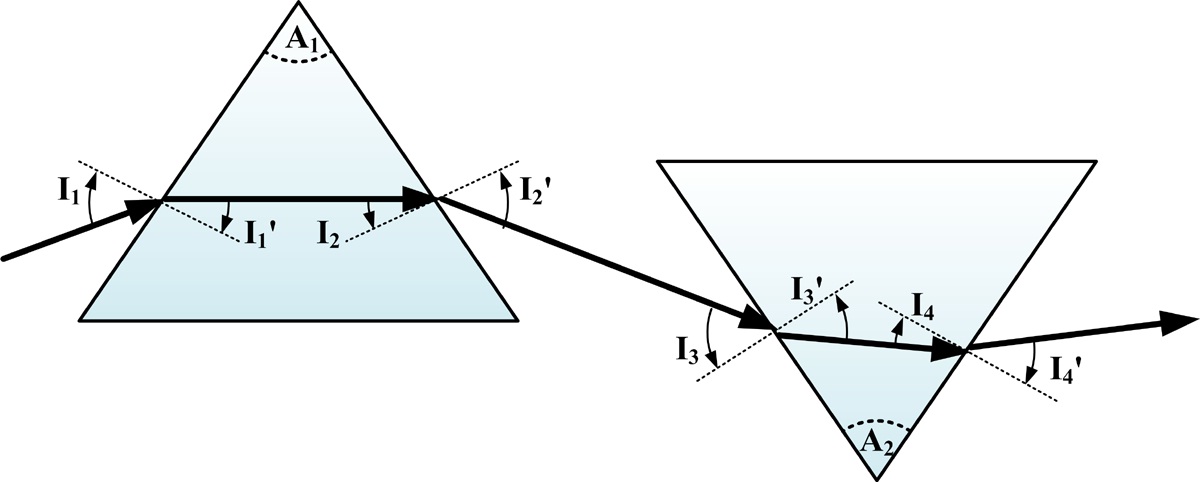
An illustration of ray tracing in and out of a prism is shown in Fig. 1. The angle of a ray in the normal direction from the prism surface is positive in the anticlockwise
direction, and negative in the clockwise direction. In this figure,
If we consider real ray tracing, the deviation angle [10] presented by
2.1. Single Prism Paraxial Chromatic Aberration
If all the angles of the design are small, the equations for the paraxial ray tracing can be obtained, and the paraxial deviation angle [11] given by
The paraxial primary color
where
where
2.2. Doublet Prisms Paraxial Chromatic Aberration
In the paraxial ray tracing of doublet prisms, the angle of deviation of d-line light is defined as 3°, so the primary color
where the paraxial deviation angles of the doublet prisms are
and
The apex angles of the doublet prisms are expressed as
and
Accordingly the paraxial primary color is zero, but there are still some paraxial secondary spectra. Thus the paraxial secondary spectrum can be defined as
where the paraxial primary chromatic aberrations of the doublet prisms are
We choose the Schott glass [12] for the design because of the large number of types of glasses that are available. The Abbe numbers of the different glasses have been ranked. There are 119 different optical glasses all with different prices. The price of N-BK7 is the lowest. The relative price (RP) is found by comparison and the results are indexed. To avoid using the most expensive types of glass in the design, the twenty-nine types with a relative price RP ≥ 17 as well as those with no marked prices are eliminated. The costs of glasses such as N-KZFS11, N-PK51, and N-LASF31A, are much higher than the others. Those with no marked prices are molding glasses or new types of glasses. The internal transmittance is the transmittance of light excluding reflection loss. The N-SF6HT and N-SF57HT glasses offer improved transmittance in the visible spectral range especially in the blue-violet area. Moreover, since the
In Eqs. (2) and (3), it can be seen that the there is a difference in the deviation angles between the real ray and the paraxial ray. The deviation angle of the paraxial ray is unconcerned with the incident angle
where
Before optimization, the
We then get the equation
where
3.1. Minimizing the Paraxial Chromatic Aberration
The doublet prisms have two apex angles. The angle of deviation of d line is 3°, and the primary color is eliminated. The steps are repeated to reduce the secondary spectra of the doublet prisms. Using Eq. (12), the correct doublet prisms combination can be found by choosing the smaller (
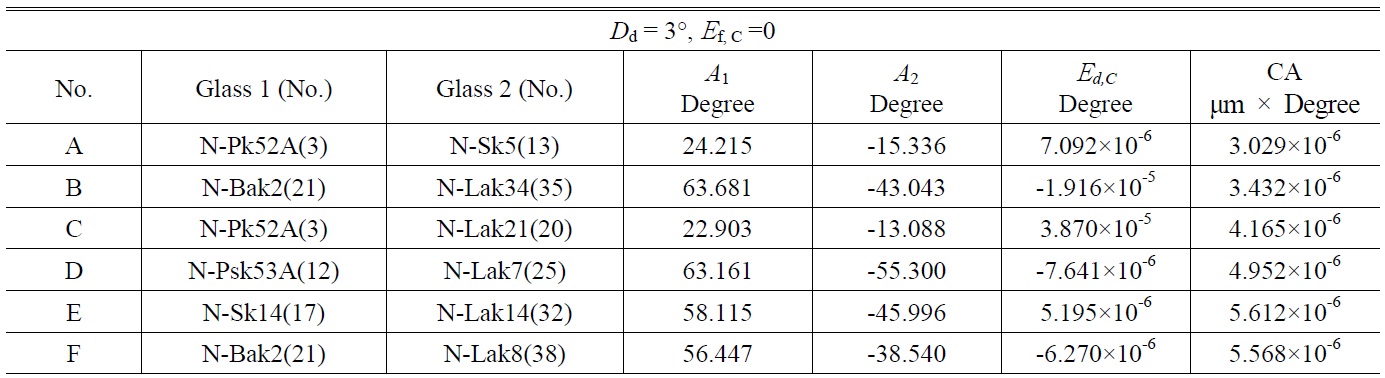
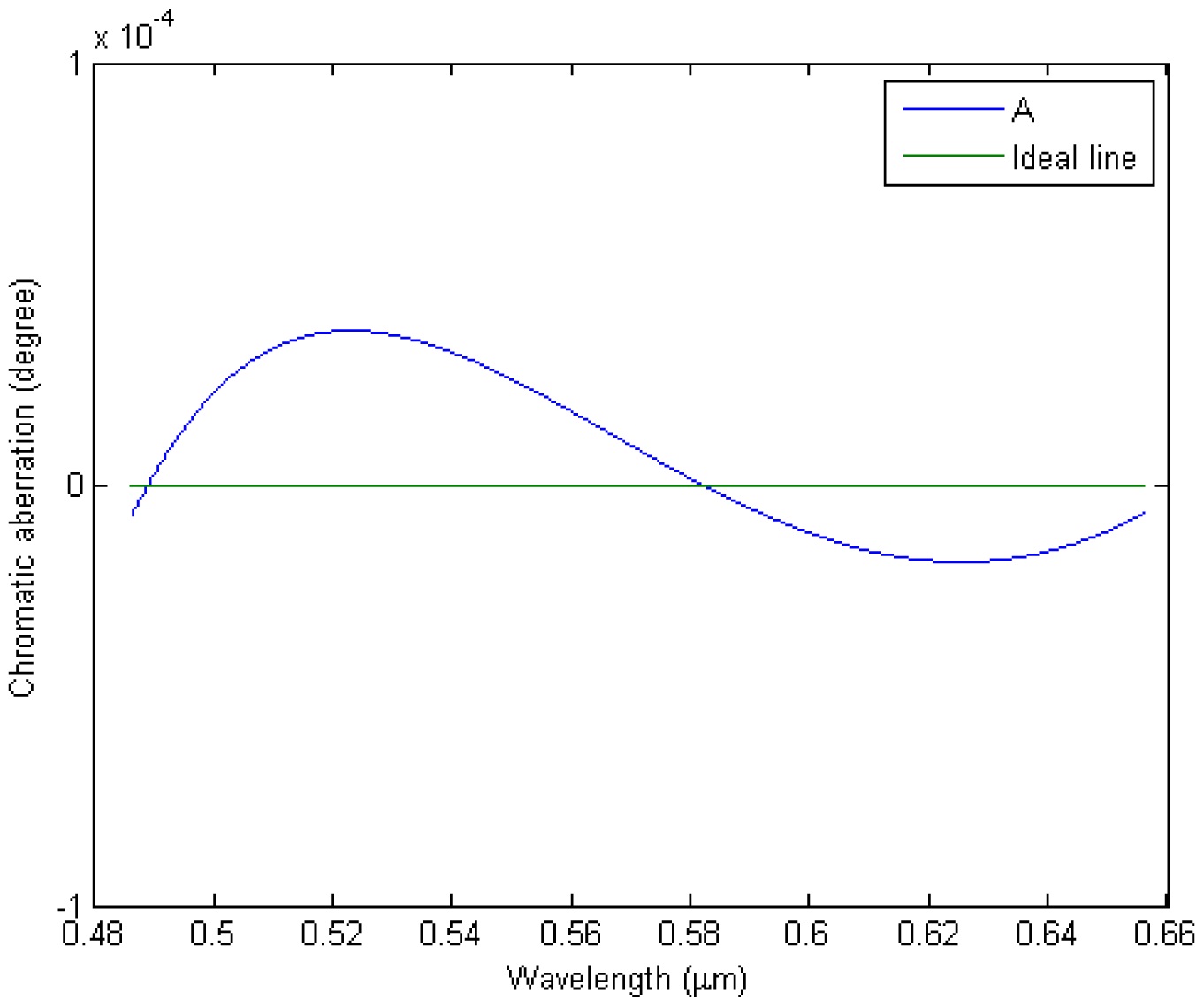
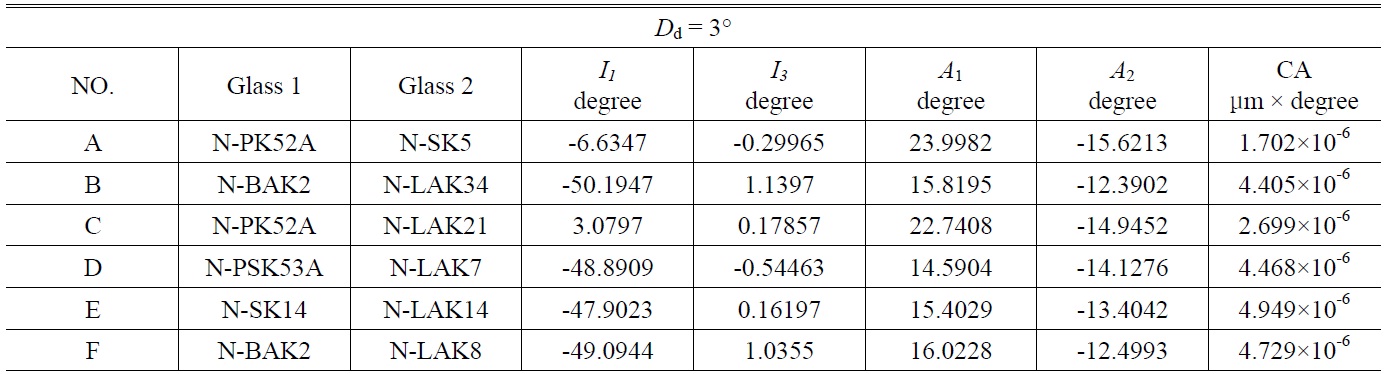
[TABLE 1.] Design data and area of paraxial chromatic aberration curves for doublet prisms A To F
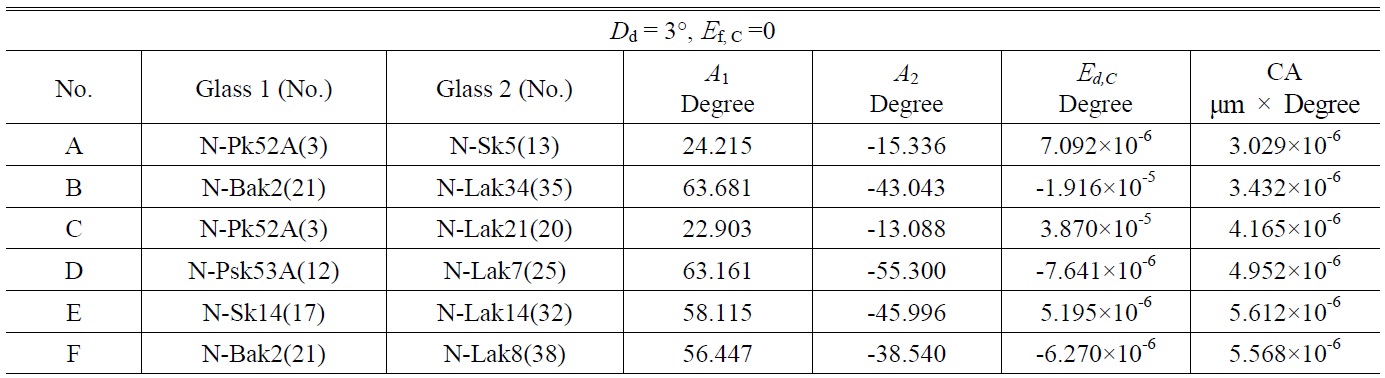
Design data and area of paraxial chromatic aberration curves for doublet prisms A To F
[TABLE 2.] Initial values for optimization of the doublet prism design (group A)

Initial values for optimization of the doublet prism design (group A)
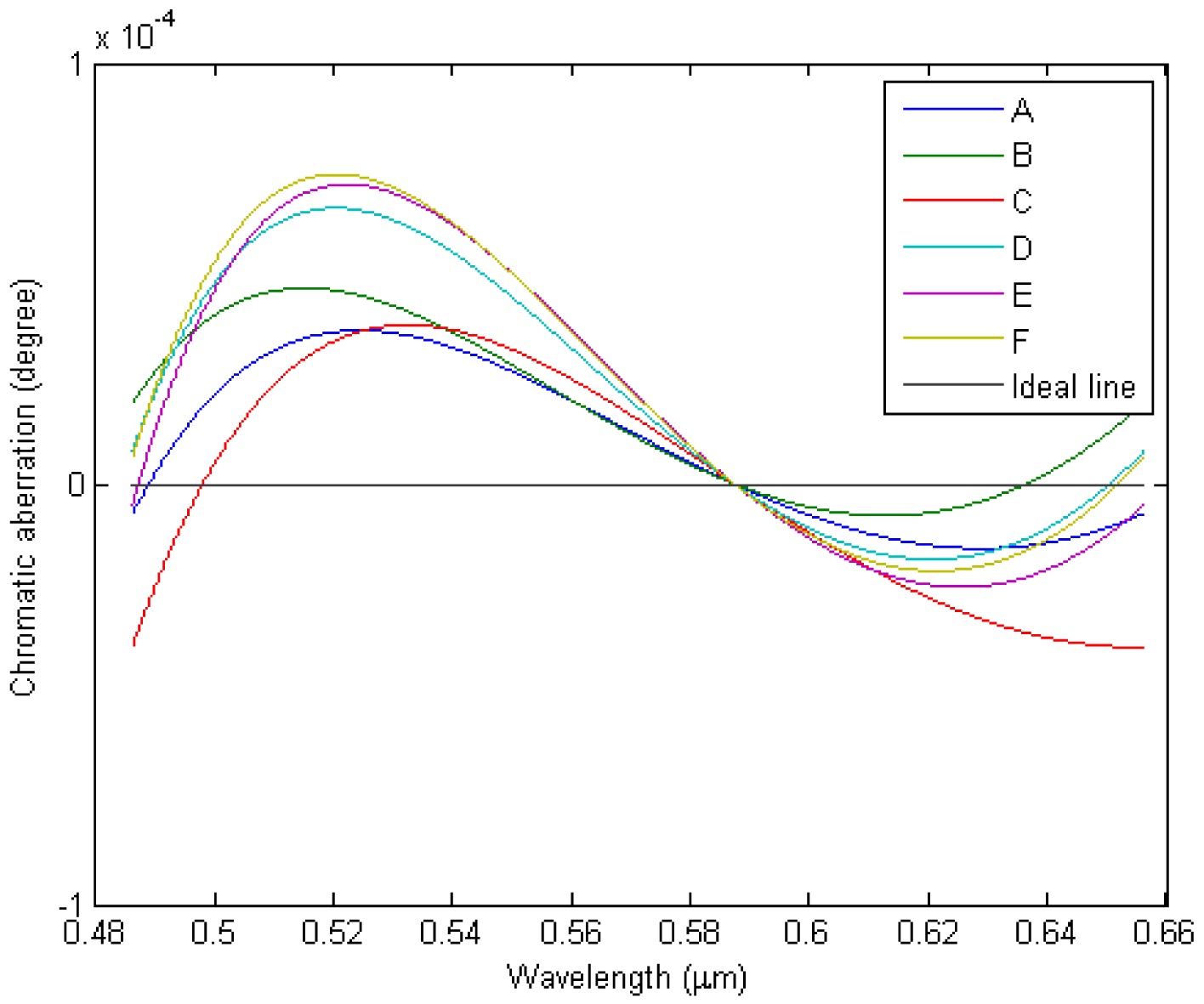
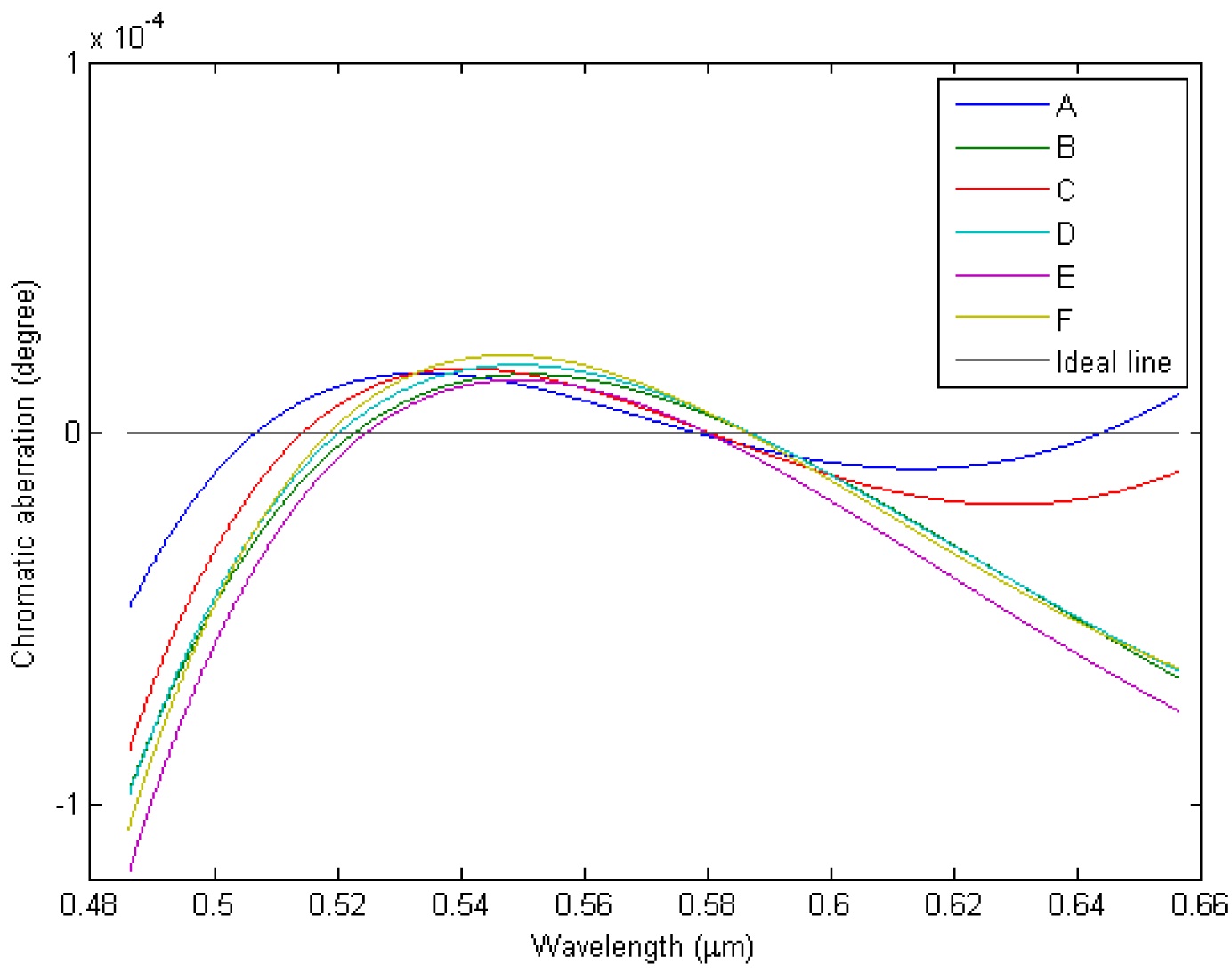
horizontal ideal line, which denotes the angle of deviation of d line is 3°, has been set to zero for the chromatic aberration. The other lines are described as the chromatic aberration of doublet prisms groups from A to F.
3.2. OPtimization Design For The Real Chromatic Aberration
We choose group A from Table 1 as an example as the initial value. The doublet prisms are made of N-PSK52A and N-SK5 glasses. We set
The merit function consists of three terms. The first term is the deviation angle
where the weighting factors are
will consider some sort of aberration balance, a sensible choice of weighting factors is essential if we are to achieve the best possible performance. In the optimization process, we think that two aberrations of
We use four variables as
Except for fixing the deviation angle of real ray
[TABLE 3.] Design results (group A) for target values: tDd=3, t?d,D=0, and t?F,C=0

Design results (group A) for target values: tDd=3, t?d,D=0, and t?F,C=0
[TABLE 4.] Design results (group A) for target values: tDd=3, tCA=0

Design results (group A) for target values: tDd=3, tCA=0
where the target values are
3.3. Total Internal Reflection
As mentioned before, figure 4 shows the ray tracing of the doublet prisms, where
where
We choose group B from Table 5 as an example. The two types of glass used in the doublet prisms are N-BAK2 and N-LAK34, their refractive indices are
the first prism must be
and the incident angle
3.4. Design of The Optimization Program
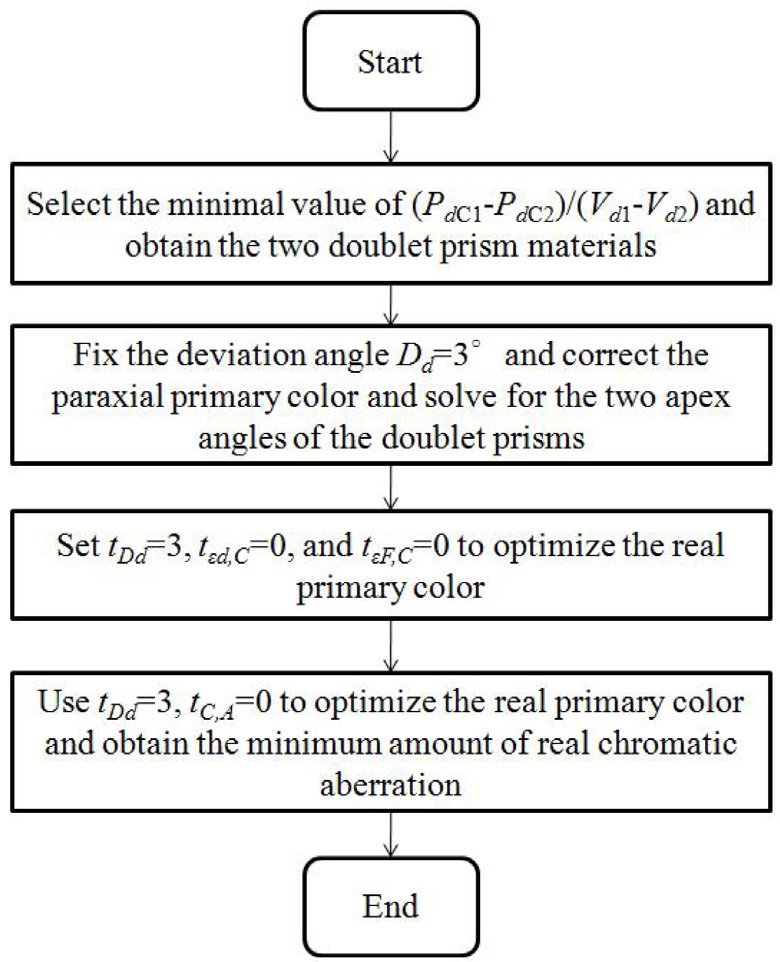
A flow-chart of the optimization program for the doublet prisms design is shown in Fig. 7. First, the program selects (
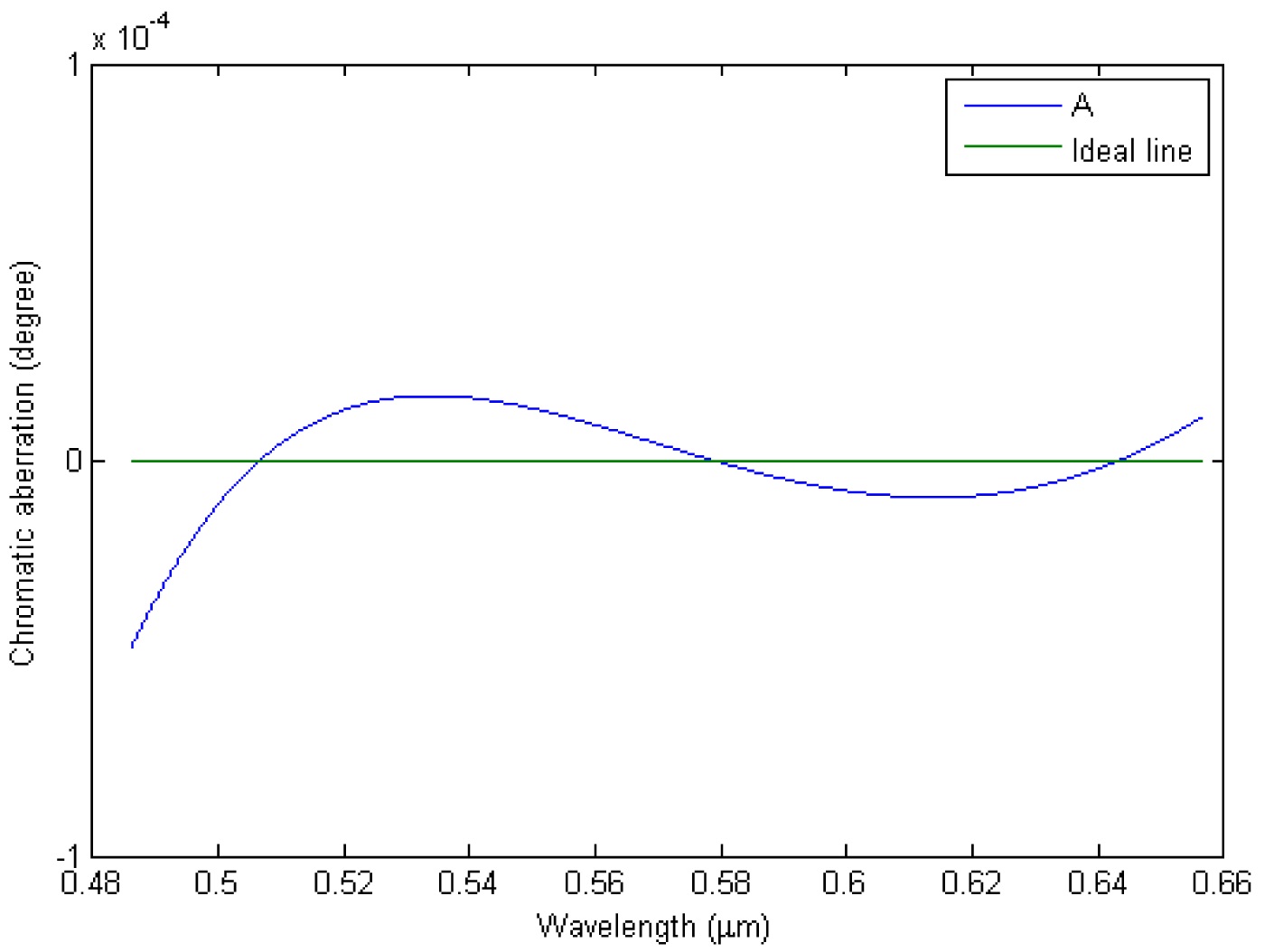
[TABLE 5.] Optimization designs for doublet prisms from group A to group F
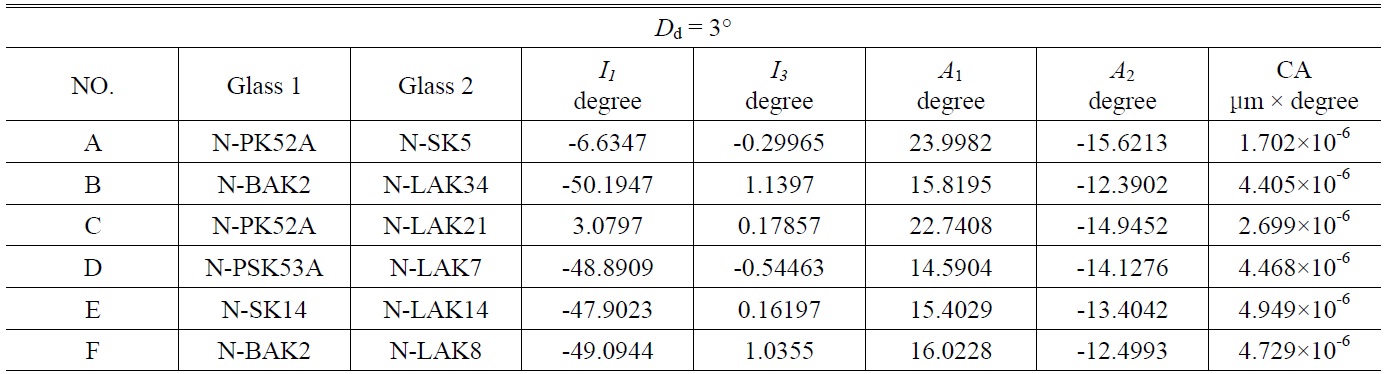
Optimization designs for doublet prisms from group A to group F
results for the optimized designs A to F are listed in Table 5. The chromatic aberration curves A to E corresponding to the optimal designs are shown in Fig. 8. This indicates that the proposed design method is effective in minimizing the chromatic aberration.
A low-cost optimal double-prism method combined with the developed MATLAB program to correct chromatic aberration has been presented. In comparison of the doublet-prism designs shown in Tables 1 and 5, shows that the areas between the paraxial and real chromatic aberration curves are similar. We can quickly find the best combination of doublet prisms by choosing the materials with small differences in relative partial dispersion and large differences in Vd number, and minimizing the real
chromatic aberration of doublet prisms by an optimization program.