Following the widespread use of multicore processors in servers and desktop computers, embedded processors are also increasingly using multicore processors to achieve better performance and energy efficiency. Examples of embedded multicore processors include the dual-core Freescale MPC8641D, the dual-core Broadcom BCM1255, the dual-core PMC-Sierra RM9000x2, the quad-core ARM11 MP-core, and the quad-core Broadcom BCM1455. Real-time systems, ranging from real-time media processing systems to large-scale signal processing systems such as synthetic-aperture radar systems [1], are also expected to benefit from multicore processors.
Different cores often share the last-level cache such as an L2 cache to efficiently exploit the aggregate cache space, because a shared L2 cache makes it easier for multiple cooperative threads to share instructions and data, and to reduce the cache synchronization and coherency costs, which become more expensive in separated L2 caches [2]. However, the shared L2 cache can lead to possible runtime interferences between co-running tasks on different cores. Therefore, the worst-case performance of each task may be significantly degraded. For example, Fedorova et al. [3] found that L2 cache misses can affect the performance of multicore applications to a much larger extent than L1 cache misses or pipeline hazards.
In real-time systems, safely and accurately estimating the worst-case execution time (WCET) of each hard realtime task is crucial for schedulability analysis. However, this is challenging, because the WCET of a task is dependent not only on its own attributes, but also on the timing of the hardware architecture, such as instruction pipelines, caches, or branch predictors. The multicore processors make it even more challenging to obtain WCET, because different tasks running concurrently on different cores may interfere with each other in accessing the shared resources such as the cache. Unfortunately, a majority of research efforts on WCET analysis have been focused on uniprocessors [4], which cannot be directly applied to estimate the WCET for real-time tasks running on multicore processors with shared caches.
In a multicore processor, the WCET of a task is still dependent on other tasks that are running concurrently on other cores, as they have different inter-task cache interferences and thus add different amounts of memory latencies to the total execution time. The existence of such tasks depends on the schedules generated by the scheduler itself. To schedule different tasks, the scheduler needs to know the WCET of each task. Therefore, unlike in a uniprocessor, where the WCET analysis and scheduling can be generally done independently, a multicore processor with shared caches creates a circular interdependence between WCET analysis and real-time scheduling, which is a new research problem that must be solved to enable reliable use of multicore processors for hard real-time systems.
To the best of our knowledge, this paper is the first work to address this circular interdependence problem for hard real-time systems. We propose a heuristic-based strategy that can schedule real-time tasks on a multicore platform correctly and efficiently by breaking the interdependence between WCET analysis and scheduling in a multicore processor. While the proposed approach cannot always generate the optimal results, we hope this paper can provide useful insights for the research community towards solving this challenging problem.
As a first step toward addressing the interdependence between multicore WCET analysis and multicore realtime scheduling, we focus on studying a dual-core architecture where both cores are symmetric, single-threaded, and share an L2 cache. Built on an offline multicore realtime scheduling approach, we propose a heuristic-based method to use the WCET and inter-core cache interference information to safely schedule real-time tasks, while minimizing the worst-case inter-thread interferences in the shared L2 cache and the WCET. The experimental results indicate that the enhanced offline scheduling approach can reduce the utilization as compared to a naive multicore scheduling approach that does not consider the interaction between WCET analysis and multicore real-time scheduling.
The rest of the paper is organized as follows. Section II reviews the background and related work of the multicore real-time scheduling. Section III describes the framework of a multicore real-time scheduler for hard real-time systems. Next, the scheduling approaches with a greedy heuristic are depicted in Section IV. The evaluation methodology is explained in Section V, and the experimental results are presented in Section VI. Section VII presents the conclusion.
Traditionally, there have been two types of scheduling approaches for periodic real-time tasks on multiprocessors: global scheduling [5-8] and partitioning scheduling [9-11]. In the global scheduling, a global scheduler is responsible for scheduling all the eligible tasks among all the processors. The scheduler selects the eligible task with the highest priority from a single priority-ordered queue of real-time tasks. This approach can be implemented based on optimal uniprocessor scheduling algorithms, such as global rate-monotonic (RM) or global earliest deadline first (EDF). However, these approaches may lead to arbitrarily low processor utilization in real-time multiprocessor systems [6]. Another global scheduling approach called proportionate fair (Pfair) scheduling has been proven to produce the only known optimal utilization to schedule periodic tasks on multiprocessors [7,8,12]. However, these global scheduling approaches generally only work well for soft real-time systems.
Another type of scheduling approach is the partitioning- based approaches [9-11]. In partitioning approaches, each task is assigned to one core of the multicore processor before being scheduled, and each core has its own independent scheduler to fulfill the scheduling procedure. The partitioning approaches basically reduce the multiprocessor scheduling problem to a set of uniprocessor scheduling problems. However, there are two obstacles for partitioning approaches. First, it is a bin-packing problem to find an optimal assignment of tasks to processors, which is NP-hard. So, tasks usually have to be partitioned with suboptimal heuristics, such as First Fit Decreasing Utilization (FFDU) [11]. Second, there are some task systems that are schedulable if and only if they are not partitioned.
While traditional scheduling algorithms work very well for uniprocessors, multicore computing brings a new challenge, which is the interdependence between multicore real-time scheduling and WCET analysis of each concurrent real-time task, as mentioned before. Since neither traditional partitioning nor global scheduling approaches consider inter-thread cache interferences on multicore processors, nor the dependence on the schedules generated, the safety and reliability of these scheduling approaches are questionable for hard real-time and safety-critical systems.
Recently, some research efforts have been made for real-time scheduling with multicore processors. Anderson et al. [12] studied cache-aware scheduling to discourage the co-scheduling of tasks, which can worsen the performance of shared caches. A study by the same group showed that it is possible to encourage tasks from the same multithreaded application to share a common working set, which will decrease the inter-thread interferences on the shared L2 cache [13]. In another study a sharedcache aware approach with more complex heuristics was proposed, with real-time tasks scheduled globally according to various scheduling policies, such as the cacheaware policy and the lost-cause policy [14]. It was demonstrated that this shared-cache aware approach can result in better shared cache performance than the global EDF (G-EDF) scheduling approach.
Some recent research works have proposed hybrid approaches that combine elements of both partitioned and global scheduling. Job splitting was proposed in one such study to cater to sporadic task sets with implicit deadlines [15]. Each processor
While these multicore real-time scheduling approaches generally can be very useful for soft real-time systems, they cannot guarantee safety and reliability for hard realtime systems. An important reason is that the metrics such as working sets used in these approaches are based on either profiling or average-case results, which may be quite different from the worst-case performance results. Moreover, these approaches have not considered the circular interdependence between WCET analysis and multicore real-time scheduling. In contrast, our work is based on accurate multicore WCET and inter-thread cache interference analysis, and we propose a greedy algorithm to incorporate multicore WCET analysis results into the scheduling to generate correct schedules while minimizing the inter-thread cache misses.
III. FRAMEWORK OF MULTICORE REAL-TIME SCHEDULING AND OUR ASSUMPTIONS
A periodic task model is considered. In a periodic realtime system, a task T can be characterized by the WCET
Assumptions and Limitations: To reduce the complexity and to focus on the interplay of multicore WCET analysis and scheduling, the following assumptions are made. First, only a simple task model is considered, in which all tasks share a common period and are non-preemptive. Second, to focus on the circular dependence between WCET analysis and scheduling for multicore processors, only the inter-core cache interferences due to instruction accesses are considered. There are also other inter-core interferences in a multicore processor, such as data interferences, shared bus interferences, etc. [20]. Nevertheless, the problem and approaches studied in this paper are independent of the WCET analysis techniques. The proposed methods can also be extended to multicore chips with shared data caches and unified caches if their WCETs can be accurately analyzed. Third, we assume that there is no job preemption, so that no job would migrate between different cores during its execution in the global scheduling. Fourth, we focus on offline scheduling algorithms for hard real-time systems (all the scheduling decisions are made before the execution of the tasks in the offline scheduling), because online scheduling may not guarantee safety, and may also incur excessive runtime overhead due to the circular dependence of WCET on the scheduling itself.
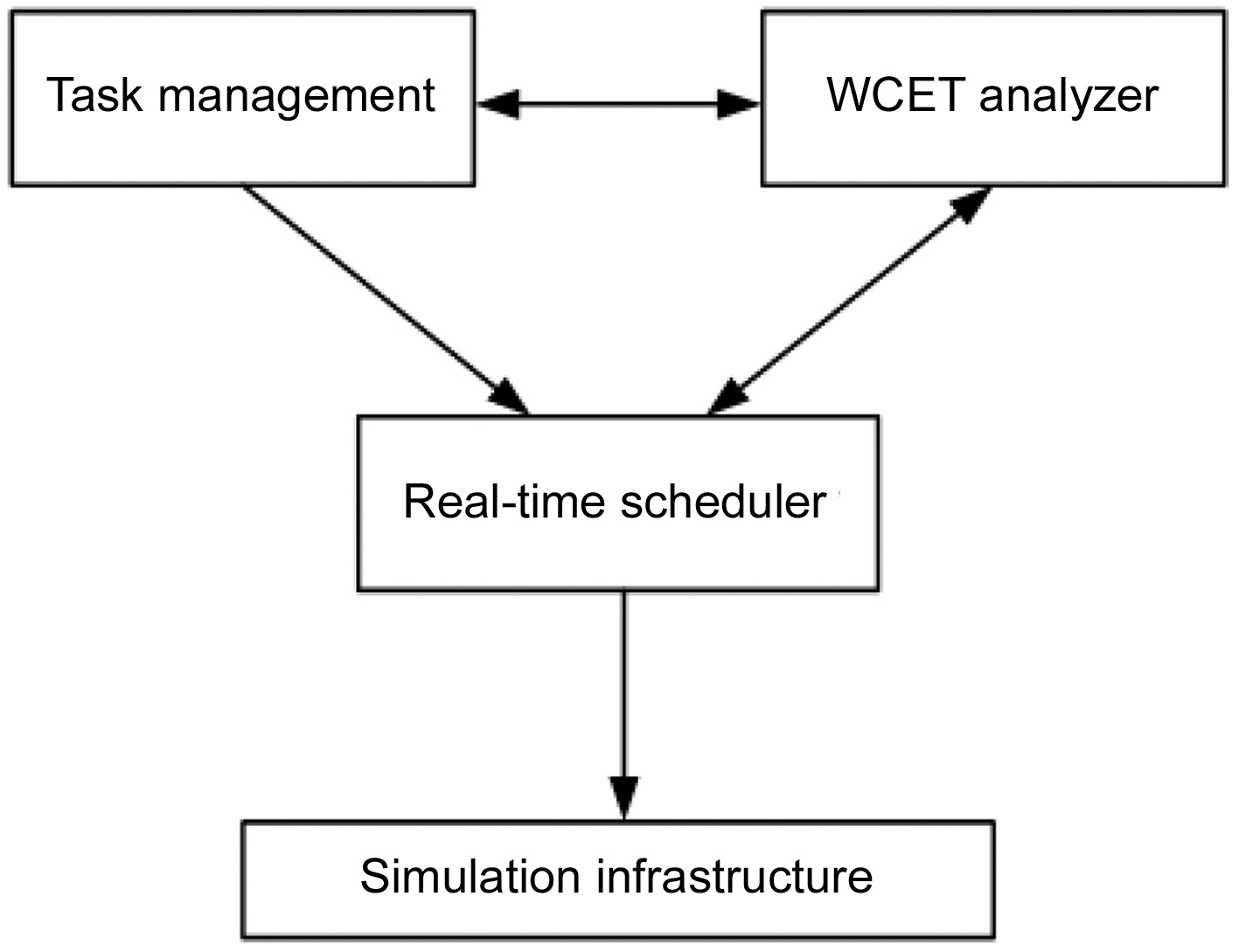
We propose a framework of the multicore real-time scheduling to study and verify the interactions between the multicore real-time scheduling and the inter-thread shared L2 cache interferences. This framework consists of the following components, as demonstrated in Fig. 1.
Task Management: The task manager is responsible
for managing the real-time task sets, including reading the binary code of the input tasks and obtaining their period and WCET parameters on a uniprocessor. It also synchronizes the parameters of computer architecture models among all components, such as the number of cores, cache and memory configurations, and so on.
WCET Analyzer: The WCET analyzer can generate the WCET of a task for both single-core and multicore processors. The estimated WCET is then provided to the Task Management module and the Real-Time Scheduler module.
The multicore WCET analysis method used in this work is based on a fine-grained approach that uses extended integer linear programming (ILP) to model all the possible inter-thread cache conflicts [21]. In this approach, a number of ILP equations and inequalities are generated to model the control flow of the program. ILP equations and inequalities are also generated based on the cache conflict graph of each thread to model the shared L2 instruction cache interferences. The multicore WCET analyzer includes an approach to remove the redundant L2 cache interferences to tighten the WCET analysis. The WCET and inter-thread cache interferences of a dual-core processor with a shared L2 instruction cache can be derived by using an ILP solver to solve the objective function and the generated ILP equations and inequalities. More details of this multicore WCET analysis approach can be found elsewhere [21]. Since our method runs offline, the timing cost of the WCET Analyzer is acceptable, and will not affect the execution of the generated schedules.
Real-Time Scheduler: The real-time scheduler obtains the basic information of the input real-time task set from the Task Management module, and then generates a schedule for the task set on a designated multicore architecture by considering the effects of the inter-thread L2 cache interferences.
Simulation Infrastructure: This infrastructure simulates the execution of the real-time tasks following the scheduling generated by the Real-Time Scheduler module. It can simulate various environments with different numbers of cores and different cache models. It also provides performance statistics to verify the validity and performance of the scheduling algorithm.
The scheduling algorithms presented focus on hard realtime systems. Therefore, the scheduling generated by our multicore scheduling approach must guarantee that all tasks meet their timing constraints, or else the schedule fails. We propose an approach with a greedy scheduling heuristic to generate safe schedules for hard real-time systems, while minimizing the inter-thread shared L2 cache interferences. In our approach, multicore WCET analysis is integrated into the offline multicore scheduling. The proposed approach can be applied to both partitioning scheduling and global scheduling. There are some prerequisites that must be known in our approach, such as the common period of all tasks, the utilization of each task (using the WCET on a single-core processor), the ready time, and the deadlines of all the jobs of each task.
>
A. A Greedy Heuristic to Minimize Inter-Thread L2 Cache Interferences
In principle, it is ideal to find out an optimal schedule that is not only safe, but also leads to the least inter-thread shared L2 cache interferences. The optimal schedule can minimize the total utilization of the tasks and prevent the L2 cache performance from becoming a bottleneck of the system performance. The problem to determine an optimal schedule can be modeled as a combinatorial optimization problem. Specifically, an optimal combinatorial sequence needs to be derived from multiple independent sequences of various sizes. The computational complexity of this combinatorial optimization problem is NP-hard. Even though this problem is constrained to a dual-core system in our study, its computational complexity still increases exponentially with the increase of the number of the jobs to be scheduled. Consequently, a suboptimal solution is adopted by using a greedy heuristic to minimize the inter-thread shared L2 cache interferences. The greedy heuristic called least inter-thread interference to both cores (LIIBC) is described below, which is used to schedule jobs when several are ready at a given clock cycle.
1) If both cores are available, two ready jobs are scheduled to respective cores at this clock cycle, if the corunning of these jobs leads to the least inter-thread shared L2 cache interferences on both cores among all the ready jobs.
2) If only one core is available, a ready job is scheduled to this core at this clock cycle, if its co-running with the job already scheduled on the other core at the same clock cycle leads to the least inter-thread shared L2 cache interferences on both cores among all the ready jobs.
This greedy heuristic is used only for the simplified periodic task model assumed in this paper, in which each task has the same period. For tasks with different periods or priorities, inter-thread cache interferences can be an influencing factor, but not one that uniquely determines the scheduling priority for achieving the best system utilization, which will be studied in future work.
In the partitioning scheme, the scheduler begins with task assignment by the heuristic of FFDU [11]. If the task assignment finishes successfully, the tasks assigned to one core are first scheduled by the clock-driven scheduling algorithm [11]. This core is called the first core, and the other core is called the second core in this paper. The schedule of the tasks assigned to the second core is generated according to the
The inputs of the
In the main procedure of the algorithm, if the ready time of a job is equal to the current clock cycle denoted by
[Table. 4] Algorithm 1 LII_Partitioning_Scheduling

Algorithm 1 LII_Partitioning_Scheduling
(at line 8) is used to check the availability of the second core at the current clock cycle, which checks if the execution of any scheduled job in
Otherwise, a job already scheduled on the first core is identified by the function
The scheduling procedure is repeated for each clock cycle by increasing
In the global scheme, a global schedule is generated for both cores following the
[Table. 5] Algorithm 2 LII_Global_Scheduling

Algorithm 2 LII_Global_Scheduling
The scheduling procedure first adds the jobs to the
The relevant scheduling procedure for only one available core is shown in lines 16 to 31, and consists of four steps. First, a job
If no core is available at the current clock cycle, the algorithm continues to the scheduling procedure for the next clock cycle by increasing
algorithm is terminated if the scheduling procedure fails or
The computational complexity of both scheduling algorithms depends on two factors: the number of scheduling decisions, and the complexity to find the scheduling jobs with the least worst-case inter-thread cache interferences according to the greedy heuristic of LIIBC. Assume that
In the global scheme, as the inter-thread shared L2 cache interferences are computed between any two ready jobs if both cores are free, there are
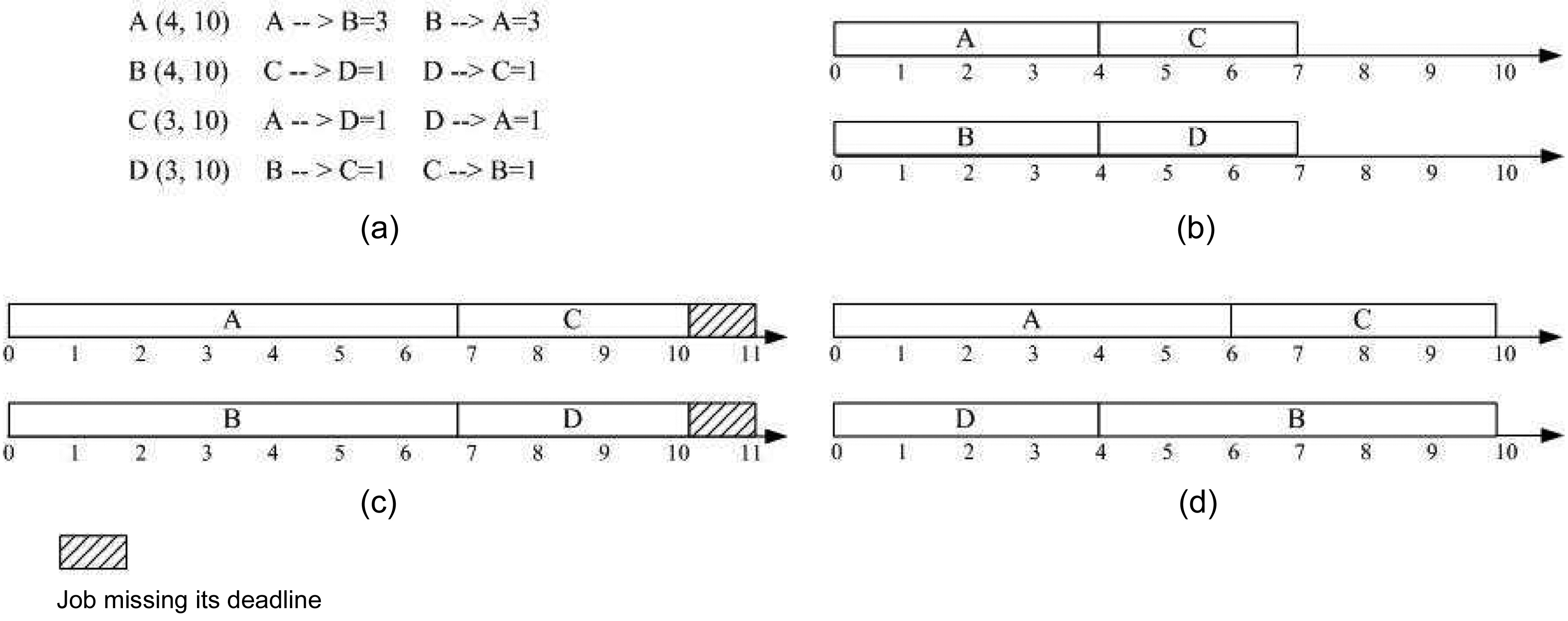
An example of our multicore real-time scheduling approach is demonstrated in Fig. 2. There are four real-time tasks to be scheduled on a dual-core hard real-time system. Fig. 2a shows the deadline and period for each task, as well as the additional execution cycles caused by intertask cache interferences. Fig. 2b shows the result of the original static partition scheduling based on FFDU [16], where tasks A and C are assigned to Core I, and tasks B and D are assigned to Core II. However, it should be noted that the original scheduling does not consider the inter-thread L2 cache interference between these tasks. Consequently, the schedules generated are not safe, because potential inter-core L2 cache conflicts can increase the execution time of the jobs on both cores, which may eventually ruin the “correctness” of the original schedule.
In Fig. 2c, the inter-thread L2 cache interferences are involved in the scheduling process. Since it is based on the original scheduling on both cores, as shown in Fig. 2b, jobs A1 and B1 are co-scheduled to be released at time point (or cycle) 0. With the inter-thread L2 cache interferences taken into account, the end time of jobs A1 and B1 will be extended to time points 5 and 4, respectively. As the deadline of job C1 is at time point 5, the scheduling of C1 after job A1 will make C1 miss its deadline, even though the co-scheduling of jobs C1 and D1 does not lead to any additional inter-thread L2 cache misses. Therefore, the original scheduling approach cannot actually generate a successful scheduling for the target hard real-time system.
A successful scheduling generated by the greedy algorithm to minimize the inter-thread L2 cache interferences in the partitioning scheme is illustrated in Fig. 2d. The initial scheduling on Core I is the same as in Fig. 2b. The scheduling process on Core II begins to check the ready job at time point 0 when there are two ready jobs B1 and D1. The inter-thread cache interferences between jobs B1 and A1 will add two more cycles to their original WCET without considering the inter-thread L2 cache interferences. In contrast, this value is 4 if jobs D1 and A1 are co-scheduled. According to the greedy algorithm based on LIIBC, job D1 is selected to be released at time point 0 together with job A1, which extends the end time of job A1 to time point 4 and extends the end time of job D1 to time point 3. It is clear that job B1 will be released at time point 3, and job C1 will be released at time point 4. As the co-scheduling of B1 and C1 will not bring any additional inter-thread L2 cache interference to job C1, job C1 will meet its deadline at time point 5. So, the release time of C2 can be determined at time point 5, and it can be guaranteed to stop at time point 6. Although job B1 is co-scheduled with jobs A1, C1, and C2, only the coscheduling with job C1 can lead to one more cycle to its original WCET. Therefore, job B1 can stop at time point 6 and meet its deadline.
In case of the global scheme, there are four ready jobs A1, B1, C1, and D1 in the ready job queue at time point 0, and there are no inter-thread L2 cache interferences between C1 and D1. So, jobs C1 and D1 are determined to be released together at time point 0, and their end times are at time points 1 and 2, respectively, as illustrated in Fig. 2e. As only Core I is available at time point 1, only one job can be selected to be released from jobs A1 and B1. The total additional WCET brought about by the coscheduling of jobs D1 and A1 is one cycle; however, this value becomes two in the case of co-scheduling jobs D1 and B1 at time point 1. Therefore, job A1 is released at time point 1 on Core I. Since job D1 terminates at time point 2 and only job B1 exists in the ready job queue at this time point, job B1 is co-scheduled with job A1 from time point 2 on Core II, which leads to the an additional cycle in each of their original WCETs. Consequently, job B1 ends at time point 5, and job C2 will be released at this time point after job B1. Jobs A1 and C2 will both terminate at time point 6, as there is no inter-thread L2 cache interferences between them. It is clear that the scheduling approach minimizing the inter-thread cache interference in the global scheme helps to generate a valid scheduling for this example.
Our multicore scheduling framework is implemented and evaluated in a multicore simulator by extending SimpleScalar [22]. The WCET analyzer consists of a front end and a back end. The front end of the WCET analyzer compiles both task benchmarks into common object file format (COFF) binary code using the GNU Compiler Collection (GCC) compiler, which is targeted to SimpleScalar. Then, it obtains the global control-flow graph (CFG) and related information about the instructions by disassembling the binary code generated. Subsequently, the back end compiler performs static cache analysis [23] with the enhanced extended ILP method [21]. A commercial ILP solver-CPLEX [24] is used to solve the ILP problem to obtain the estimated WCET. The basic configuration of the simulated dual-core processor is shown in Table 1.
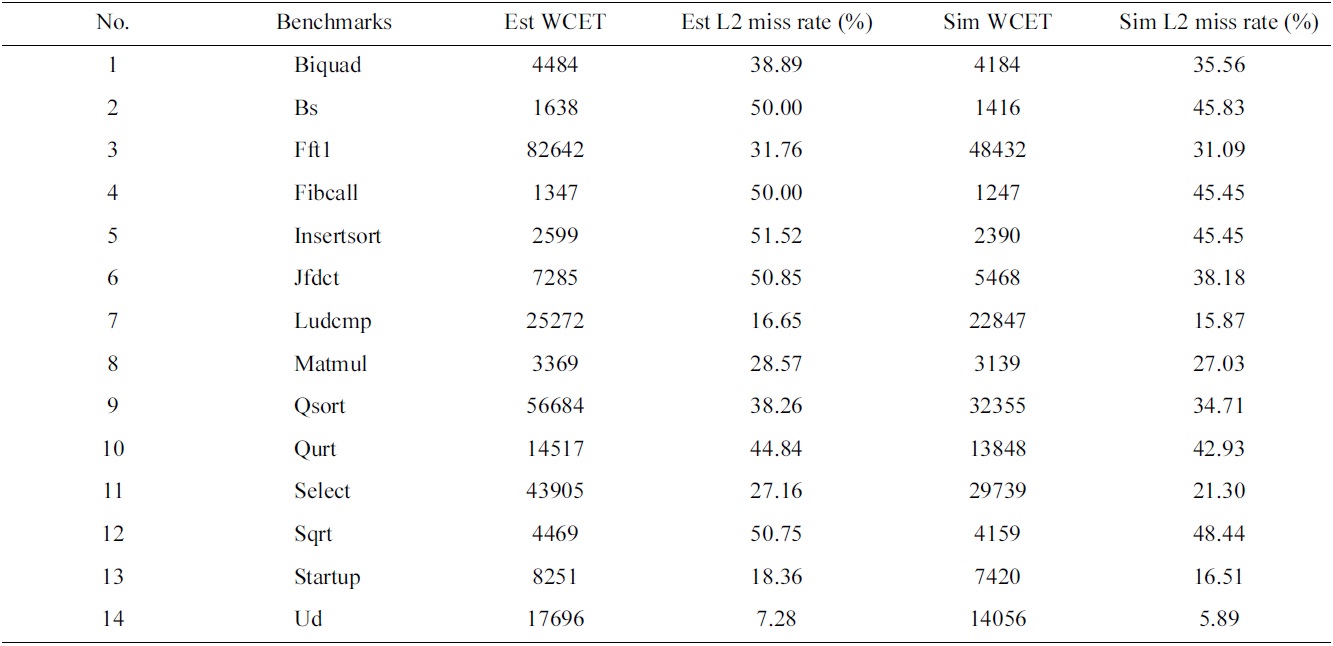
In our experiments, we select fourteen benchmarks from Malardalen WCET benchmark suite [25] as the real-time tasks to be scheduled. The estimated and simulated worstcase performance of these tasks in a uniprocessor is demonstrated in Table 2.
In order to examine the interaction between the interthread L2 cache interferences and the real-time scheduling on a dual-core processor, we use both the utilization defined in Section III and the
45 task sets were designed consisting of the tasks randomly selected from the fourteen real-time benchmarks. The number of tasks in a task set ranges from 4 to 14 to achieve various levels of complexity in the scheduling. These task set instances are scheduled with the following four schemes:
P_Base Scheme: the basic partitioning scheduling approach that first assigns the tasks to each core with the
[Table 1.] Basic configuration of the simulated dual-core processor

Basic configuration of the simulated dual-core processor
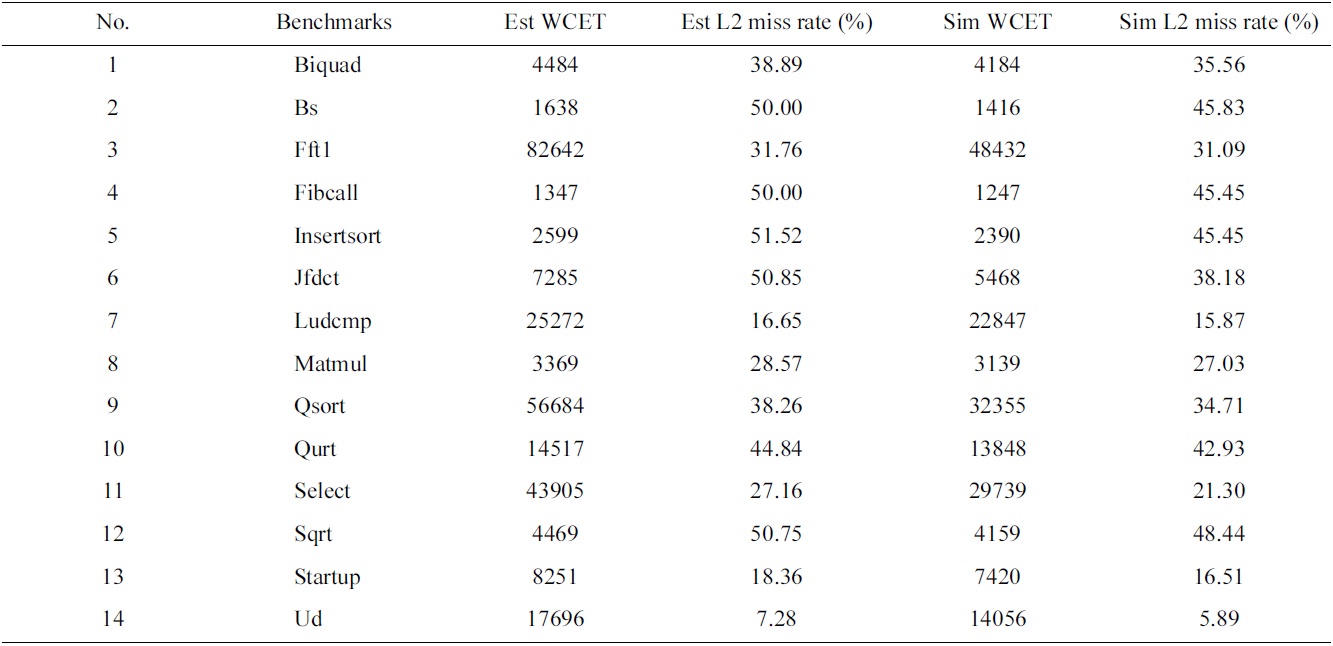
Estimated and observed (through simulation) worst-case execution times (WCETs) and L2 miss rates of the real-time tasks
heuristic of FFDU [11], then the tasks on each core are scheduled by the cyclic scheduling method without considering the inter-thread shared L2 cache interferences. The latencies caused by the inter-thread shared L2 cache interferences are added to the resulting schedule to reflect the actual WCET at runtime.
G_Base Scheme: the basic global scheduling approach that schedules all the tasks to both cores with a global ready job queue by the cyclic scheduling method, which does not consider the inter-thread shared L2 cache interferences. However, the latencies caused by the interthread L2 cache interferences are added to the resulting schedule to reflect the actual WCET at runtime.
P_LII Scheme: the partitioning scheduling approach following the algorithm
G_LII Scheme: this is the global scheduling approach following the algorithm
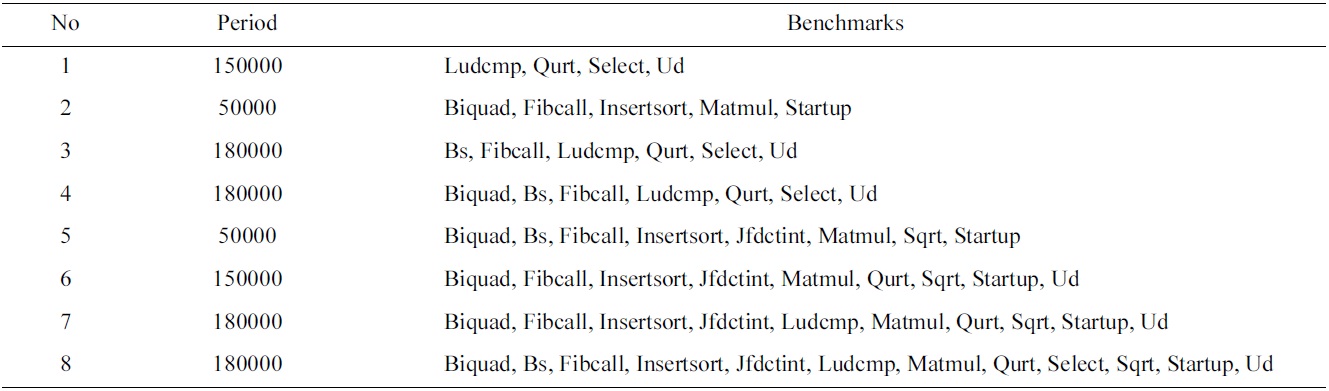
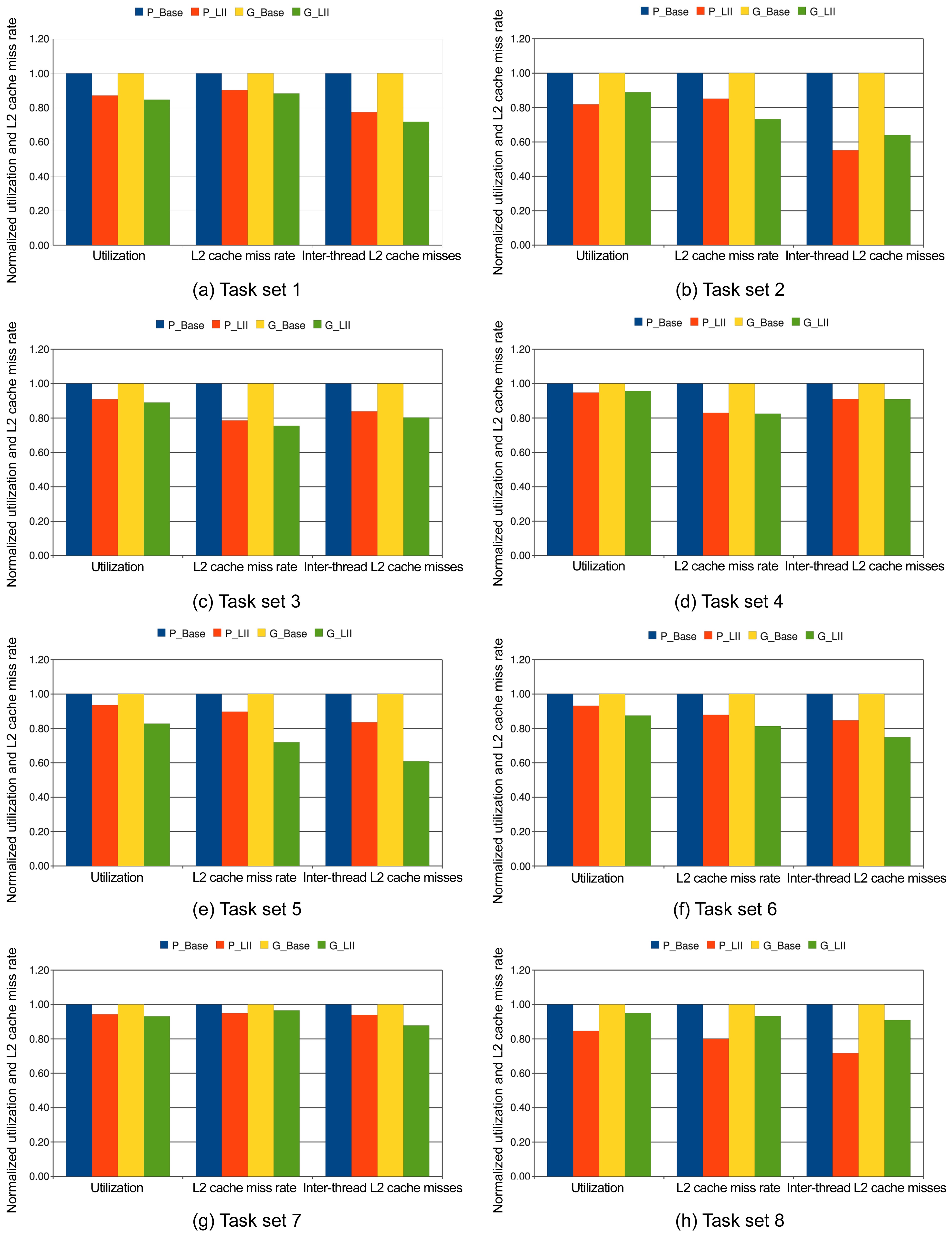
First, we randomly select 8 task sets to be scheduled by all four scheduling schemes, and the number of the tasks in these task sets ranges from 4 to 12, and their common periods vary between 50000 and 180000 cycles, as shown in Table 3. Fig. 3 shows the normalized worst-case utilization, the L2 cache miss rate, and the inter-thread shared L2 cache misses of the P_LII scheme and the G_LII scheme, which are normalized to those of the P_Base scheme and the G_Base scheme, respectively. The utilization, the L2 cache miss rate, and the inter-thread shared L2 cache misses of all 8 of these experiments are lower in the P_LII scheme and the G_LII scheme as compared to the P_Base scheme and the G_Base scheme, respectively. For example, in task set 1, the worst-case utilization, the L2 cache miss rate, and the number of inter-thread shared L2 cache misses in the P_LII scheme are 12.84%, 9.7%, and 22.55% lower than those of the P_Base scheme, respectively. Similarly, the worst-case utilization, the L2 cache miss rate, and the number of inter-thread shared L2 cache misses in the G_LII scheme are 15.28%, 11.67%, and 28.11% lower than those of the G_Base scheme, respectively. The main reason for these results is that since the utilization of a task is determined by its execution cost and period, and its execution cost is supposed to be fixed without considering the inter-thread shared L2 cache interferences, the number of inter-thread shared L2 cache misses that varies with different schedules can become an important factor to determine the total utilization of a schedule for a task set running on a multicore processor. In other words, fewer inter-thread shared L2 cache misses can result in lower execution cost of the jobs scheduled, and decrease the total utilization of the schedule for a task set. Also, the reduction of the interthread shared L2 cache misses may decrease the L2 cache miss rate of the jobs scheduled.
It is well known that the schedulability of a task set can be determined by comparing its total utilization with the system utilization. In principle, if the total utilization of a task set does not exceed the utilization of a system, it is supposed to be able to be scheduled on this system [11].
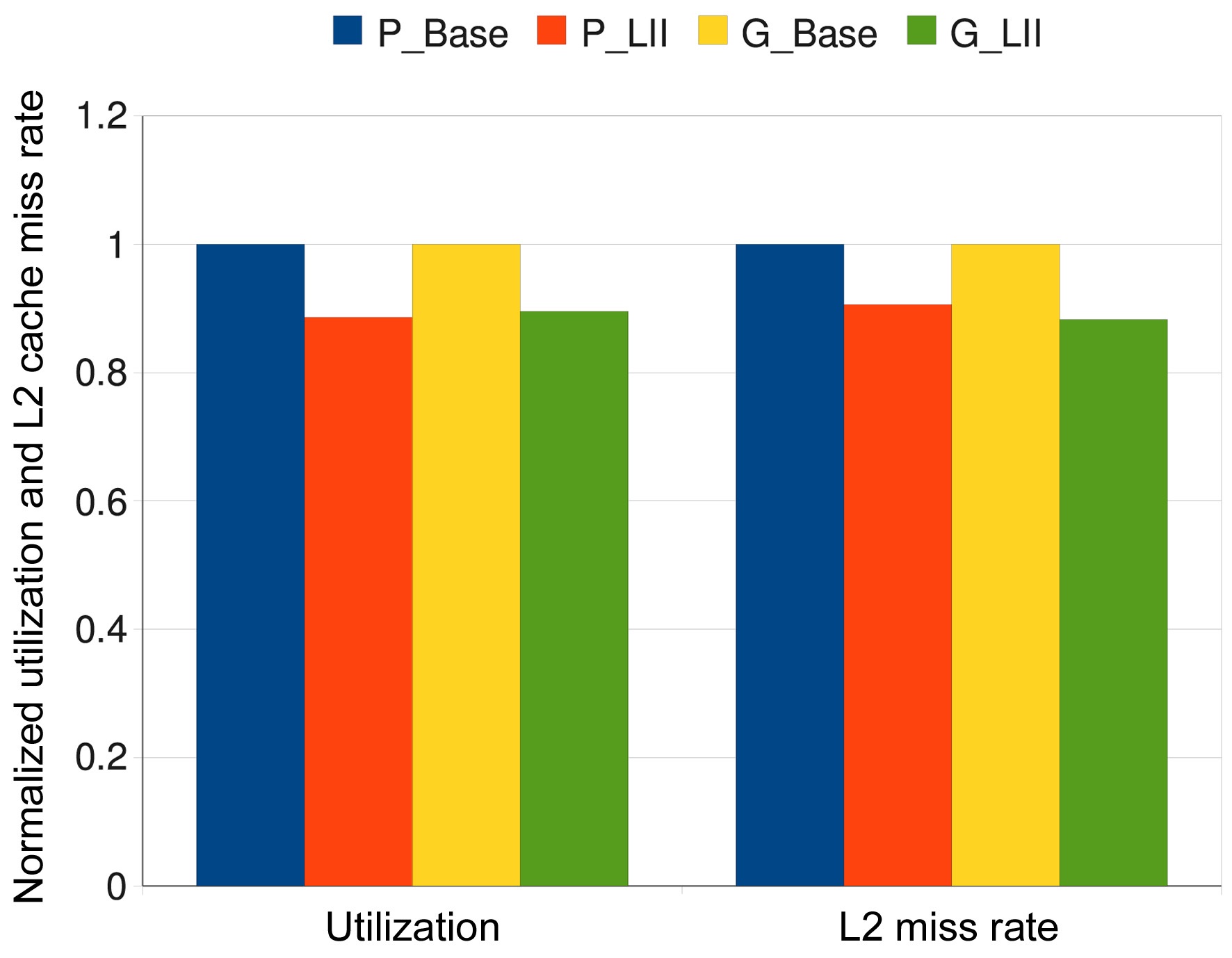
In order to illustrate the generality of our approach, we also apply these four scheduling schemes to the other 37 task sets (besides the 8 task sets listed in Table 3). Fig. 4 shows the estimated worst-case results that are averaged across all these task sets. We observe that the average utilization of the scheduling results of the P_LII scheme are about 11.38% lower than that of the P_Base scheme, while G_LII can reduce the utilization by about 10.46% on average as compared to the G_Base scheme. Also, the
[Table 3.] The benchmarks and periods of the experimental task sets
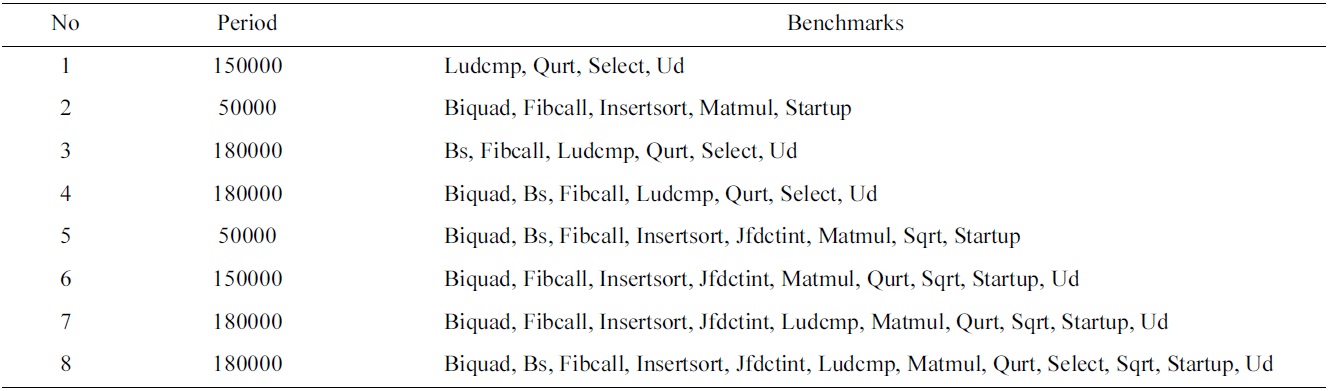
The benchmarks and periods of the experimental task sets
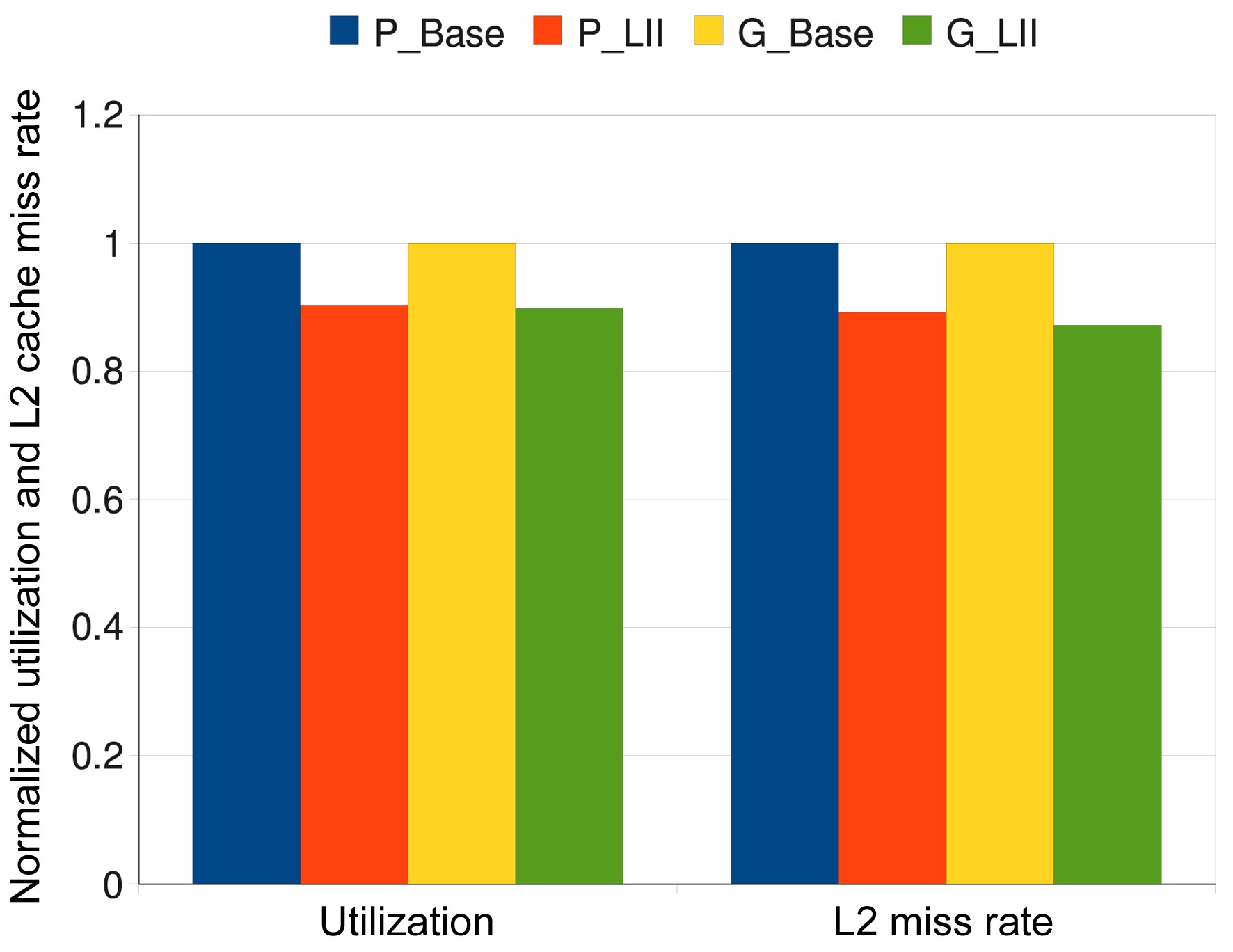
averaged L2 cache miss rate of P_LII scheme is about 9.39% lower than that of the P_Base scheme, and the averaged L2 cache miss rate of the G_LII scheme is about 11.71% lower than that of the G_Base scheme. All these results confirm the advantages of the P_LII scheme and the G_LII scheme. Fig. 5 gives the simulated worstcase results that are averaged across all these 45 task sets, which shows the superiority of the P_LII scheme and the G_LII scheme over the P_Base scheme and the G_Base scheme, respectively.
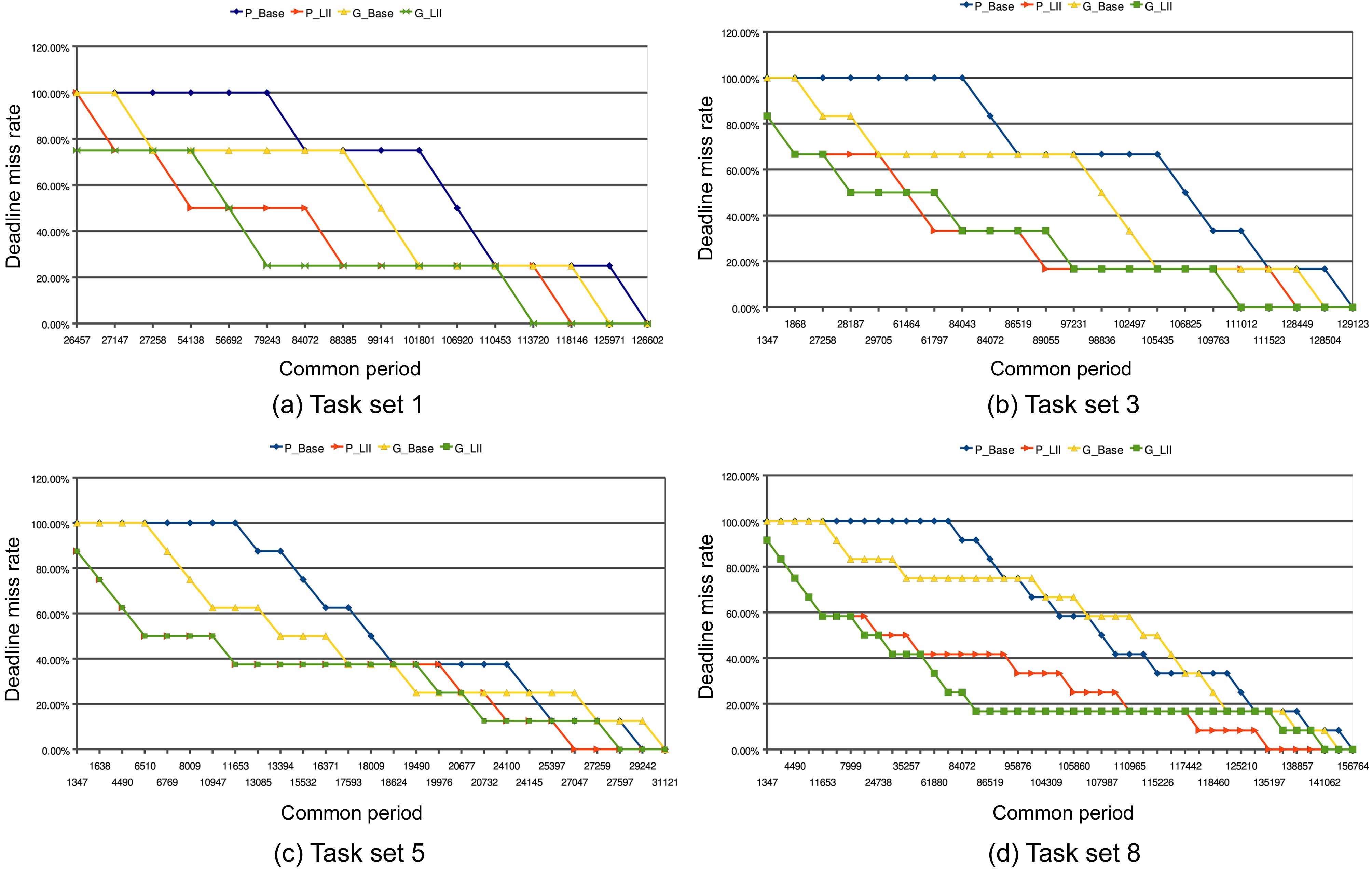
We have also done some experiments to study the impact of various common periods on the deadline miss rate (The deadline miss rate can be defined as the ratio of the number of jobs that cannot meet their respective deadlines to the total number of jobs) of different scheduling algorithms. We randomly choose 4 respective task sets from Table 3, and the deadline miss rates of different schemes with varying periods are illustrated in Fig. 6. In most cases, it is clear that the deadline miss rates in the P_LII scheme and G_LII scheme are less than those in the P_Base scheme and G_Base scheme, respectively, with the same common periods. Taking the case (Fig. 6a) as an example, when the common period is 27147 cycles, the deadline miss rates for the P_LII scheme and G_LII scheme are both 75%. However, the deadline miss rates are still 100% for both the P_Base scheme and the G_Base scheme.
When the common period increases to 84072 cycles, the deadline miss rates for the P_Base scheme and the G_Base scheme are both reduced to 75%. In contrast, the deadline miss rates for the P_LII scheme and the G_LII scheme are both decreased to 25%. Finally, the deadline miss rates for the P_LII scheme and the G_LII scheme become 0% just when the common period grows to 118146 cycles and 113720 cycles, respectively. The deadline miss rates for the P_Base scheme and the G_Base scheme do not become 0% until the common period increases to 126602 cycles and 125971 cycles, respectively. The variation of the deadline miss rates in task sets (Fig. 6b and d) is similar to that of the task set (Fig. 6a).
There is an exceptional case in task set (Fig. 6c), in
which the deadline miss rate for the G_Base scheme is lower than that of the G_LII scheme when the common period ranges between 19490 cycles and 19976 cycles. The main reason lies in that the scheduling algorithm in the G_LII scheme cannot always guarantee that the finishing
time of the scheduling jobs on both cores are earlier than that in the scheduling generated by the G_Base scheme, though it aims to decrease the total utilization of both cores by reducing the inter-thread cache interferences. In this special case, a longer benchmark (i.e.,
The scheduling of real-time tasks in multicore processors with a shared L2 cache can be significantly affected by the inter-thread shared L2 cache interferences, because the WCET of a real-time task can vary significantly due to the inter-thread cache interferences. On the other hand, the inter-thread cache interference and the WCET of a real-time task running on a multicore processor can also be heavily dependent on which tasks are scheduled to run concurrently and when they are started. Consequently, it is important to investigate the interaction between the inter-thread shared L2 cache interferences and the multicore real-time scheduling to safely and efficiently schedule real-time tasks on multicore processors with shared L2 caches. To the best of our knowledge, this has been the first work to take on this challenging problem. We propose a heuristic-based offline scheduling approach that can be applied to both partitioning and global scheduling schemes for multicore processors. The proposed algorithms cannot only minimize the inter-thread shared L2 cache interferences, but also generate a safe scheduling for real-time tasks running on multicore processors.
The experimental results demonstrate that the utilization of the generated schedule is reduced by our approach due to the decrease of the L2 cache miss rate for both the partitioning scheme and the global scheme, because the number of inter-thread cache interferences on a shared L2 cache is reduced. Therefore, the proposed algorithms are likely to generate successful schedules with stricter timing constraints for the task model studied, compared to the traditional scheduling approaches that are not aware of the interdependence between the WCET and scheduling on multicore platforms. Additionally, exploiting the possibly increased slacks is potentially helpful to reduce the power consumption in multicore processors.
In future work, we would like extend the model in this paper to include tasks with different periods and priorities. Relaxed assumptions will also be considered, for example, by allowing job preemption. In addition, we intend to study the inter-core interferences for data accesses as well, and we plan to evaluate the scalability of our approach on processors with more cores, such as 4 cores and 8 cores.