With the bursting growth of the Internet, and the virtually limitless storage space available, there are now hundreds of thousands of items that are available on online stores, whether they be books, movies, or music albums. The shopping experience of a customer has shifted from what was a simple browse-and-search experience among popular items in offline stores, to a search-and-find experience online, with thousands of items. Although this had led to lesser concentrated product sales, with the power of balance shifting from the few best-selling products to niche products that were previously difficult for consumers to discover, a new problem exists: information overload. Paradoxically, now that there are more available items, it has become extremely difficult to discover items that may be of interest to the user.
Recommender systems solve the problem of information overload by filtering unnecessary items, and showing only those that are relevant to the user. Finding items that are relevant to a user or not is determined with user profiles. Among the many existing methods of recommender systems, collaborative filtering is the most effective method, and the most widely used in commercial services. This is because collaborative filtering can be applied to any domain, being independent of the characteristics of the items. It is also relatively easier to implement, compared to content-based and hybrid algorithms, and provides the most satisfying results to users.
However, despite providing the most satisfying results, collaborative filtering does have drawbacks. One of the most notable drawbacks is, at the same time, also the reason why it is able to make relevant recommendations to users: popularity bias. Popularity bias, in which the system becomes skewed towards items that are popular amongst the general user population, makes it near impossible for the system to generate truly novel recommendations. A slightly different problem, but still related to popularity bias, is what is dubbed the ‘Harry Potter’ problem. The extreme popularity of Harry Potter causes it to be purchased with items that are totally unrelated. Once these unrelated co-purchases accumulate, the system detects a correlation between Harry Potter and the unrelated item, mistaking Harry Potter for future recommendations to other users who show interest in the unrelated item. Another serious drawback of collaborative filtering is the cold-start problem, in which the recommender system cannot provide recommendations to a new user, or offer new items as recommendations. The cold-start problem is a serious issue for recommendation systems, as there are hundreds of new users joining, and even more items being added to databases everyday.
In this article, we propose a recommender system based on collaborative filtering and dynamically promoted experts, which can be applied to any domain, focusing on generating novel recommendations, while keeping them relevant. The main contributions of this work can be summarized as follows.
The proposed system tackles the problem of recommendations from a new viewpoint, using the concept of experts and novices among users, and shows the potential of such systems in its ability to deliver novel, yet relevant, recommendations.
The proposed system can act as a solution for popularity bias, while still using collaborative filtering, as it provides recommendations based on seed items that are not similar to the items that are mainly consumed by the user.
The proposed system can also act as a solution to the cold start problem, without the help of content-based recommenders, or any other external information. Because the recommendations are based on experts in certain clusters, users with only a few ratings can be provided with recommendations that are novel and relevant.
Our proposed recommender system utilizes dynamically created experts, who are knowledgeable, not in the entire item domain, but in a smaller sub-domain. This enables fine-grained recommendations that are novel and relevant at the same time.
The proposed system generalizes the key idea of Lee and Lee [1], which was limited to the music domain. With the generalization, the key concepts can be applied to any domain, simply using user ratings.
>
A. Collaborative Filtering-Based Recommender Systems
One of the first recommender systems was Tapestry, which was based on collaborative filtering [2]. Its goal was to tackle the problem of overflowing emails, by filtering out irrelevant ones. Thus, the remaining emails that were delivered to the user would be the essential, relevant emails. In order to achieve this, Tapestry used the opinions of relatively small groups, such as office workgroups, to recognise irrelevant and relevant emails. However, the limitation of Tapestry was that it worked in small networks, due to the fact that users had to be familiar with the preferences of other users.
Another recommender system based on collaborative filtering was a system called GroupLens, by Resnick et al. [3] and Konstan et al. [4]. GroupLens found news articles that were relevant to users, using the key concept that “people who agreed in the past will probably agree again,” and predicted the ratings that the users would give to the news articles. Since GroupLens’ system found similar users based on their past ratings, the users did not need to be aware of the preferences of other users, unlike Tapestry.
Two early examples of recommender systems that analyzed user profiles, or ratings, to filter similar users and generate recommendations, are Ringo and the Bellcore Video recommender. Ringo specialized in music recommendations that were personalized for each user, by using their preferences [5]. Ringo’s recommender system analyzed the ratings each user gave to music artists, and then found similar users to recommend artists to, who were extremely likely of being rated highly by the user. While Ringo focused its recommendations on music artists, Bellcore’s recommender was centered on movies [6]. Similar to Ringo, Bellcore’s recommender system analyzed user ratings to find users with similar profiles, which were then used to produce recommendations.
Among the various collaborative filtering algorithms used in different domains, Amazon.com’s recommender system is one of the most well-known recommenders. While the preceding recommenders used similar users to find relevant recommendations, Amazon.com analyzed item similarities, rather than user similarities. This approach brought many advantages; the main one being that the method was scalable to very large datasets, while still generating extremely relevant recommendations to the user [7].
>
B. Expert-Based Recommender Systems
Amatriain et al. [8] used a collaborative filtering-based approach that used expert opinions crawled from the web. The system used a set of expert neighbors from an independent dataset, whose weights were assigned, depending on their similarities with the user. This method uses actual experts of a domain, which can be an expensive approach, if they need to be found manually.
Kumar and Bhatia [9] propose a community expertbased recommendation (CER) system, which uses an algorithm to find shared interest relationships among people through their blog entries. These people are then grouped, so that those in the same group have similar interests. Next, an expert is chosen from each group, whose blog becomes the only source for generating recommendations. Although this CER system, together with the proposed system by Amatriain et al. [8], may be a solution to the cold-start problem, they both need additional information, such as expert reviews and user blogs. Such drawbacks limit the domains that they can be applied to, and also make it harder to apply to existing recommender systems.
Kim et al. [10] present a recommender system that uses expert groups, who are selected from the user pool, to evaluate Web documents that will be provided to the users. The authority and make-up of these experts depend on user feedback from the Web documents provided to the users. The system performs well when there is an active community of experts evaluating web documents, and active users providing feedback of the retrieved documents. This study by Kim et al. [10] is similar, in that the experts are created dynamically from the user pool. It also can be applied to other domains, other than Web documents. However, the system heavily depends on the feedback that users provide, which is used to improve the quality of experts. Another drawback is that the experts need to examine the contents of the items, when deciding whether it is a relevant recommendation or not. Such examinations are time-consuming, and could be a bottleneck in the performance and scalability of the recommender system.
The basic concept of the system proposed in this paper is to use experts, when providing recommendations to ‘novices’. A broad definition of an expert would be a person who is knowledgeable in a certain area, while a novice is one who lacks such knowledge. Thus, it is only natural that knowledge is transferred from experts to novices. In this regard, we employ users who are considered experts in their domain, to provide recommendations to novices in those domains.
In this recommender system, each user has a domain, in which he or she is a novice, and an expert. An expert is defined as a user whose item consumption is skewed, or focused, on a certain set of similar items. Likewise, a user is a novice in areas where the consumption rate is low. Taking movies as an example, it is only reasonable that a
person who enjoys watching sci-fi movies can provide helpful recommendations to a user who usually watches drama, but occasionally finds some sci-fi movies engaging.
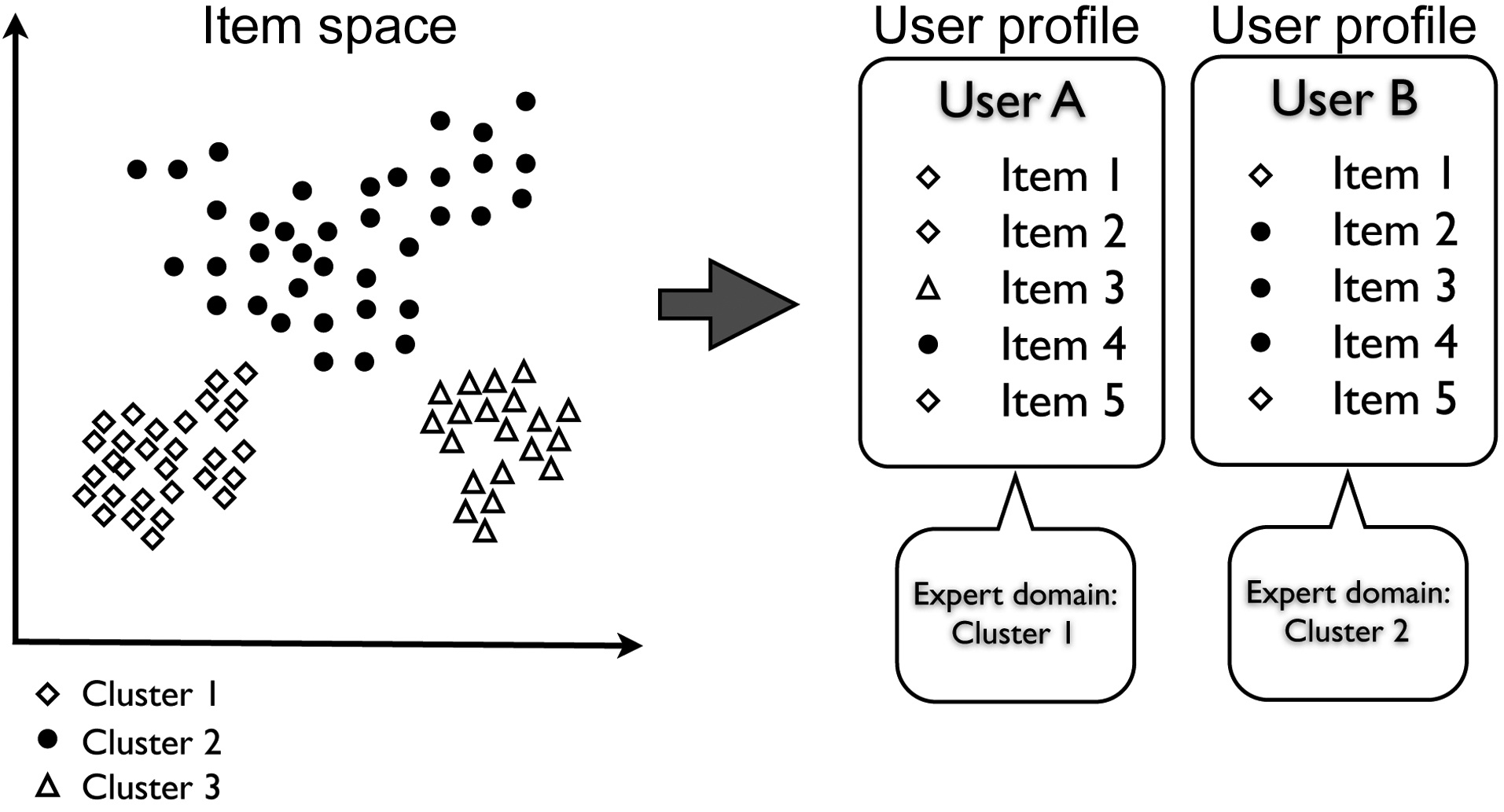
Thus, in order to find experts, the items are placed in an n-dimensional space, so that similar items are placed together, and dissimilar items are apart. Similar items are then clustered, which define the areas that a user can be an expert or novice in. Next, each user is analyzed to see the distribution among the clusters, or areas, that the consumed items are in, and are accordingly labeled as experts for specific clusters, as shown in Fig. 1. When providing recommendations for a novice, the experts of the cluster in which the user is a novice are used to generate novel and relevant recommendations.
IV. DYNAMICALLY PROMOTED EXPERT-BASED RECOMMENDER SYSTEM
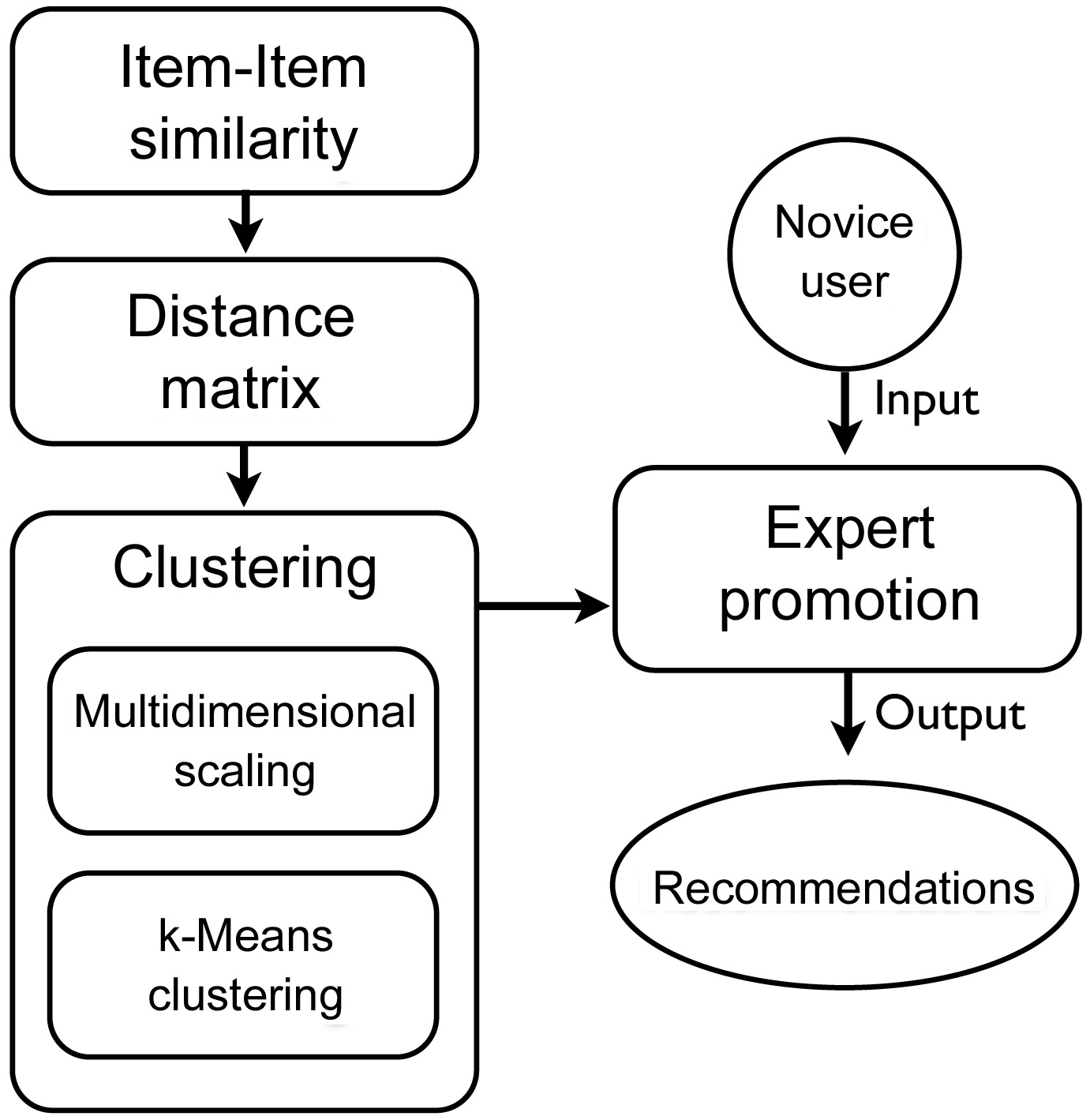
The proposed dynamically promoted expert (DPE)-based recommender system is largely comprised of five steps (Fig. 2), in which the most computationally heavy steps can be processed offline, for better performance. The goal of the five steps is to define experts and novices for a sub-set of items in the entire domain. These experts are then used to generate recommendations for a given novice. In order to achieve this, the entire user-item matrix is used to calculate item-item similarities. Next, the items are projected into an n-dimensional space, so that similar items are close to each other, and dissimilar ones are far apart. This projection of items will create clusters of similar items. Using these clusters, we define an expert to be a user whose profile is concentrated on one of the clusters, making him or her an expert in that cluster. A novice is a user whose profile is concentrated on one cluster, but has few, high-rated items in another cluster, making him or her a novice in the latter cluster. We describe this process in detail in the next sections.
One of the most important steps in collaborative filtering
is computing the similarity between items, given the user-item matrix. The basic idea of computing similarities between any given two items, is to find users who have rated both items, and applying a similarity computation technique to calculate the similarity between the two items. There are many methods of computing the similarity between items, such as cosine similarity, adjusted cosine similarity, and correlation based similarity.
The resulting item-item similarity matrix is similarity values, where the diagonal of the matrix is ones, indicating complete equality and other values ranging from 0 to 1. However, the following step (multidimensional scaling, MDS) requires a distance matrix as input. Thus, the similarity matrix from the previous step needs to be converted into a dissimilarity matrix, or distance matrix. In other words, the values in the similarity matrix need to be inverted, where the diagonal becomes zeros, and the remaining values are converted, to show dissimilarity.
In order to cluster the items, the items first have to be placed in an n-dimensional space. This is done by using MDS, and the item-item distance matrix. Next, similar items are clustered together, using the items that are placed in the n-dimensional space.
1) Multidimensional Scaling
MDS is a set of statistical techniques that are often used in information visualization for exploring the similarities or dissimilarities in data. An MDS algorithm, given a distance matrix between items, assigns a location to each item in an n-dimensional space, while preserving their distances according to the distance matrix. Thus, in our proposed system, MDS is used for its ability to calculate locations for each item in a pre-defined dimension, while minimizing the error of their distances.
2) Clustering
Once the items are scattered in a given space, the next step is to cluster items, so that similar, or nearby, items are clustered together. While there exist many clustering algorithms, the k-means clustering algorithm is used in the proposed system, because of its simplicity and effectiveness.
>
D. Finding Experts for Clusters
Now that every item belongs in a certain cluster, and that these clusters contain similar items, the next step is to assign every user to a cluster, if the users qualify. An assignment to a cluster will indicate that a user is considered an expert for that specific cluster only. For each user, we first analyze the history of rated items, and see where these items lie in the n-dimensional space, which was the output from the MDS stage. If the majority of the distribution of the user’s items lies in a certain cluster, then that user is considered an expert for that cluster. At the same time, the user is considered to be a novice in the clusters to which the remaining minority items belong. Deciding whether the majority distribution of the user’s items lies in a certain cluster, is done based on the Shannon entropy of the items. If the association of each item to a cluster in the user’s history has low entropy, the user is considered to be an expert in the most populated cluster.
>
E. Generating Recommendations
The direction or flow of recommendations goes from experts to novices. Since the previous step analyzed the entire user database, the system simply looks up which cluster a given user is a novice in. Next, the experts of that particular cluster are isolated, and then analyzed to generate recommendations to the novice. In this proposed system, a simple method of using concurring items amongst the experts for recommendations was used.
The proposed recommender system has many parameters that greatly affect the resulting recommendations. The available parameters are as follows.
1) Item similarity computation method:
Adjusted cosine similarity. Item-item similarity can be computed using cosine-based similarity, Pearson correlation, adjusted cosine-based similarity, etc. Among the many available methods, we use the adjusted cosine similarity in this paper.
2) Number of dimensions to use for MDS:
Various dimensions. In this experiment, we test various dimensions to see the effects it has over the produced recommendations.
3) Clustering algorithm:
k-means clustering. Clustering can be done using algorithms, such as linkage clustering, k-means clustering, and expectation-maximization (EM) clustering. In this experiment, we use the k-means clustering algorithm, because of its simplicity and effectiveness.
4) Number of clusters to use for clustering:
Various numbers of clusters. In this experiment, we test with various numbers of clusters, to see the effects they have over the produced recommendations.
5) Qualification of an expert:
Entropy. In this experiment, a user was eligible as an expert, if his or her entropy was lower than 3.9442.
Min. number of items in expert area. A user was eligible as an expert if he or she had at least [Numberofclusters/5] items in his or her expert cluster.
Item ratings of expert cluster. The average rating of items in the expert cluster of the user has to be greater than the average rating of all the items of the user.
The proposed recommender system was experimented on the MovieLens 1 M dataset, which contains 1,000,209 anonymous ratings of approximately 3,900 movies, made by 6,040 MovieLens users (available at http://www.grouplens.org/node/73).
The user ratings were randomly split into two partitions with a 20% to 80% split ratio. The system was built using 80% of the ratings. Although the aim of the recommender is not to predict items from the 20% split, we had to proceed with the experiment this way because of the evaluation metric that we would be using, which will be discussed in the next section.
VI. EVALUATION OF NOVELTY IN RECOMMENDER SYSTEMS
>
A. Issues in Evaluating Novelty
There are numerous ways to evaluate recommender systems, most of them focusing on accuracy metrics. While accuracy metrics are able to evaluate a recommender to some extent, there are crucial limitations that arise, because of the differences in how the user perceives the actual recommendations, and how the metric evaluates them [11]. With any existing metric, it is virtually impossible to know which items are actually novel to the user, and the novelty can only be speculated on, indirectly.
The bottom line is that the best method in evaluating recommender systems, especially when the recommender system focuses on novelty, is to carry out live user tests. However, this seemed difficult to carry out using the MovieLens dataset, which is not a ‘live’ dataset, but an archived one for research purposes, which contains movies from the 1990s. In addition, there is no user pool to begin the experiment, meaning that new users have to be invited in, and user profiles have to be accumulated, before carrying out user studies.
>
B. Novelty Metric for Recommender Systems
Thus, in order to evaluate our proposed recommender system, we use a novelty metric proposed by Vargas and Castells [12], which uses both rank and relevance. We use two metrics that are introduced in the paper, which focus on novelty: the expected popularity complement (EPC), and the expected profile distance (EPD).
To explain the metrics briefly, EPC is a metric that measures the ability of a system to recommend relevant items that reside in the long-tail
where,
EPD, on the other hand, is a distance-based novelty measure, which looks at distances between the items in the user’s profile and the recommended items, as in the following equation
where,
The system was evaluated a total of five times, with slight modifications to the parameters on each iteration. The modified algorithms were as follows:
No modifications (NM): The basic algorithm as explained in Section IV, and using parameters as in Section V, with the exception of omitting the second requirement in promoting experts (i.e., minimum number of consumed items in expert area).
NM + genre vectors (Mod1): The output of the MDS algorithms are coordinates in k-dimensions for each item. In order to spread the items out further in the space, we add additional 18 dimensions, in which the values are either 0 or 1. Each dimension represents a genre in the MovieLens dataset, which is given a value of 1 if the item falls under that genre.
NM + minimum movie consumption (Mod2): This algorithm is the same as NM, but this time includes the second requirement in promoting experts (i.e., minimum number of consumed items in expert area).
NM + remove popular cluster (Mod3): We found that the distribution of experts is usually biased to one cluster. Here, we do not provide recommendations to novices who are a novice in a cluster that has the most number of experts.
Hybrid: This modification of the recommender system is a combination of all the above (i.e., NM + Mod1 + Mod2 + Mod3).
First, we compared the EPC and EPD values of our proposed system with the different diversifications of the matrix factorization (MF) baseline recommender, whose results are presented in the study by Vargas and Castells [12]. The recommendation list was cutoff at the top 50 recommendations, and the discount function
We see that the proposed DPE-based recommender system outperforms the MF baseline recommender and its variations, from the perspective of the EPC metric. Although the proposed system does not aim to generate recommendations with items in the long-tail, it seems that it is able to provide recommendations, while avoiding the most popular items, as can be seen with the EPC values for both ‘Relevance’ and ‘No relevance’. Also, we see that the scores of the variations of the DPE-based recommender system do not change significantly, but see that each modification does improve the recommendations, albeit slightly. Surprisingly, the combination of all the variations of the DPE-based recommender system (i.e., Mod4) actually receives a significantly lower score, compared to individual variations. We speculate that the recommender sees a loss in performance, because Mod4 introduces too many constraints that begin to hinder the recommendations. The constraint with the most impact on the loss of performance may be the experts. Such constraints result in fewer experts, and with fewer experts, it is difficult to find concurring items with confidence.
Switching our perspective to the EPD metric, we observe that for ‘No relevance’, random recommendations score highest in the metric. However, the proposed DPE-based recommender system does not perform as well, receiving values of about 0.56. In the case of ‘Relevance’, the proposed
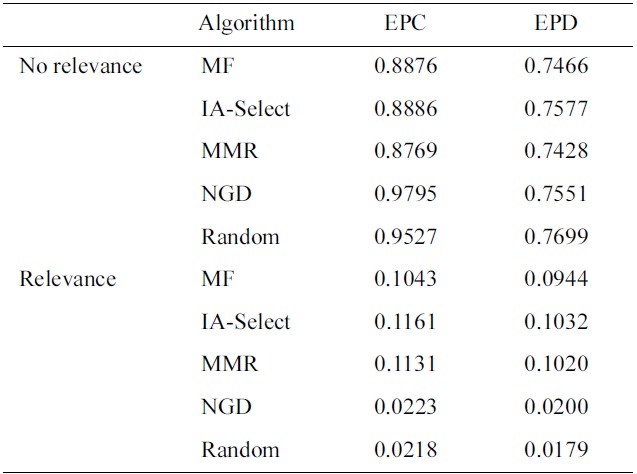
Results on EPC and EPD on different diversification of the MF baseline recommender, with discount function of 0.85k and recommendation list cutoff at 50 (Results adapted from [12])
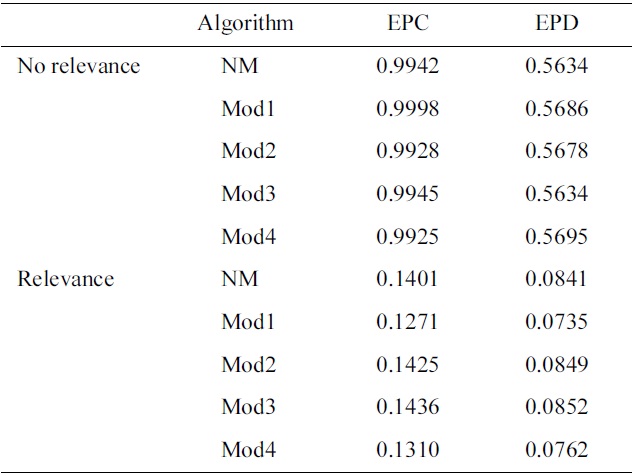
Results on EPC and EPD on different diversification of the proposed recommender, with discount function of 0.85k and recommendation list cutoff at 50
system performs significantly better than noveltybased greedy diversification algorithm (NGD) and random, but falls short of the performance of MF and its variations. The reason why the proposed system does not perform well according to the EPD metric, is that the EPD metric scores relevancy using the hidden 20% split rating data. In other words, an item in the final recommendation list is relevant, only if it exists in the hidden 20% of the user’s ratings. When it does exist, the relevancy score is exponentially proportional to the item’s
rating from the user. The recommendations of the proposed system are generated by analyzing the user’s profile, and finding his or her novice area. Earlier, we had defined a novice area as a cluster of items that the user does not frequently interact with. Hence, while we are generating recommendations from this cluster, it will be extremely difficult to find items in the hidden 20% of the ratings.
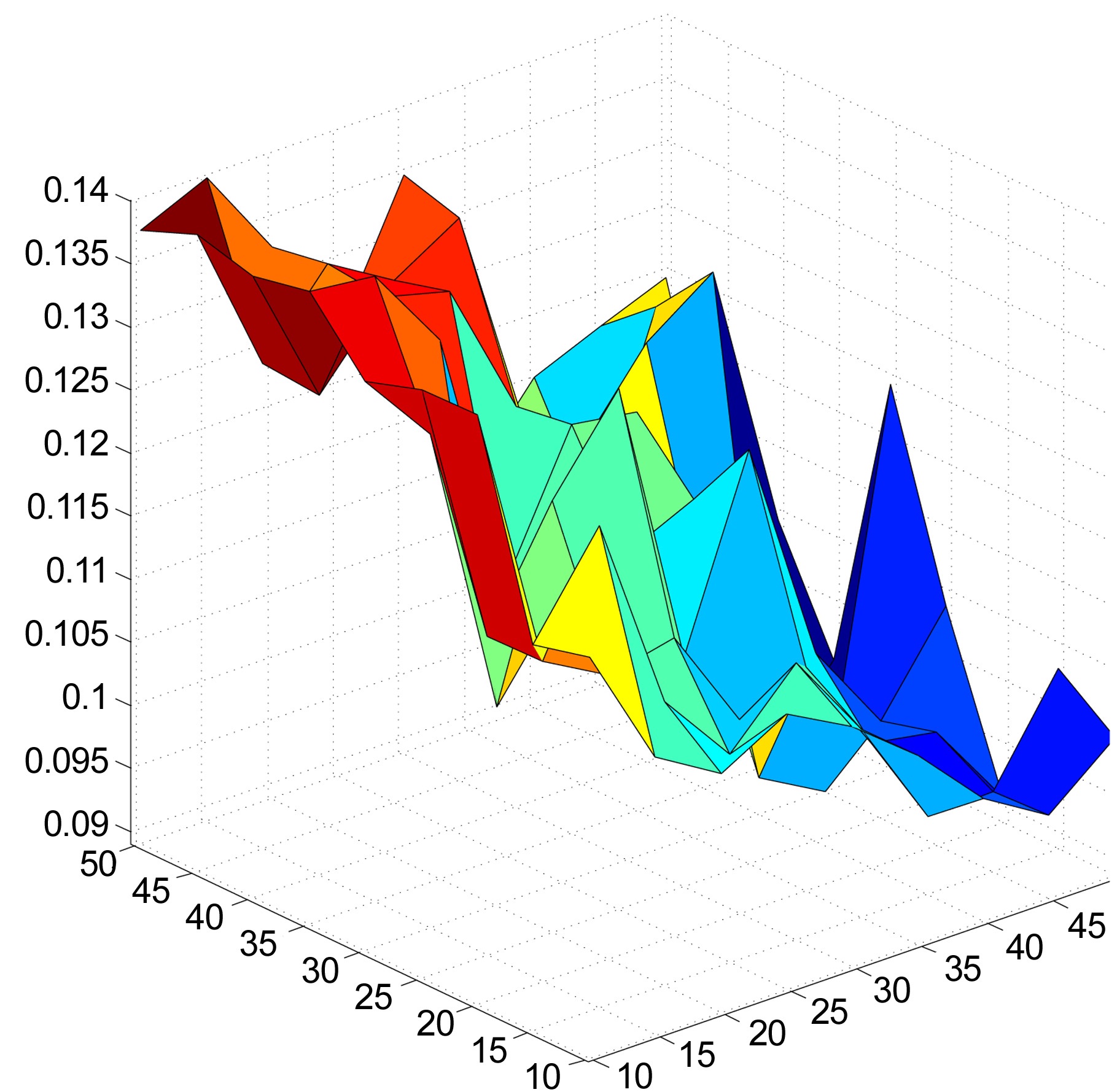
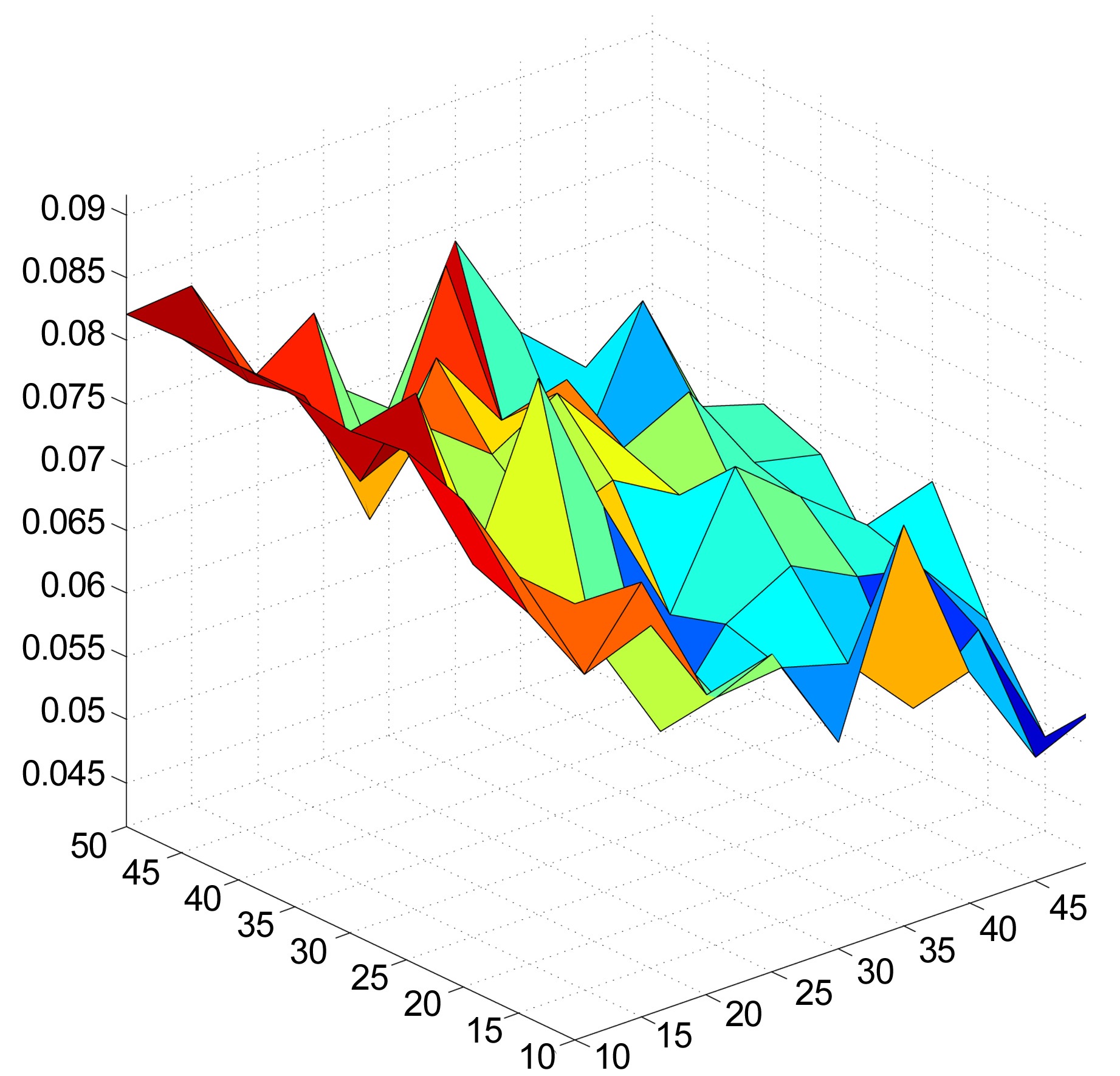
The recommender system was also evaluated, using different combinations of numbers of dimensions and clusters. The numbers of dimensions and clusters ranged from 10 to 50, in increments of 5. Figs. 3 and 4 show that the system scores better for both EPC and EPD metrics, as the number of dimensions increases. On the other hand, increasing the number of clusters results in a loss of performance. We also observe that the increases in EPC and EPD values, when increasing the number of dimensions and keeping the number of clusters low, are not drastic, but still show noticeable improvements.
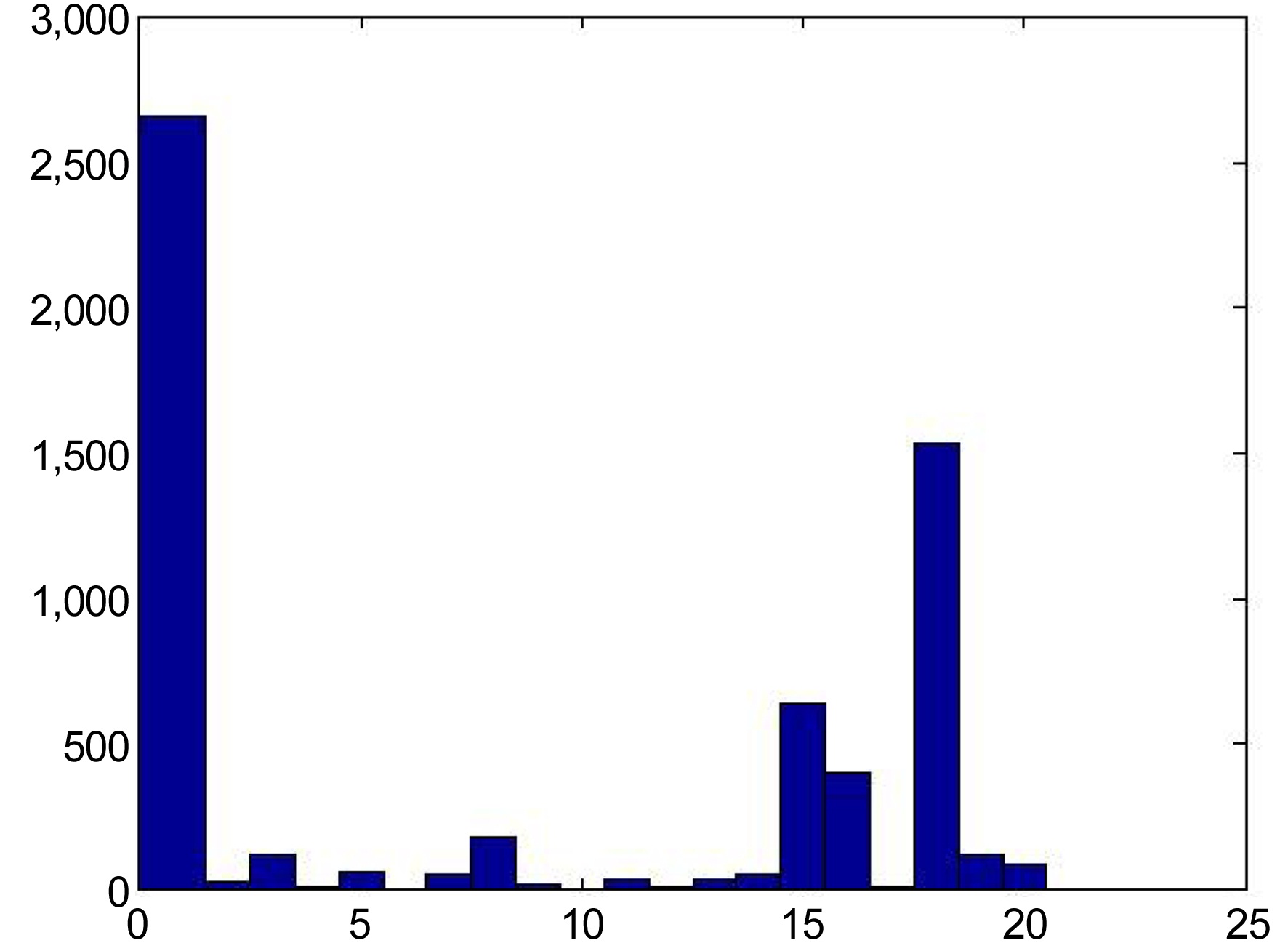
Fig. 5 shows the distribution of entropy among the users. More than half the population of users have entropy values larger than 4. By selecting only users that have entropy values less than 3.94, we are able to select users who show patterns of consuming similar items (i.e., from the same cluster) frequently, while remaining significantly less active in other items and clusters.
Fig. 6 shows an example of the distribution of promoted experts among the available clusters in the item space. One cluster is heavily populated with experts, while the remaining clusters have significantly fewer numbers. This can be observed independently of the number of dimensions and clusters. A similar observation is made in research by Connor and Herlocker [13], where they clustered movies together, and found that the movie distributions were focused on a few clusters. Although it may be unnatural for experts to have a uniform distribution among the clusters, it certainly would be better than having experts focused on a single cluster. One solution may be in finding a clustering algorithm that can create clusters of fairly equal sizes.
VIII. CONCLUSION AND FUTURE WORK
In this paper, we proposed a collaborative filteringbased approach that used dynamically promoted experts among the user pool to generate recommendations. These recommendations were more focused on novelty, while still maintaining their relevance. This was done by creating clusters of similar items, which would act as areas of expertise that the users could be experts on. The proposed system was implemented using movie rating data from the MovieLens 1 M dataset, and evaluated using a novelty metric that took into consideration rank and relevance. We used two different approaches in measuring novelty, EPC and EPD metrics, in which the system performed well with the EPC metric, but did not perform up to par with the EPD metric.
The proposed DPE-based system has many parameters that can greatly influence the outcome of the generated recommendations. In this paper, we examined the changes in performance according to the novelty metrics, for different combinations of dimensions and clusters. Future work will examine the effects of different clustering algorithms, changing the parameters regarding the qualification of experts, etc. A deeper study could include the optimal parameter settings and optimal algorithm selections for specific domains, as the characteristics or consumption patterns of the items may be different for various domains.
However, the most important future work should be a live user test, in order to obtain direct user feedback, as this particular recommender system focuses on providing novel recommendations, while also keeping them relevant. The EPC and EPD metrics were not the optimal metrics to evaluate this system, as the goal of the recommender system and the assessment criteria of these metrics were not in sync. While a live user test may not be easy using the MovieLens dataset, as the data is very old, and users are ‘offline’, it will be possible to do a live user evaluation using other datasets.
![Results on EPC and EPD on different diversification of the MF baseline recommender, with discount function of 0.85k and recommendation list cutoff at 50 (Results adapted from [12])](http://oak.go.kr/repository/journal/11980/E1EIKI_2013_v7n1_21_t001.jpg)