Because of the importance of small target detection in infrared images, many studies have been carried out in this area. Some of the techniques used to estimate a background and obtain the target location include a linear diffusion filter, anisotropic diffusion filter [1], maximum likelihood filter [2], mean shift filter [3], and two-dimensional LMS (TDLMS) filter [4]. It is very difficult to detect a small target in infrared still images with a complex background because of the irregular noises and low SNR [5]. Any effort to detect a small target in infrared still images with a marine background inevitably faces some limitations since clouds or waves are included and appear with a strong noise. Research has been conducted on tracing a target in serial images with the target location obtained in still images in order to resolve such noises [6-9]. This research employed conventional tracing techniques to take advantage of noise irregularity in serial images including a Kalman filter [10], extended Kalman filter [11], and particle filter [12]. These algorithms demonstrate excellent performance in real-time tracing but have some limitations with the application to image processing due to the weak associations among targets in serial images with noises and background interference. Some methods can be used to resolve those problems such as the Probabilistic Multiple Hypothetic Tracking (PMHT) [13] algorithm and the mean shift algorithm [14]. The PMHT algorithm tracks a target by associating small targets in serial images based on the EM algorithm [15] and has a disadvantage of requiring preliminary information on the number of targets. Research has been carried out to help to overcome the disadvantage [16]. The mean shift algorithm is a powerful method used to find extreme values in the dense distribution of data sets, demonstrating great performance in moving nonlinear targets and powerful associations among targets in serial images. However, it also has some disadvantages including requiring early information on targets and research in the case of target appearance and disappearance. This study proposes an algorithm to track multiple small moving targets even in the case of target disappearance and appearance in serial infrared images in an environment with many noises by using a Kalman filter and mean shift algorithm.

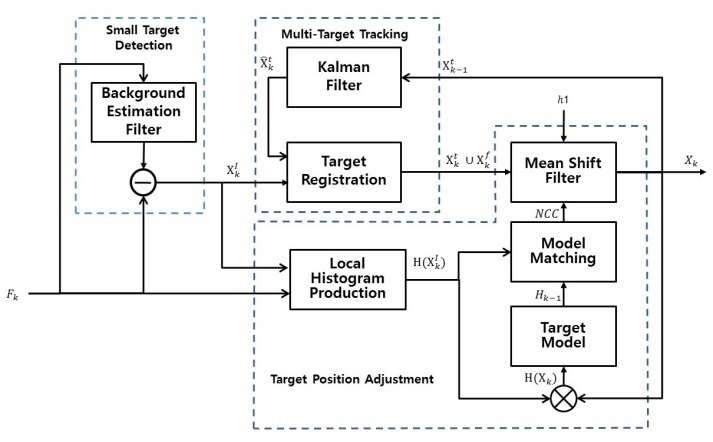
Target detection in still images has a limitation of increasing errors detected when the image has many clutters. Such a limitation is resolved by using the non-uniformity of noise information, which includes location, shape, and brightness, in serial images as important information for target detection. Figure 1 shows the system flow chart of the proposed multiple target tracking technique. F refers to an input image, k is the time index, X ^I is the location of a target detected in a still image, X ^f is the location of a target being newly tracked, X ^t is the location of a target that has been tracked, and H is the histogram model information. The proposed systems can be categorized into three stages: the first stage detects the locations of candidate targets in still images, including small target detection and background estimation filter blocks; the second stage classifies target candidates according to noises or targets by estimating and comparing target locations with a Kalman filter, including multi-target tracking, target selection, and target position prediction blocks; and the final stage fine-tunes each target location in serial images with NCC model matching and mean shift algorithm, including target position adjustment, local histogram production, target model update, NCC model matching, and mean shift adjustment blocks.

The study first estimated image backgrounds in order to detect small targets in still infrared images in a much cluttered environment by introducing and utilizing the existing filters. The study applied and compared several filters including a linear diffusion filter, anisotropic diffusion filter, maximum likelihood filter, mean shift filter, and 2D LMS filter to background estimation, assessing their performance. The filter with the highest performance was used to detect candidate targets in a frame for multiple target tracking.

2.1.1 Linear diffusion filter

A linear diffusion filter determines a pixel value by combining surrounding pixel values linearly. When filtered and processed in such a way, images become blurry as if a low pass filter had been used. The diffusion equation of a linear diffusion filter is shown in equation (1):

f(x,y,t) is the number of inputs repeated, and t is the number of diffusion repeated. The linear diffusion filter based on the discrete expression of equation (1) has the following equation (2):

where N is the neighbor of (x,y), f ⁿ⁺¹ (x,y) is a diffusion image, and f ⁿ (x,y) is an input image. The f ⁿ⁺¹ (x,y) of a diffusion image is obtained by combining the current pixels and their surrounding pixels.

2.1.2 Anisotropic diffusion filter

An anisotropic diffusion filter varies the filtering degrees of targets and backgrounds as a nonlinear filter to avoid the local, blurry problems of a linear diffusion filter. An anisotropic diffusion equation is expressed in equation (3):

where f(x,y,t) is a parameter to determine input reckoning; t is a parameter to determine diffusion reckoning; ∇f(x,y,t) is an inclination according to directions; and c(l) a weighting function. They are defined as shown in equation (4):

This is a decreasing function with c(l) converging toward 0 when l increasing to infinity. When the inclination becomes large, diffusion ceases. An anisotropic diffusion equation can be expressed in a discrete equation (5):

Here, f ⁿ⁺¹ (x,y) is a diffusion image and f ⁿ (x,y) is an input image.

2.1.3 Maximum likelihood filter

A maximum likelihood filter estimates a parameter with some samples and uses it for image segmentation. The pixels of segmented images are used to determine the mean value of each area. A likelihood function to estimate a parameter is shown in equation (6):

Equation (6) is used to estimate a parameter, which is, in turn, used to segment areas according to the classes of which the likelihood functions are a maximum. The means of segmented areas are obtained as in equation (7):

where N_Sk is the number of pixels in each class and S_k represents a segmented class. The pixels of the resulting images are determined with the means of segmented areas to estimate a background.

2.1.4 Mean shift filter

A mean shift filter calculates a mean shift vector to obtain the mean locations of pixels that have a similar brightness distribution A mean shift filter evens out the brightness values while conserving the image boundaries. The mean shift vectors of pixel values are calculated as shown in equation (8):

where x_m, y_m are the mean shift vectors; w is a weight; f is a Kernel function; l is the brightness value of (i,j); and N is a window size. The mean locations shift according to such mean shift vectors. Repetition continues until the mean locations converge and are then replaced with the mean brightness value in the areas with the same convergence locations as those of the mean shift vectors.

2.1.5 2D LMS filter

A 2D LMS(TDLMS) filter is an extended version used to process first-dimensional LMS in a two-dimensional image. Such an s filter predicts the pixels of the resulting images based on the window weights. Errors are calculated by comparing the predicted pixels with the desired results as in equation (9):

where d(x,y) is the desired result, and f(x,y) is the predicted result. A TDLMS filter ensures that the square value of the errors obtained in equation (9) will be a minimum. The weights that should be adjusted for updating are shown in equation (10):

where μ is a step size; N is a window size; and e^k is a prediction error from equation (9). Equation (10) shows how to obtain desired resulting images by repeatedly calculating and updating weights as in equation (11) with errors between the desired results and predicted results.

where g(x,y) is an input image; f(x,y) is a predicted image; w_k is a weight matrix repeated k times; and N is a window size.

Difference images, which highlight the background images estimated with a background estimation filter from the original images, have a relatively very bright value, which becomes a candidate target area. Background estimation results are compared and analyzed by obtaining the means of the target areas of difference images and those of the remaining areas and comparing their performance. The filter with the highest performance is used to detect a target candidate for multiple target tracking.

Multiple target tracking consists of a Kalman filter section (target position prediction) and candidate target classification section (target selection) in a system flow chart. The system removes error detection from the detection results of candidate targets in still images and associates targets in serial images. Target association refers to making a judgment to see whether a random target i detected in Image k corresponds with a random target detected in Image k+1. The Kalman filter used in the process can produce an error when the target path of the first order Kalman filter is nonlinear. However, the movement scope of each target is very narrow per image in the case of small infrared targets. The targets can thus be modeled linearly. Errors can also be adjusted using the accuracy enhancement technique for target tracking in the entire system.

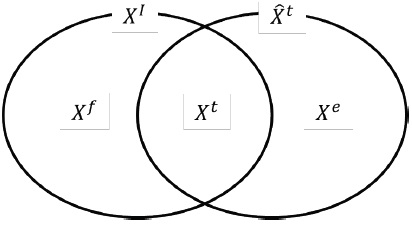
At the stage of detecting the locations of candidate targets in still images, targets are separated from backgrounds with the critical values of the original images and the difference images from the images obtained through a background estimation filter to acquire target locations. At the stage of classifying target candidates according to noises or targets, we calculate the candidate target location

predicted in Frame k with the path of the candidate target location (X^t_k？1) tracked in Frame k-1 by using a Kalman filter. In such a case, parameters such as a Kalman coefficient are updated and preserved with a target index. For classification, the candidate targets are classified into "candidate targets first detected (X ^f)" and "candidate targets that have been tracked (X ^f)" with the locations (X ^I) of targets detected in still images and the predicted locations

of targets that have been tracked. When the location information of targets detected in still images matches the predicted location information of targets that have been tracked, they are classified as "candidate targets that have been tracked (X ^f)." When there is no match between them, they are classified as "candidate targets first detected (X ^f)." The remaining are classified as "candidate targets detected with an error (X ^e)." These categories are shown in equation (12) and Fig. 2 below:

When candidate targets are classified as "candidate targets that have been tracked X ^f " according to the classification method, the reliability (C₁) of candidate targets being judged to be targets increases. When they are classified as "candidate targets detected with an error(X ^e)", the reliability (C₁) decreases.

The accuracy of target tracking can be enhanced by local histogram production, target model update, NCC model matching, and mean shift adjustment in a system flow chart. The system fine-tunes the locations of targets detected in still images and the locations of targets predicted with a Kalman filter, thus improving the stability of a target tracking system.

The stage of the fine-tuning target locations uses input images(F_k) and target locations(X^I_k) and produces local histogram models according to equation (13) below. The number of probing histogram models produced is determined by target locations(X^I_k) and M×M the certain area size in the surroundings.

where, N is the size of a local area needed to produce a histogram model; S(X) is the brightness value at Location X; and l is a histogram level and becomes L at 1 that is the scope of brightness value. NCC (normalized cross-correlation) is used to estimate the similarity between the produced histogram model and the standard histogram model produced at k-1. In such a case, NCC uses the following equation (14):

where H is a probing histogram, and T is a standard histogram. Since targets are associated with each other, a target location (X^I_k) corresponds to a standard histogram. The number of calculated NCC coefficients is determined using M×M, the number of probing histograms. A produced NCC map is used as a weight for the mean shift algorithm. On an NCC map, the mean shift vector of the mean shift algorithm is calculated in the direction of high NCC. In such a case, the maximum local value of an NCC map is obtained by carrying out a mean shift repeatedly until the mean shift vector becomes 0. The mean shift vector is shown in equation (15) below:

where g( ) is the derivative function of a Kernal function. Each target produces the local extreme value of NCC found with the mean shift algorithm. As it approaches increasingly closer to 1, the reliability of being judged to be targets (C₂) increases. The location of extreme values becomes X_k, which is the result of the entire system. Of the M×M histograms H(X^I_k) that correspond to each target X^I_k in the last stage of Hour k, the histogram that falls

into the location of the result (X_k) is updated as a standard histogram model.

An experiment was conducted to compare the performance of background estimation filters needed in the entire system.

The performance of background estimation filters is determined by comparing the difference operation means of the target areas and those of the remaining areas in the difference operation results of the background and original images calculated with each background estimation filter. Figure 3 shows images included in the target and background.

When the difference means of the target areas are high in the result images of the difference operation and have a greater difference from those of the background areas, the performance of the background estimation filter is considered to be excellent. Since the remaining areas other than the target areas can be seen as noises in the difference operation results, the ratio between target and background in Table 1 can be the signal-to-noise ratio (SNR). The experiment results reveal that the mean shift filter (MSF) had the highest SNR and was thus considered to be superior. It was used as a target candidate detection filter in a frame in the object tracking process.

The tracking performance of the proposed tracking system was examined by implementing and comparing the first order Kalman filter and the mean shift algorithm only. Thirty marine infrared serial images were used in the comparison, with four small targets that had a still image for one second. The proposed system was capable of processing when a new target was produced and lost, but the other systems in the comparison equation were not capable of such processing and accordingly used serial images with no target disappearance and production. The proposed system used a mean shift filter that demonstrated relatively good performance in the experiment for background estimation.

Judging the error detection of candidate targets or the assessment

of target reliability (C₁, C₂) was straightforward as follows: those candidate targets that were classified as "candidate targets that have been tracked (X ^f)" two or more times were classified as targets. Those candidate targets that were classified as "candidate targets detected with an error (X ^e)" of two or more were classified as error detection. Reliability C₂ was not used here.

Figure 4 shows part of the result image of introducing an experiment image into each tracking system. Figure 5 presents the mean location errors of four targets tracked with each tracking system. The first order Kalman filter had no diffusion in tracking locations and accordingly demonstrated relatively high stability, but its tracking location errors were high. The mean shift algorithm showed overall high tracking location errors as the target tracking location diffused and converged to a point in the sky starting with the 19th image. The proposed system recorded the lowest tracking location error except for the 18th image and showed relatively high stability with no tracking location diffusion.

The paper proposed a system to track the locations of multiple small targets in serial infrared images by using a background estimation filter, Kalman filter, and mean shift algorithm. The study compared and assessed various background estimation filters for performance and used a Kalman filter and candidate target classification to allow for target tracking and ensure no location tracking diffusion even in the case of target disappearance and production. In addition, the final target detection locations were revised with the mean shift algorithm having comparatively low tracking location errors and allow for continuous tracking with standard model updating. The experiment used each background estimation filter with actual marine infrared still images, obtained SNR in the original and difference images, and found that the mean shift filter recorded the highest SNR and relatively good performance. In the experiment with actual marine infrared serial images, the proposed system was compared with the Kalman filter and mean shift algorithm. As a result, the proposed system recorded the lowest tracking location errors relatively and ensured stable tracking with no tracking location diffusion.