본 연구에서는 리튬이온전지의 방전특성에 따른 열발생 속도를 계산하여 전지의 특성을 평가하였다. 이를 위하여 Butler- Volmer 식을 지배방정식으로 하여, 유사 2차원 모델링을 적용하고, 편미분 연산자인 FEMLAB을 이용하여 전산모사를 수행 하였다. 전류밀도를 5 A/m2에서 25 A/m2까지 증가시켜 계산을 수행한 결과, 전류밀도가 증가함에 따라 전극표면에서 고체 상 리튬의 소모량이 증가되는 것으로 나타났다. 이로 인한 확산제한의 발생시점이 단축되었으며, 동시에 리튬이온전지의 내부 전위가 컷오프 전위에 도달하는 시점에서 열발생 속도가 급격하게 증가되는 현상을 보여주었다.
리튬이온전지는 다른 전지보다 단위 질량, 부피당 갖는 에너지 밀도가 높고 사용목적에 따라 가볍고 작게 만들 수 있기 때문에 소형기기에서 상용화가 되어 있고, 리튬이온전지 특유의 높은 에너지 밀도 자체를 이용해 에너지저장 시스템과 같은 고용량 기기에 적용 가능한 신 에너지원으로 각광받고 있 다[1]. 다양한 다른 에너지원과 마찬가지로 리튬이온전지가 에너지원으로 존재하기 위해서, 비용 절감과 함께 지속가능한 에너지 공급기술이 지속적으로 발전해야 하지만, 리튬이온전지 개발 과정에서 생기는 화재 및 폭발에 대한 위험성은 전지의 안전성 확보 및 전지 내부 성능을 최적화를 하는데 있어 장애 요소가 된다[2]. 따라서 리튬이온전지를 수학적으로 전지 내부 특성이 충방전의 특성변화와 같은 여러 물리적인 변수를 이론적으로 모델링하는 것은, 리튬이온전지의 설계 및 최적화 연구에 있어 좋은 기반이 될 수 있다[3].
리튬이온전지가 여러 분야에서 쓰이고 있는 만큼 다양한 방전속도에 따라 전지의 특성을 평가하는 것은 매우 중요하다고 볼 수 있다. 특히 높은 방전속도 또는 전류 밀도에서는 전지 내부에서 여러 물리적인 요소가 급격히 변화하여 양 극간 고체상 또는 액체상에서 확산 제한이 일어날 수 있다. 확산 제한은 전지의 성능에 직접적으로 영향을 미치기 때문에 확산 제한이 일어나는 부분을 정확하게 찾을 필요가 있다. 또한 전지 특성 평가는 단순히 확산 제한뿐만 아니라 이상과열(thermal runaway) 등 전지 내부에서 일어날 수 있는 불안정성을 예측하는 것도 필요하다. 위 사항들을 수학적으로 접근할 때 전지 시스템의 이론적인 이해를 돕는 것과 동시에 빠르게 문제를 파악할 수 있어 전지 개발 향상에 대한 시간과 비용을 절약할 수 있다. 따라서 컴퓨터를 이용한 방전속도에 따른 리튬이온전지의 수학적인 모델링은 상대적으로 높은 방전속도를 요구하는 하이브리드 전기 자동차(hybrid electric vehicle, HEV)와 같이 고용량 기기에 적용하는데 있어 효과적인 방법이라 할 수 있다.
전지 특성을 평가하는 가장 일반적인 방법은 전류-전위 그래프를 이용하여 활성화도(activation), 저항성(resistibility), 농도 과전압(concentration overpotential)을 평가하는 것이다. 위과전압(overpotential)은 전지 내부의 온도, 충방전 속도 기타 여러 가지 전지 상태에 따라 크게 영향을 미친다. 특히 농도 과전압의 경우 전지의 수명이 다하는데 영향을 끼치므로 이 부분에서 전지의 방전용량이 결정될 수 있다[4]. 수학적인 모델링을 이용하는 경우 전류-전위 곡선을 비교적 빠르고 쉽게 만들 수 있기 때문에 확산제한을 효율적으로 평가할 수 있다.
본 연구에서는 리튬이온전지를 유사 2차원 모델링으로 단순화하여 방전속도에 따른 전지 내부의 특성을 평가하였다. 각 변수들의 특성을 평가하기 위하여 등온상태 모델링을 수행 하였으며, 방전속도는 방전 전류밀도를 경계조건으로 설정하였고 확산제한이 걸리는 시점을 기준으로 전지의 특성을 평가하였다. 또한, 등온 모델링을 통하여 각 전류밀도에 따른 열발생 속도(heat generation rate)을 평가하여 전지 내부에서 방출하는 열발생 속도를 정량적으로 예측하고자 한다.
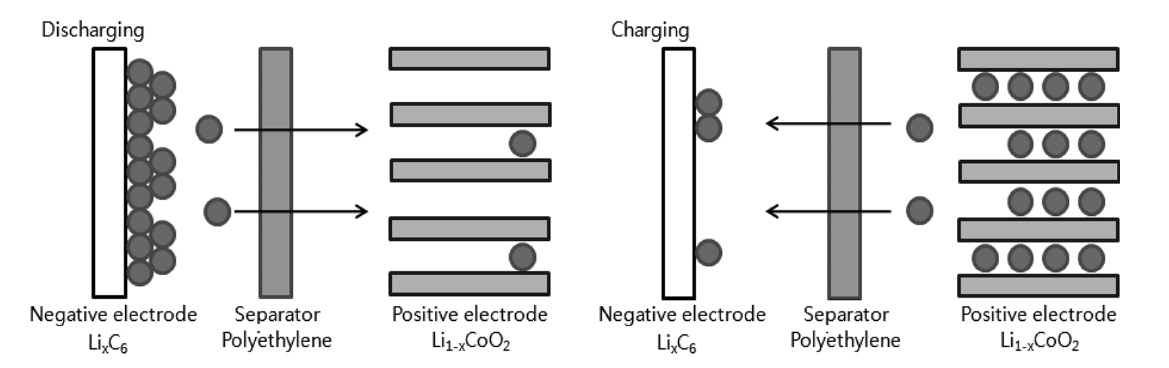
본 연구의 계를 Figure 1에 도시하였다. Figure 1에서 리튬 이온 셀은 음극과 양극 그리고 두 극 사이로 분리막이 존재한다. 전극 표면에서 전해질과 함께 전극 반응이 일어나고 전극 반응 물질인 리튬이 전극에서는 고체상으로 전해질에서는 액체상으로 존재하기 때문에 수학적으로 표현할 경우 전하방정식과 물질전달 방정식을 액체상과 고체상으로 각각 2개를 적용한다. 리튬이온전지의 변수들은 Kumaresan et al.[5]와 Valoen and Reimers[6]의 연구 결과를 이용하였으며 해당 변수들의 목
[Table 1.] Design parameters of the present lithium-ion cell[5]
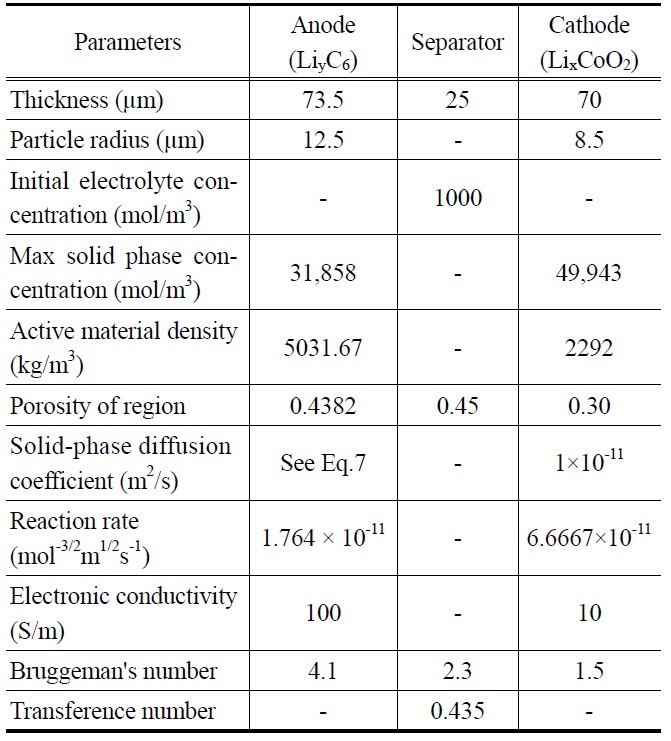
Design parameters of the present lithium-ion cell[5]
록은 Table 1과 같다. 본 연구에서 적용하는 리튬 이온 셀을 음극물질은 메조 카본 마이크로 비드(meso carbon micro bead, MCMB), 그리고 양극 물질을 LiCoO2로 적용하였다.
옴의 법칙에 따라 고체상에서 전하 이동에 의해 발생되는 전위의 분포는 다음의 식과 같다.
여기서
[Table 2.] Boundary conditions for FEMLAB modeling[5]

Boundary conditions for FEMLAB modeling[5]
여기서 ?는 액체상에서의 전도도를,
여기서
또한, 고체상에서의 물질 전달은 전극이 구형형태의 입자형태로 이루어져 있다는 것으로 가정하여 Fick's law에 의해 다음식으로 결정된다[7].
고체상에서의 확산계수
식 (5)의 경우 다른 지배방정식과 달리 구형좌표계를 가지고 있기 때문에, 본 연구에서는 극 중심부에서 표면까지를 2차원의 형태로 바꾸어서 적용하였고, 기존의 1차원 지배방정식과 연결하기 위해 Butler-Volmer 방정식을 이용하였다. 전자 전달이 전극과 전해질 모두 표면에서 발생한다고 가정 하였을 때, Butler-Volmer 방정식은 다음 식과 같다.
식 (6)에서 ?는 표면 전기화학의 반응상수이고,
다른 1차원 지배방정식의 경계조건은 Kumaresan et al.[5]의 연구의 결과를 이용하였으며, 이를 정리하면 Table 2와 같다.
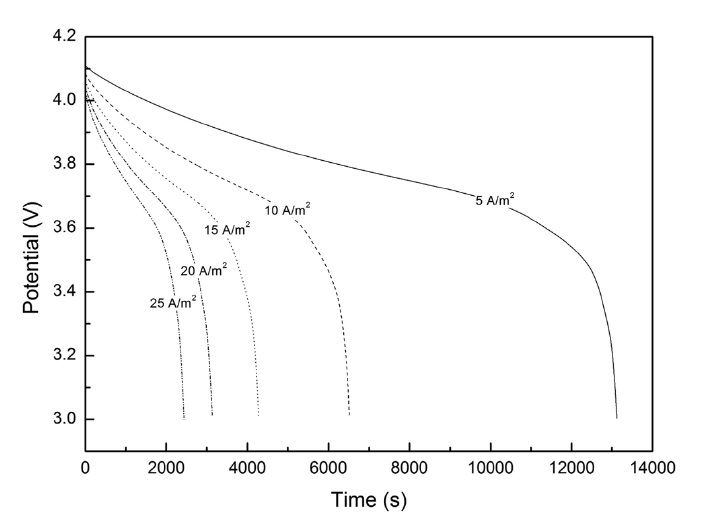
방전속도에 따른 리튬 이온전지의 방전 특성을 알아보기 위해 전류밀도를 5 A/m2에서 25 A/m2까지 설정하였고 컷오프 전위가 3.0 V일 때 확산제한이 일어나는 시점을 계산하였다. 계산결과를 Figure 2에 나타내었다. Figure 2에서 보면, 5 A/m2에서는 13120초, 10 A/m2는 6516초, 15 A/m2는 4280초, 20 A/m2는 3136초, 그리고 25 A/m2에서는 2436초이며, 5 A/m2의 낮은 전류밀도보다 25 A/m2의 높은 전류밀도에서 약 0.18배 정도로 확산제한이 빨리 일어났다. 확산제한 뿐만 아니라
높은 전류밀도에서 전기저항(ohmic resistance) 역시 급격하게 증가하는 것을 알 수 있었다. 즉, Figure 1의 상황에서 전극표면에서의 반응속도가 확산속도보다 빠르다는 것과 동시에 리튬 또는 리튬이온이 양극 사이로 움직일 때 생기는 저항 역시 같이 커진다는 것을 의미한다. 이런 경우 Doyle et al.[3]의 결과에서는 높은 전류 밀도에서 농도제한보다는 전기저항(ohmic resistance)이 더욱 지배적으로 영향을 받는다고 했으나, Doyle et al.의 I-V그래프에서 높은 전류밀도에서의 전위차가 급격하게 떨어지는 부분이 없는 것을 확산제한이 일어나지 않는 것이라고 볼 때, 본 연구에서는 전기저항보다 전극 표면의 확산 제한이 지배적이라고 볼 수 있다.
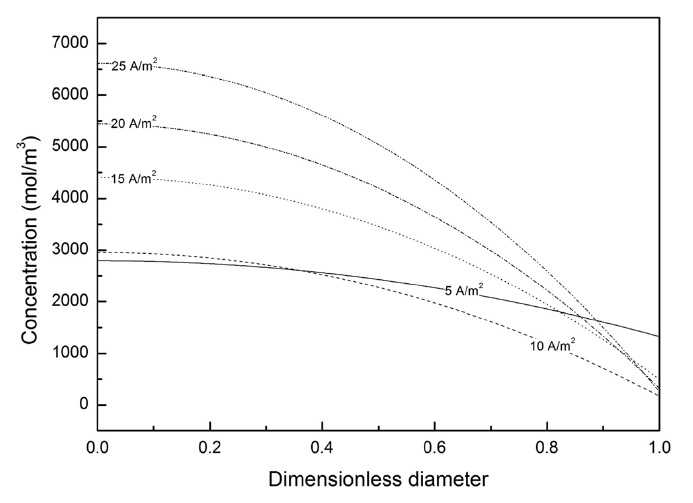
Lee and Yoon[9]의 최근 연구에서도 언급 했듯이, 확산제한이 빠르게 일어날수록 전극 표면에서의 반응속도보다, 고체상 리튬의 확산속도가 더 느리다는 것을 보여준다. 따라서 상대적으로 느린 확산속도에 의해 전극 표면에서의 농도와 중심부의 농도 구배가 커짐을 알 수 있다. 이러한 현상은 Figure 3과 같이 음극 중심부에서 표면까지의 농도 구배로 설명할 수 있다. Figure 3에서 보면 컷오프 전위(cut-off voltage)에 도달 했을 때 전극 중심부에서 표면까지의 농도구배는 5 A/m2에서 14066.94 mol/m3, 10 A/m2에서 2781.91 mol/m3, 15 A/m2에서 3911.45 mol/m3, 20 A/m2에서 5120.33 mol/m3, 그리고 25 A/m2에서 6358.59 mol/m3으로 방전속도가 빨라질수록 농도구배가 커지는 것을 확인할 수 있다. 또한 10 A/m2 이상의 전류밀도에서 전극 표면에서의 고체상 리튬 농도가 0에 근접하는 것으로 볼 때 액체상이 아닌 고체상에서 확산제한이 먼저 일어나는 것을 알 수 있다. Figure 2와 3에서와 같이 전극 표면에서 확산제한이 일어난 것을 알 수 있으나 고체상 리튬의 확산 계수와 전기화학 반응상수가 상수로 고정되어 있기 때문에 이 경우 전류밀도에 따른 물질소모 양이 그 원인인 것으로 고려된다.
와 25 A/m2에서 모두 방전 초기에는 서로 농도차이를 보이지 않다가 시간이 지나면서 급격하게 차이 나는 것을 볼 수 있다. 5 A/m2에서는 1000초일 때 표면에서의 농도가 20067.95 mol/m3, 2000초일 때는 18285.35 mol/m3인 반면 25 A/m2에서 표면에서는 1000초일 때 9018.09 mol/m3 그리고 2000초일 때 3119.55 mol/m3으로 높은 방전 전류밀도에서 소모되는 리튬의 양이 많다는 것을 알 수 있다. 뿐만 아니라 전극 표면에서 소모되는 고체상 리튬의 양이 달라지면 식 (7)에 의해 전극 표면에 서 일어나는 전기화학 반응 역시 방전속도에 따라 변화하게 된다. 따라서 고체상에서 같은 확산계수로 물질이 이동할 경우 방전 전류밀도에 따라 소모되는 고체상 리튬에 따라 확산제한이 좀 더 빨리 일어나는 것을 알 수 있다.
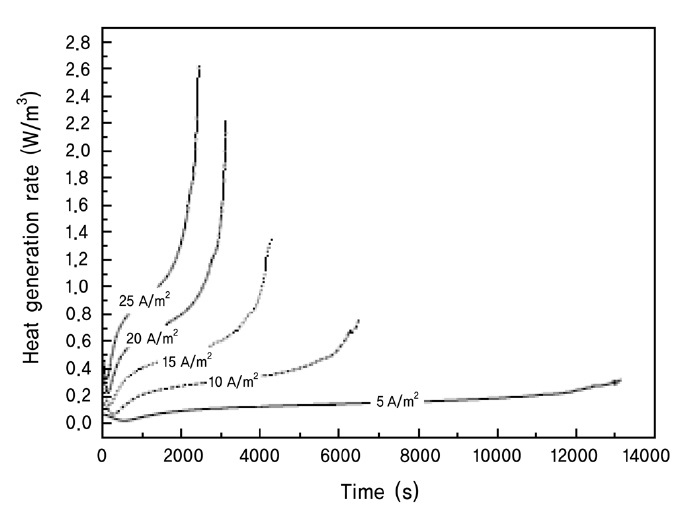
등온 모사에서 열발생(heat generation)은 생성되는 즉시 시스템 밖으로 나간다고 가정하기 때문에, 실질적으로 변수에 영향을 미치지는 않지만 방전속도에 따라 어느 정도 열이 발생하는지에 대한 전지의 불안정성에 대해 간접적으로 평가할 수 있다. 본 연구에서는 다음과 같이 열발생 속도(heat generation rate)를 평가하는 식을 도입하였다 Figure 4. Concentration profiles of negative electrode evolving with time. [8].
위 식은 전극표면과 전해질에서의 전자전달 과정에서 생성되는 열발생 속도(heat generation rate)
와 가역적인 부분인
본 연구에서는 유사 2차원 상태 모델링을 이용하여 방전속도에 따른 리튬이온전지의 방전특성을 모사하였다. 그 결과 방전속도가 빠를수록 확산제한이 걸리는 시간이 빨라졌으며 확산제한이 일어나는 원인이 전극표면에서 전기화학반응에 의해 소모되는 고체상 리튬의 양이 방전속도가 증가할수록 많아지기 때문이라는 것을 계산을 통하여 확인하였다. 또한 등온모델링을 통하여 전기화학 표면에서의 열발생 속도를 적절한 상태방정식을 이용하여 계산한 결과 높은 방전속도에서 열 생성속도가 빠르게 일어났으며, 변화율이 크게 일어난 시점이 확산제한이 일어난 시점으로 볼 때, 확산제한이 열을 발생시키는데 원인이 될 수 있음을 확인할 수 있었다.
![Design parameters of the present lithium-ion cell[5]](http://oak.go.kr/repository/journal/11672/CJGSB2_2012_v18n3_320_t001.jpg)
![Boundary conditions for FEMLAB modeling[5]](http://oak.go.kr/repository/journal/11672/CJGSB2_2012_v18n3_320_t002.jpg)