With the advent of ubiquitous computing devices equipped with global positioning system (GPS), radio frequency identifi-cation (RFID) or sensors, we can easily record object move-ments or trajectories. Recently, much research work [1-4] has aimed to evaluate spatio-temporal queries, such as range and nearest neighbor queries, on a trajectory database from the given query point.

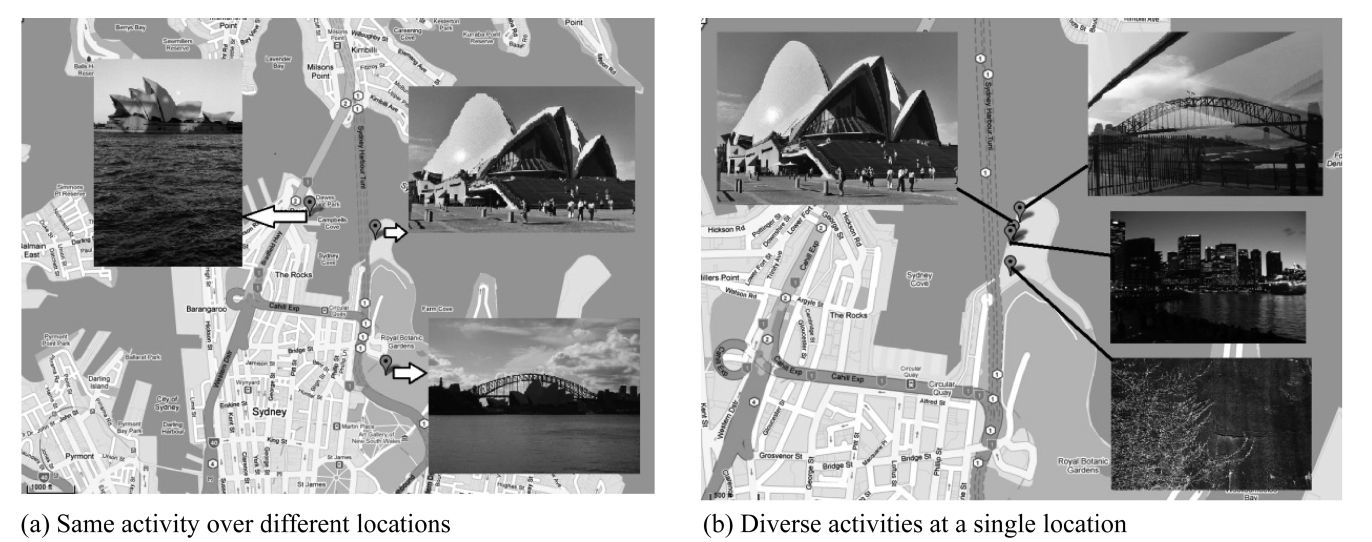
While most existing work focuses on supporting trajectories that record only the locations over time, the actual trajectories collected from recent location-based services often have greater semantic richness. For example, Flickr (flickr.com) allows users to geo-tag their photos and annotate them with comments and tags. This enables users to describe their trips as a trajectory of photos and information, for example, Fig. 1 shows a geo-tagged photo of the opera house on the map with annotated information such as title, username or timestamp. Such additional informa-tion enables us to bridge the semantic gap between the location and the actual activity at the location, by distinguishing between different activities that occurred at the same location, or the same activities at different locations, as Fig. 2 illustrates. Recent work [5], distinguishing activities from locations using user comments, has the same goal as ours: supporting semantic-rich location-based service.

The scale of such semantic-rich trajectories, e.g., millions of geo-tagged images added monthly to Flickr, naturally motivates us to support advanced data analysis (e.g., clustering), e.g., rec-ommending interesting travel itineraries [6].

Our goal is to enable online clustering of semantic-rich tra-jectories, motivated by the following example scenario.

Example 1. While existing forms of travel recommendation, e.g., travel guides or portals, focus on offline computation ren-dering the same itinerary for all users, travel recommendation on ubiquitous devices naturally motivate forms of online rec-ommendation that can adapt to changes in user-specific context. For instance, the recommendation should vary according to the temporal context, such as time of the day or season of the year.

We thus propose to study online trajectory clustering algo-rithms, combining the following semantic context criteria:

Soft criteria: Users may embed various semantic informa-tion, e.g., semantic geographic information, in the similar-ity measure.

Hard criteria: Users may consider only trajectories satisfy-ing some Boolean semantic criteria, such as time = evening or user = Tom.

In this paper, we focus on combining the two semantic con-text criteria with clustering, which can be easily provided by the user at the query time. However, existing clustering algorithms cannot address this problem due to the following challenges. First, most existing work focuses on offline unconstrained loca-tion trajectories, such as hurricanes or animal trajectories. In contrast, in many location-based services, trajectory mining should reflect the proximity with respect to the underlying con-straint, e.g., road networks or subway routes, because two nearby locations can be very hard to reach if no roads connect the two locations. We study online clustering, which supports soft semantic criteria using a similarity measure based on the underlying geographic information such as road networks.

Secondly, to support hard semantic criteria, we need to sup-port Boolean + Clustering queries efficiently. While existing clustering algorithms can be adopted after Boolean conditions are evaluated, such naive adoption incurs a significantly high computational cost, which provides motivation for an integrated algorithm capable of evaluating both.

To this end, we design a summarized data structure where pre-computed initial clusters of trajectories are stored. This can expedite online computation in order to merge these initial clus-ters. We store statistical information on selection attributes to reflect Boolean selections in the merging process.

This paper addresses the above challenges, which is an extension of our preliminary work [7] that only tackled the first challenge. We discuss our extension of this preliminary work in Section II. The main contributions of this paper are as follows:

We are motivated to study the problem of supporting Bool-ean + Clustering queries for semantic-rich trajectories.

We design a summarized structure for pre-materializing ini-tial trajectory clusters.

We propose an efficient clustering algorithm built on the proposed summarized structure.

We extensively validate the effectiveness and the efficiency of our proposed framework using real-life trajectory data.

The rest of the paper is organized as follows. Section II pre-sents the prior research work. In Section III, we present the for-mal definition of our problem. Section IV studies distance measures. Section V describes our clustering algorithms. Sec-tion VI reports our experimental results. Section VII concludes this paper.

Lately, clustering trajectories have been studied actively, but most work assumes trajectories without road network con-straints, as in hurricane tracking or animal movement data. For trajectories without constraints, trajectories are typically repre-sented by either a set or sequence of locations (sampling points), for which similarity metrics have been proposed in [8-13] and [14-17], respectively.

In a clear contrast, this work focuses on trajectories that are constrained by road networks, for which a similarity metric has only recently been proposed in [7]. In many real-life applica-tions, moving objects are often constrained by obstacles such as buildings, trees, or roads. Roh and Hwang [7] studied a similar-ity metric that reflects such constraints in trajectory analysis.

Once similarity metrics are defined, existing clustering algo-rithms can be applied to group trajectories into clusters. Specifi-cally, recent work [18] proposes to adopt the expectation maximization (EM) algorithm and density-based clustering algorithm [12] for the task of clustering trajectories. However, these algorithms are not suitable for our proposed problem of online clustering with Boolean selection conditions. Gaffney and Smyth [18] requires slow convergence, which prohibits online responses, while [12] requires to pre-materialize an index struc-ture for online computation, which will be ineffective when there exist Boolean selection conditions.

Our preliminary work [7] distinguishes itself from the exist-ing work by designing a distance function for network-con-strained location trajectories and developing an online algorithm. Based on this preliminary work, we extend our algo-rithms to support semantic-rich trajectories, archiving not only location changes, but also semantic information such as images, text, user ID and tags.

In particular, our study aims to support Boolean selection of semantic features in this paper. For efficient support, we pro-pose to minimize online computational requirements, as simi-larly adopted for numerical data in [19]. However, adopting [19] for our proposed problem is not desirable, as this work assumes two objects with similar selection attribute values are also deemed to be similar according to the similarity metric. This assumption does not hold in our problem, where similarity and selection attributes are allowed to be independent, e.g., sim-ilarity of image features and selection of timestamps.

The most relevant work [5] to this paper distinguishes activi-ties from locations using comments added by users on the tra-jectory. This work has the same goals as ours; we support Boolean conditions or texts or tags, such as tag = dining. A key distinction of our work from the existing work is to provide a systematic framework for online clustering with arbitrary Bool-ean semantic conditions.

In this section, we formally define our problem. We begin by modeling a network-constrained trajectory. We model a road network as a graph, where an edge is a road segment and a ver-tex is an intersection of adjacent segments, formally stated as follows:

Definition 3.1 Road network. A road network (RN) is defined as a graph G_RN = (V, E), where V is a set of intersections of the road network, and E is a set of road segments R_i ∈ E such that

Ri = (ri,s, ri,e),

where r_i,s, r_i,e ∈ V and there exists a road between r_i,s and r_i,e.

The trajectories on the road network can thus be represented by a set of connected road segments, or edges in the above-mentioned graph. Methods of matching GPS logs to road seg-ments have been studied in existing map matching literatures (e.g., [20]).

Definition 3.2 Network-constrained trajectory. Given a road network G_RN = (V, E), a trajectory of length l is defined as

TRi = [ti1 , ..., til],

where tⁱ_j∈ E, 1 ≤ j ≤ l and tⁱ_j and tⁱ_j+1 are connected.

We formally define our problem of finding a set of disjoint clusters C for trajectories that satisfy the given Boolean condi-tion set B. The Boolean condition set can be a complex Boolean condition such as conjunctions and disjunctions of sub-conditions.

Definition 3.3 Problem statement. Given input trajectories T that satisfy Boolean selection condition set B, our goal is to find C = {c_q, ..., c_|C|}, maximizing the sumof inter-cluster distances, such that

where the inter-cluster distance D_inter is defined by the distance between representative trajectories of two clusters. Note that our target problem does not require users to specify a fixed number of clusters.

Definition 3.4 Inter-cluster distance. Given two clusters, c i and c j, the distance between them is defined by

where rt(c_i) is the representative trajectory of a cluster c_i , i.e.,

and D(·,·) is the trajectory distance, which we will define in the next section.

In this section, we discuss a distance measure between net-work-constrained trajectories. To define a desirable distance measure, we have to consider the following two requirements:

Accuracy: The distance measure should accurately reflect the spatial proximity from the viewpoint of the road network.

Efficiency: The distance measure should be a metric for effi-cient computation of clustering, as we will elaborate in the details in Section V.

While distance measures satisfying the above requirements for trajectories without road network constraints have been actively studied [12-15], the distance measure for network-con-strained trajectories has only recently been proposed in our pre-liminary work.

To address the first requirement that spatial proximity must be accurately represented, our distance measure adopts the intu-itive notion of the Hausdorff distance to quantify the distance of two trajectories TR_i and TR_j as the longest road network path from each road segment to its closest road segment in the other trajectory. More formally,

Definition 4.1 Trajectory distance [7]. Given two trajectories TR_i = [tⁱ₁ , ...,tⁱ_n] and TR_j = [t^j₁ , ..., t^j_m], the distance between them is defined as follows:

where

(TR_i, TR_j) is the one-way trajectory distance from TR_i to TR_j, defined as:

Meanwhile, the road segment distance d (·,·) in the previous definition is defined as follows:

Definition 4.2 Road segment distance [7].

where

(R_i, R_j) is a one-way road segment distance from R_i to R_j defined as:

where |a,b？ is the length of the shortest path between a and b.

To address the second requirement of efficient computation, we show that our distance measure is a metric.

Theorem 4.3. Trajectory distance in Definition 4.1 is a metric.

Proof. Given three trajectories TR_i, TR_j, and TR_k, Equation 3 and 4 satisfy the following properties.

The symmetric property follows from 3, the reflexive prop-erty follows from 1 and 2, and the triangle in equality follows from 4.

As the symmetric and reflexive properties are obvious from the definition, we only present the proof of triangle in equality. First we consider ε-neighborhood road segments of a trajectory, denoted by N_ε(TR), which are road segments within εdistance from any road segment in TR.

With this notion, the proof of triangle inequality is as fol-lows. For convenience, we shortly denote

(TR_i, TR_j) by

Similarly,

From Equation 7 and 8, the following inequality holds.

In this section, we present a clustering algorithm called Sem-Cluster, which supports Boolean + Clustering queries for seman-tic-rich network trajectories. As NNCluster [7] is an online algorithm, it can be naively adopted for Boolean + Clustering queries, by evaluating Boolean selection first and performing NNCluster only on the qualifying results. However, such naive adoption incurs a high cost, especially when the selectivity of Boolean conditions is high.

To address this challenge, the basic concept of SemCluster involves minimizing the distance computations at runtime by pre-materializing initial clusters into a summarized data structure. Based on this concept, we devise SemCluster with two key com-ponents？BuildDS and MergeDS. The BuildDS module material-izes the summarized data structure from trajectories in an offline process. The MergeDS module performs Boolean + Clustering queries with the pre-materialized summarized data structure.

As we exploit the same property, sharing common nearest neighbors, of NNCluster when we identify initial clusters, we first give a brief review on identifying initial clusters in Section V-A. We then present the BuildDS module in Section V-B and the MergeDS module in Section V-C.

We briefly review our method of identifying initial clusters of trajectories. We group the trajectories into initial clusters that are likely to belong to the same cluster. To decide which trajec-tories to put into the same initial cluster, we need to identify a set of trajectories sharing the common nearest neighbor. This problem can be abstracted as a graph problem, by denoting each trajectory as a node connected to another node that is the nearest neighbor. Given this graph, the problem of building the initial clusters can be reduced to listing all maximal cliques, which is known as an NP-complete problem [21].

Our goal is to approximate this process by relaxing the notion of initial clusters to those sharing many k-nearest neigh-bors. To effectively construct initial clusters, we compare the k-nearest neighbors of each trajectory with those of another tra-jectory. The two trajectories are then merged into a cluster if the ratio between the common nearest neighbors is greater than a user-defined threshold value. Interested readers may find the details on identifying initial clusters and setting the threshold value in [7].

This section describes our method of pre-materializing a summarized data structure from the trajectories in the database. The summarized data structure consists of two components: 1) initial cluster information and 2) the distance relationship between initial clusters.

Once initial clusters are identified, we store the information of the initial clusters, such as the representative trajectory of the initial cluster and the number of members. We compute the rep-resentative trajectory of each initial cluster using Equation 2. We choose a hash table to store the information of the initial clusters for fast retrieval. More specifically, for each member of an initial cluster, the key-value pair of (tid, (refid, s)) is inserted into a hash table, where tid is an identifier of a trajectory, refid is an identifier of a representative trajectory, and s is the number of trajectories that belong to the initial cluster represented by refid. For example, for the initial clusterc₁ = {t₃ , t₅ , t₆ }, we store key-value pairs such as (3, (5, 3)), (5, (5, 3)), and (6, (5, 3)) in the hash table, when t₅ is the representative trajectory of c₁.

In addition, we also compute and store the distance relation-ship between all pairs of representative trajectories using Equa-tion 1, which will reduce the number of distance computations at runtime. If there are n initial clusters, we build an n × n dis-tance matrix DM, where DM_ij contains inter-cluster distances between c_i and c_j.

SemCluster invokes MergeDS when users issue Boolean + Clustering queries. This section presents the method by which MergeDS exploits the above pre-materialized summarized data structure to merge initial clusters into meaningful groups. MergeDS consists of two components: 1) finding initial clusters satisfying given Boolean conditions and 2) merging them and maximizing the sum of inter-cluster distances.

Given a Boolean + Clustering query, we first search the data-base for trajectories satisfying the Boolean conditions. Then, we look up the hash table of the summarized data structure to iden-tify the initial clusters of trajectories satisfying the Boolean con-ditions. Each identifier of a trajectory is used as a key. Using a hash table, we can effectively identify the initial clusters of tra-jectories that satisfy the Boolean conditions. Moreover, we can accelerate this step by linking leaf nodes of an index structure, which is built for a selection attribute, with the bins of the hash table.

For the initial clusters identified in the previous step, we find the disjoint clusters maximizing the inter-cluster distance D_inter, which is known to be NP-hard [22]. We develop a greedy approach, which continues merging a pair of clusters in ascend-ing order of inter-cluster distance until a stop condition is satis-fied. Note that the inter-cluster distance has been previously computed and stored in the distance matrix of the summarized data structure. Therefore, SemCluster does not require distance computations for all pairs of representatives but instead refers to the distance matrix for determining the order of merging clusters.

In each merging step, e.g., c_i and c_j, SemCluster elects a tra-jectory as a new representative trajectory of merged cluster c_i∪ c_j. Between two representatives of c_i and c_j, the representa-tive from the larger cluster is promoted to be a new representa-tive of c_i∪c_j. To this end, we store the number of member trajectories in each merging step.

As a stop condition, we use the DB index [23], which is a quality measure validating the clustering results. Given a set of clusters C = {c₁, ..., c_n}, the DB index is defined as:

where

d_ij is is the distance between cluster c_i and cluster c_j, and s_i is the variance of cluster c_i. The DB index approaches 0 as the clusters get more compact and well-sepa-rated. We note that the computation of the DB index does not require any additional distance computation between trajecto-ries, which incurs high costs. We store the value of the DB index at each merging step. Then, we report the clustering result that minimizes the DB index.

We report the experimental results conducted to verify the effectiveness and efficiency of SemCluster for semantic-rich trajectories.

For semantic-rich trajectories, we collected geo-tagged images from the Flickr website using Flickr API. There were 1, 505, 768 geo-tagged images, which were taken between 1st Jan-uary 2001 and 31st December 2009 in Australia. The collected images were first grouped according to their user ID, and then the images of each user were sorted in order of time taken. We then split the image sequence of each user into disjoint sub-sequences by discretizing the 24-hour period into 12 range groups. As a result, 314, 000 semantic-rich trajectories are stored in the database.

All experiments were conducted on a machine with a Pen-tium-4 (3.2 GHz) CPU and 1 GBytes of main memory, running a version of the Linux operating system. We implemented our proposed algorithms using the C programming language. All trajectories were stored in an Oracle Berkeley DB (Version 4.6). The B-tree index was built on the database for efficient retrieval of Boolean selections.

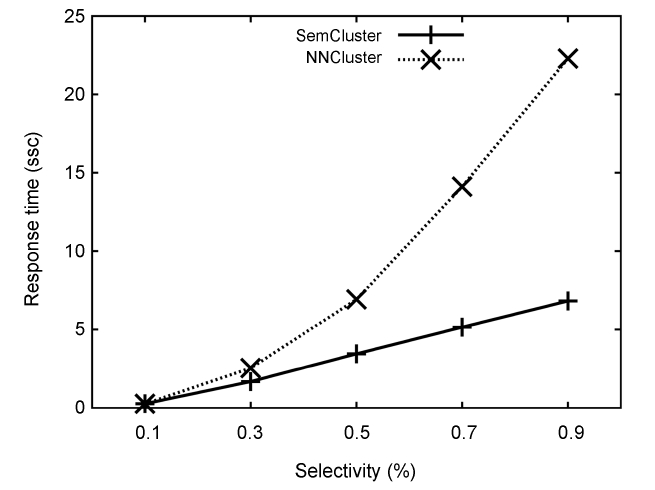
In this section, we validate the efficiency of SemCluster in comparison with NNCluster [7] using the response time as a metric, by varying the selectivity of the Boolean conditions. Note that in contrast to NNCluster, SemCluster does not require

any distance computations at runtime. Therefore, the perfor-mance gap between NNCluster and SemCluster will increase, if an expensive semantic-aware distance measure is used (e.g., computing the image similarity).

As shown in Fig. 3, SemCluster outperforms NNCluster in all experimental settings. The speedup of SemCluster increases as the selectivity grows. We achieve this speedup by pre-com-puting the trajectory distance computation when building the summarized data structure, and only handling references to inter-cluster distance in the distance matrix at runtime.

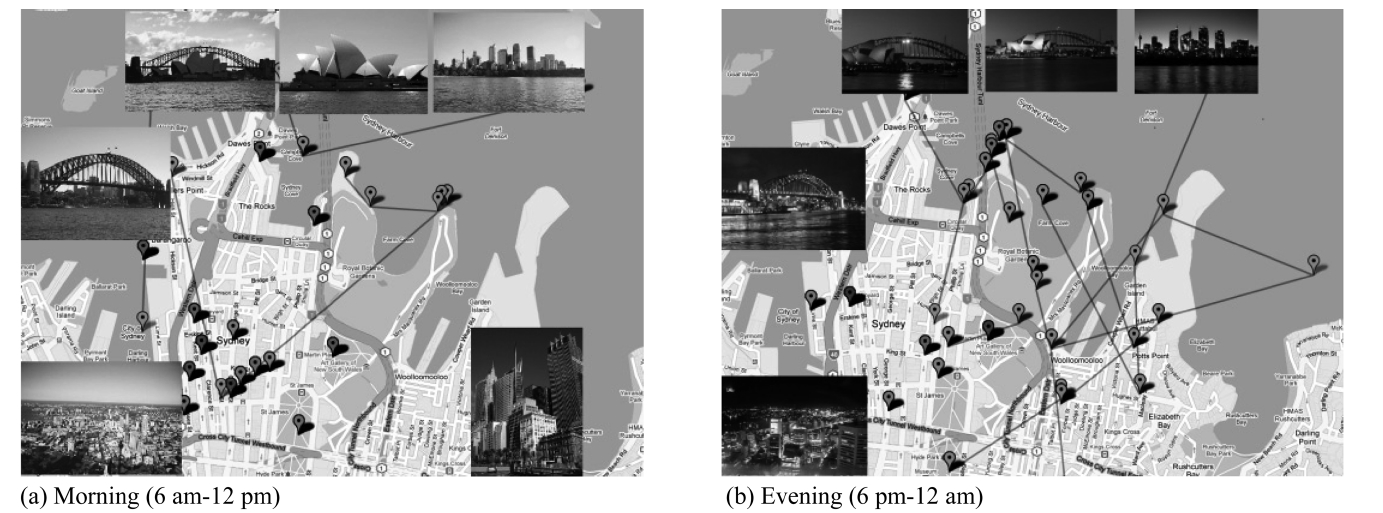
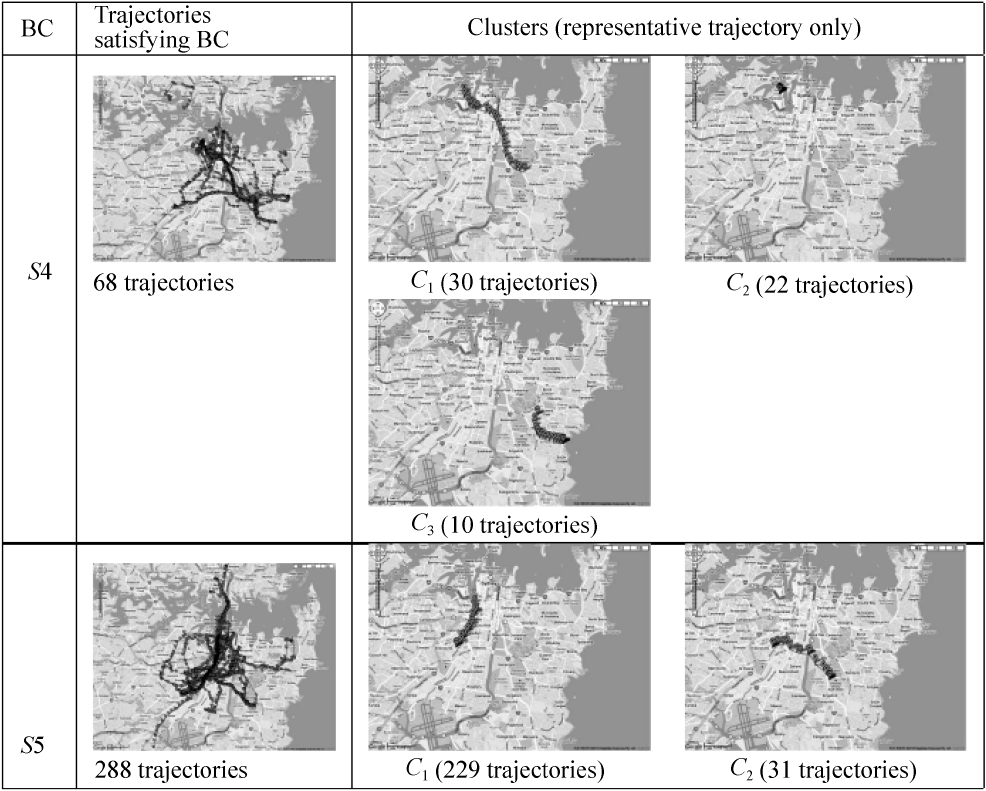
In this section, we validate the quality of the clustering results produced by SemCluster. More specifically, we visualize the clustering results for Boolean selections of timestamps or user ID.

A) Selection of Temporal Attributes: Scenarios for combining clustering with selection conditions of timestamps include find-ing clusters for different times of day or different seasons of the year. In this section, we demonstrate the clustering results for trajectories in the morning (S1), during lunchtime (S2) and in the evening (S3). Fig. 4a and 4b contrast results for S1 and S3？ Note the cluster identified for S3 (evening) shows night view spots near the coastline, while the results for S1 (morning) includes more locations in downtown.

B) Selection of User ID: Selection conditions can be added to user ID to identify user-specific trends. We observe user-spe-cific trends in the clustering result of semantic-rich trajectories. We use Flickr user ID as a selection attribute.

Fig. 5 illustrates trajectories satisfying the following Boolean condition:

S4. : user ID = 2905XXXX@N02

S5. : user ID = 2906XXXX@N04.

We also present the clustering result in Fig. 5 for each Bool-ean condition. For the purposes of presentation, we plot only the representative trajectory of clusters and we do not visualize small clusters with sizes less than 15% of the largest one. As

shown in Fig. 5, the clustering results for S4 and S5 show the user-specific trends in semantic-rich trajectories.

In this paper, we studied a method to integrate a Boolean selection with clustering for mining semantic-rich trajectories. Specifically, we designed a new framework pre-materializing a summarized data structure for the whole dataset, and proposed a greedy clustering algorithm building on this structure. We vali-dated the effectiveness and the efficiency of our results using real-life location trajectories and semantic-rich trajectories col-lected from the Flickr website. Our proposed framework enables us to capture temporal characteristics of clusters and outperforms the baseline algorithm proposed in our preliminary work. For future work, we are investigating the efficient main-tenance of the summarized data structure, in case of frequent updates in the trajectory database.