The goal of image registration is to find out the geo-metric transformation of two or more images of the same scene that are taken at different instances, from different sensors or from different viewpoints and align them into the same spatial coordinate. The alignment is done by taking one image as reference and the other one as a float (image to be registered) and then, transform the float image to the same spatial coordinate of the reference image. It is one of the essential processes for different application fields in image processing such as medical imaging or remote sensing [1]. Medical images that are obtained from different modalities have different charac-teristics and properties. Integration or subtraction of images that are obtained from different modalities or the same modality is often desired for the evaluation of surgical or clinical diagnostic setting and other treatment problems. This is a critical task for medical image applications, as a registration technique is needed to complete this task for consistent and repeatable analyses.

Many registration techniques have been developed for the various medical imaging problems. The development of effective registration techniques has been demanded for efficient clinical applications. Registration can be divided into rigid or non-rigid, according to the nature of the transformation [2]. Rigid registration is simpler, as its transformation in three dimensions is defined by six parameters: three for rotations and three for translations. Conversely, non-rigid registration is more complex. Besides, rotations and translations it involves voxel-dependent dis-tortion. Although rigid transformation is simple compared to non-rigid transformation, it is a crucial task for regis-tering rigid structures such as bones, and it is often per-formed as a preliminary step for some non-rigid registration [3, 4].

From the aspect of the type of features that are used in a registration, the existing automatic registration methods are further divided as feature-based or intensity-based methods. Feature-based methods extract the corresponding features or attributes between a reference and the float images for registration. Common features include points, edges, contours or surfaces. These features may be specified manually or extracted automatically. Among the feature-based rigid registration methods, the principal axis regis-tration (PAR) method [5] is the most motivating one as it can easily find the transformation parameters by calculat-ing the principal axis of a common feature that is extracted from a reference and the float images.

PAR registration consists of translating the centroid of a float onto the reference image, and then, rotating it about the centroid to align the 3D principal axes of both the images. Hence, good features need to be extracted to obtain the accurate principal axes and centroids. In most of the 3D cases, a binary structure image [6, 7] is used as features while the contour features [8] are extracted for 2D principal axis registration. The main advantages of the feature-based principal axis registration methods are simple, and they are less computationally complex. Despite good properties, these approaches have been less popular as they can lead to inaccuracies in a medical image registration.

Intensity-based methods that uses full image content is the most interesting work, as they provide more reliable results with higher accuracy and this makes thees meth-ods suitable for clinical application [9]. These approaches are commonly known as the voxel similarity based meth-ods for 3D cases. These methods solve the registration task as a mathematical optimization problem. They use a similarity measure as a cost function to gauge the quality of the alignment between the reference and the float images for any given transformation. Obviously, finding out the optimized parameters between the two images needs the maximization of the similarity or the minimiza-tion of the difference. Common similarity metrics are mutual information (MI), normalized mutual information (NMI), cross correlation (CC), normalized cross correlation (NCC), sum of squared differences (SSD) and sum of absolute differences (SAD) [10, 11]. MI or NMI is consid-ered as the most suitable metric for the multimodal image registration [12, 13] while the rest of them are appropri-ate for mono-modality image registration [14-16].

There are many mathematical optimizers that are sug-gested for image registration. Common optimizers include Powell’s, downhill simplex method, steepest descent, quasi-Newton, Levenberg-Marquardt, and conjugate-gra-dient method [17]. These approaches usually apply the voxel value of original intensity images and use an opti-mizer. Gradient NMIs based registration has been proposed for the registration of 3D CT data to 2D endoscopic image [18]. This approach calculates the NMIs in the gra-dient images as well as in the original intensity images and it adopted two optimizers, Powell’s and downhill simplex method. The voxel similarity method has been known to provide high accuracy for clinical application but due to their high computational cost, their usage in 3D clinical applications has been limited.

In order to diminish the computational complexity of the voxel similarity based methods, multi-resolution approach has been developed by using the hierarchical structure of the input images [19-21]. The hierarchical structure is constructed by consecutively subsampling the pyramid of two input images. The registration is fulfilled from low to high resolutions in the pyramid. The transformation parameters are searched in the optimization process, starting from the maximum similarity score or minimum difference between the two volumes at the lowest resolu-tion. Then, the parameters obtained from the first (or low-est) resolution level are passed to the next resolution level. The registration is performed until the highest reso-lution level of the pyramid is reached, where the optimal parameter is achieved. As the level increases, the sub-sampling interval decreases, and the accurate registration result is obtained with a higher computational complex-ity. Many toolkit and toolboxes have been progressively developed for the voxel similarity method and for the multi-resolution methods [22, 23]. Hence, the computa-tional complexity of the multi-resolution approach is reduced compared to the original voxel similarity method by using full image content. However, the accuracy of the registration depends on the definition of the level of the pyramid structure. The computational cost for a 3D vol-ume is still an issue for real-world medical image appli-cations.

Equivalent meridian plane (EMP) based MI registra-tion method [24, 25] integrates the feature-based and voxel based methods to register the multi-modal brain volumes, where the volumes are roughly aligned on the basis of the EMP which is determined by principal com-ponent analysis (PCA). Then, the registration is refined by maximizing the MI between the EMP of a float vol-ume and the 2D XY-coordinate plane of the reference volume. Powell’s optimization method is performed for the enhancement of searching during the registration pro-cess. Even though this method is fast thanks to the 2D-plane based registration, the registration result depends on the correctness of EMP. This infers that it cannot guar-antee an optimal solution for every case.

The purpose of this study is to provide a novel method for a rigid registration of 3D CT images. The registration domains in this study are rigid, three-dimensional, and mono-modal images of the same patient. The proposed method aims to combine the advantages of the feature-based and the voxel similarity based methods for the enhancement of the overall performance in the aspects of both accuracy and computational cost. Section II describes the methodology of the proposed method in detail. Experimental results and analysis are presented in section III. Finally, conclusions are drawn in section IV.

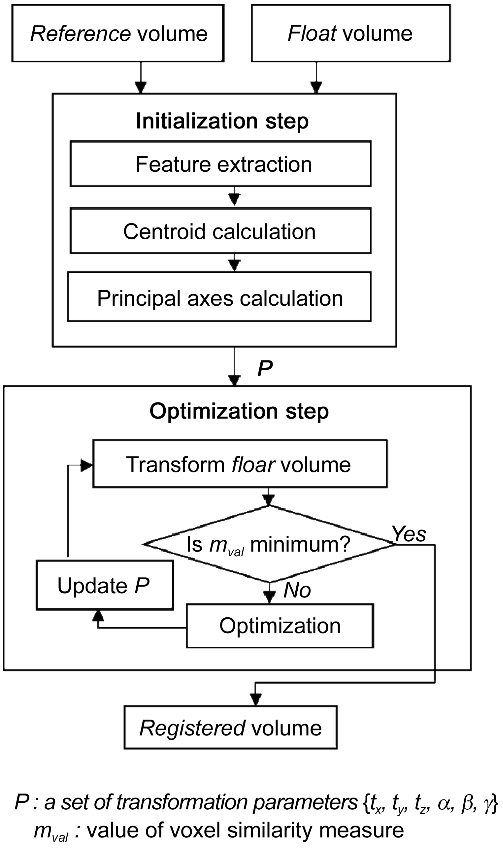
The proposed feature-voxel based image registration method consists of two steps: initialization and optimiza-tion step as shown in Fig. 1. In the initialization step, six transformation parameters are calculated based on the centroid and the principal axes of two CT volumes. The

estimated parameters are passed to the optimization step in order to obtain the optimal parameters. Differing from the previous EMP-MI approach, the proposed method uses the whole 3D volume in order to provide trustworthy registration result. It calculates the NCC score between the reference and the float volume by using the downhill simplex method.

Let V_r and V_f be the reference vol-ume and the float volume, respectively, for registration. As image registration is the alignment of two images into the same spatial coor-dinates, the geometric mapping between the two points x_r ∈ V_r and x_f ∈ V_f can be expressed as,

Where, x_r and x_f denote the 3D coordinates of voxels from V_r and V_f, respectively and M is the geometric trans-formation matrix between them. The type of the transfor-mation matrix M depends on the registration domain. In this paper, the relationship between the two input vol-umes is assumed rigid where the matrix is defined by six parameters which are three translations and three rota-tions. A rigid transformation matrix, M, can be written as the concatenation of a translation vector T(t) and rotation matrix R in the homogeneous coordinates. Thus, M has the form

Hence, the vector representation of a rigid body trans-form of Equation (1) can be rewritten as,

A common way to describe a rotation matrix is the decomposed form of a sequence of the following matrices

Where, α, β, γ represent the Euler angles about the 3D axes, respectively. The rotation matrix can be decom-posed as R = R_γR_βR_α. Thus, the related position between

the reference volume V_r and the floating volume V_f is determined by a set of parameters P = {t_x, t_y, t_z, α, β, γ} in which t_x, t_y, t_z are the translation quanta and α, β, γ are the rotation angles of the floating volume along the 3D axes that is related to the reference volume, respectively. Now, the registration problem for the images that are related rigidly is to find out the optimal parameter set P that best aligns the float volume to the reference volume.

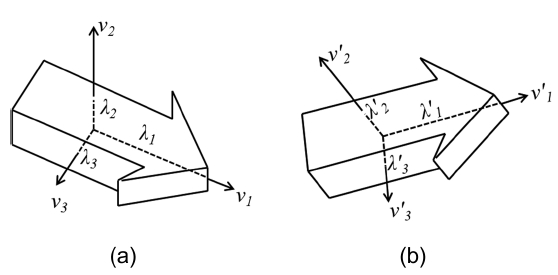
The initial parameters of the two volumes are com-puted based on the transformation of their principal axes. Fig. 2a illustrates a 3D object with its principal axes where eigenvectors, v₁, v₂, v₃, directly represent the orthogonal coordinate system within the object while the correspond-ing eigenvalues, λ₁, λ₂, λ₃, give the information about the length of the respective axes [7]. The rotation of the object is shown in Fig. 2b. Consequently, the rotation of that object is equal to the rotation of its principal axis and translation is the displacement of its centroid. The three steps involved for the extraction of the principal axis of 3D object are: feature extraction, centroid calculation, and principal axis calculation.

A binary volume is used as the feature to represent the geometric shape of 3D to extract the principal axes. Let B(x, y, z) be the binary volume of a 3D volume V(x, y, z) as,

Where, x, y, z represent the coordinates of the image’s voxel and τ is a threshold value that defines the binary volume.

The bone is the most special feature in CT images. Therefore for knee CT registration, the bone region must be extracted from unwanted tissues, such as muscle or fat. The global threshold value, τ, of the bone mask is chosen as 300 Hounsfield units (HU) for the intensity value range of CT image from -1,024 HU to 2,163 HU. Fig. 3b shows the candidate bone region with some resid-uals that are to be removed and holes that are to be filled after thresholding. The residuals are removed by 3D labeling and the holes are filled by the morphological operation. Fig. 3c shows the feature of a bone region that will be used for registration.

The centroid of B(x, y, z) is defined by the mean value of each coordinate point. It is important for the extraction of the principal axes and for the computation of the trans-lations. The centroid C = (x_c, y_c, z_c) is calculated as,

The principal axes of the binary object are defined by the eigenvectors of its inertia matrix [6]. In fact, inertia matrix is the matrix that can be composed by the vari-ances and covariance between the axes. The inertia matrix, I of binary volume B(x, y, z) is given by,

Where,

and

Here, I_xy = I_yx, I_yz = I_zy and I_zx = I_xz. Therefore, the iner-tia matrix, I is real and symmetric. The matrix form of its eigenvectors can be expressed as,

After the three eigenvectors are calculated and form the matrix E, three rotation angles for each principal axis are computed by equating the matrix E to the rotation matrix R (i.e., E = R). The rotation angles α, β, γ can be calculated by using the following equations,

To calculate a set of six parameters P₀ = {t_x0, t_y0, t_z0, α₀, β₀, γ₀} that approximately aligns the floating volume V_f to the reference volume V_r, the centroids and the rotation angles of each volume must be computed first. The calcu-lation is performed by using the following steps:

Step 1: Define the binary volumes B_r and B_f that repre-sents the geometric shapes of V_r and V_f , respectively.

Step 2: Compute the centroid C_r of B_r and C_f of B_f.

Step 3: Calculate inertia matrixes I_r and I_f of their own binary volume B_r and B_f. Then, find the eigenvectors E_r and E_f from their respective I_r and I_f to extract the rota-tion angles.

Step 4: Extract the rotation angles θ_r = {α_r, β_r, γ_r} of V_f and θ_f= {α_f, β_f, γ_f} of V_r by equating E_r and E_f to R.

Step 5: Take the difference of C_r and C_f as T₀ = C_r - C_f, where, P₀ = {t_x0, t_y0, t_z0} is the set of initial translation parameters.

Step 6: Compute the subtraction between θ_r and θ_f as θ₀ = θ_r ？ θ_f, so that a set of rotation parameters θ₀ = {α₀, β₀, γ₀} is achieved.

After the computation of the initial transformation param-eters, which approximately estimates the coarse result to the ideal value, the task that remains is to find out the optimal transformation parameters for the two volumes. The process of finding out the optimal parameters that involves the computation of the voxel similarity mea-sures between the reference and the float volumes. It is followed by the optimization step. The purpose of the similarity measure is to return a value that indicating how matched the two images are [9]. The cost function to determine the optimal parameter matrix is defined by,

Where, S is the similarity metric. The selection of S depends on the number of modalities that are included in the registration or the images’ characteristics. In this paper, the validation of registration is assessed by the cor-relation coefficient between the two volumes as the images to be registered are mono-modality images. Therefore, a NCC is adopted to quantify the degree of the volumes’ similarity in the optimization process. The NCC function is defined as,

Where, n is the total number of voxels, i and j are the voxel indices, V_r(x_i) and V_f(x_j) are the intensity at points x_i and x_j in which x represents x-, y-, z- coordinates of V_r and

represent the mean intensity values and σ_r and σ_f are the standard deviation of the respective vol-umes. They can be computed as,

In principle, the final transformation parameters are considered optimal when the NCC score between V_r and V_f is maximum. However, the sign of the cost function is inverted as in Equation (16), as the downhill simplex optimizer tends to converge to the minimum score. This paper adopts the downhill simplex method as it is a com-monly used and well-defined optimization method. Moreover, it does not require derivative information. The method initializes the optimization process with N + 1 points and it defines an initial simplex in an N-dimen-sional parameter space. This simplex is then deformed iteratively. The simplex is formed by reflection, expan-sion or contraction steps in the iteration to shift the verti-ces of the simplex towards the minimum of the cost function, S. The implementation of a downhill simplex method is based on the algorithm given in [26]. In this work, the simplex is initialized with the six transforma-tion parameters that are obtained from the previous step. This simplex will be iteratively optimized until the score of NCC reaches a minimum. Tri-linear interpolation was used during registration for non-integer grids due to the translation and rotation.

The efficacy of the proposed method is evaluated on both phantom and synthetic data sets. As the purpose of this study is 3D rigid medical image registration, the phantom was simply created in a rigid structure. Fig. 4 describes the phantom that consisting of three erasers inside a box and mounted on a rectangular acrylic plate. The phantom was scanned in a CT scanner provided by Ajou University Hospital, Korea. The reference volume was first scanned without any transformation of the plate. Five floating volumes were obtained by scanning with a random transform of the phantom in x-, y-, z- axes. It is illustrated in Fig. 5. Each CT volume is Digital Imaging

and Communications in Medicine (DICOM) image type. It had a dimension of 512 × 512 × 279 and slice thickness of 1 mm, with a 16-bit depth and 0.6836 mm pixel spac-ing. One particular medical CT volume of knee acquisi-tions was selected for the synthetic data study. We created a database of transformed volume by applying a rigid transformation to it. The knee CT volume had a 16-bit depth, 512 × 512 × 48 in dimensions, 3 mm in slice thick-ness and 0.6836 × 0.6836 mm in pixel spacing. The mag-nitude of the rigid transformations varied between ±10 degree for rotation and ±10 pixel for translation. Within these ranges, 40 volumes were randomly generated to validate the registration.

The proposed method is compared with a voxel simi-larity measure based approach (voxel-based), and a multi-resolution based approach. The voxel-based method establishes a voxel-to-voxel mapping between the refer-ence and the float volume. On the other hand, the multi-resolution registration reduces the computational com-plexity of the voxel-based registration method which is accurate but at the same time it is time-consuming. The 4-level volume pyramid for multi-resolution registration is obtained by resampling both the reference and the float volume along each x, y, z direction. The registration is performed from low to high resolution with the initial values set to one for both the voxel-based and the multi-resolution based methods. For a comparison purpose, NCC and the downhill simplex method are adopted in both methods and the proposed method. The downhill simplex method was implemented in C function and

called from the MATLAB (MathWorks, Natick, MA, USA) as mex file. The remaining parts of the programs were implemented in MATLAB 7.11 and they run on a PC with Intel® Core™ i7, 2.67 GHz processor and 8 GB RAM. The registration time, excluding the time of the loading data sets, is in seconds.

NCC scores between the reference and the registered volumes are computed for the evaluation of the accuracy of the proposed method on phantom images. The closer the score is to one, the higher the accuracy of the registra-tion of the two volumes. In the case of synthetic image registration, the accuracy is measured by the mean and standard deviation in the differences between the com-puted transformation parameter values (P) and the ground-truths. The lower the mean and the standard deviation in the differences, the higher is the accuracy.

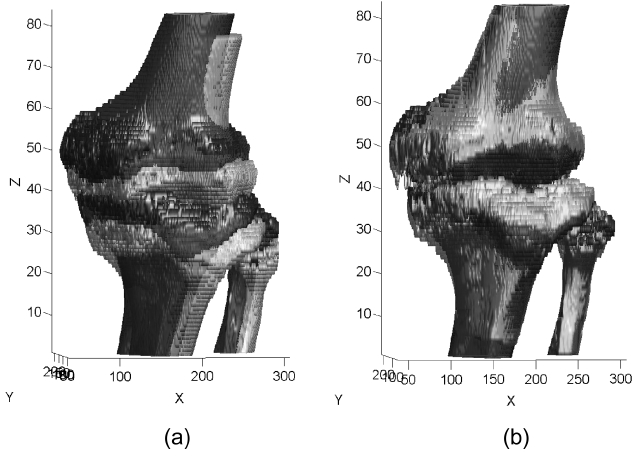
Registration of the phantom is performed while setting up the first scan as the reference volume and the remain-ing five scans as float volumes. The reference volume is named as set_1 and the remainders are serially named as set_2 to set_6. In order to accomplish registration, the appropriate volume of interest (VOI) is selected from both the reference and the float volumes. The size of VOI for each volume is 231 × 131 × 111 and the registration process is taken on those VOIs. Fig. 6a and 6b show slices of VOI of the original reference and float volumes. For the phantom study, the binary volume which is needed for the extraction of the principal axes is simply obtained by using Otsu [27] thresholding method that is followed by 3D labeling. Otsu’s method [27] is a non-parametric and unsupervised method that provides an automatic global threshold value τ in Equation (4). Fig. 6c and 6d shows the binary results after the application of the Otsu’s method [27]. Some unwanted residual remains apart from the desired region. Those residuals are removed by labeling the connected component of the 3D binary volume. Fig. 6e and 6f show the binary volumes that are ready to extract the principal axes, after the labeling pro-cess. Fig. 6g and 6h show slices of the segmented regions for reference and float volumes, respectively.

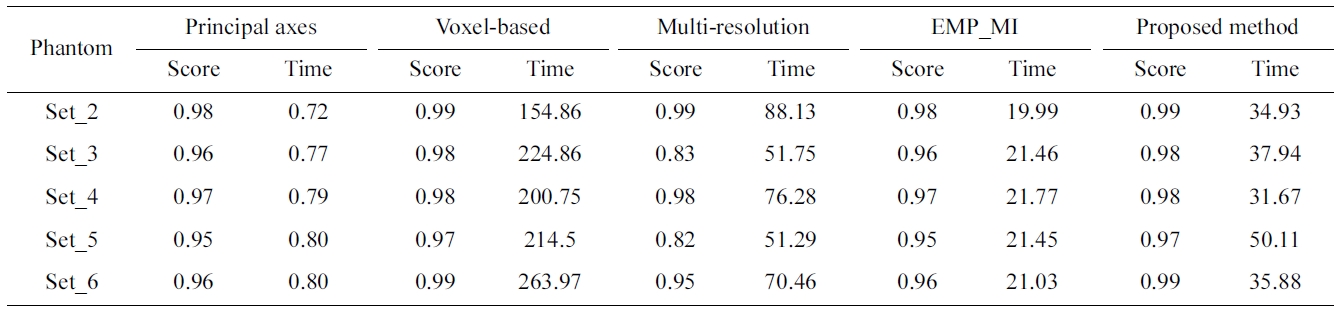
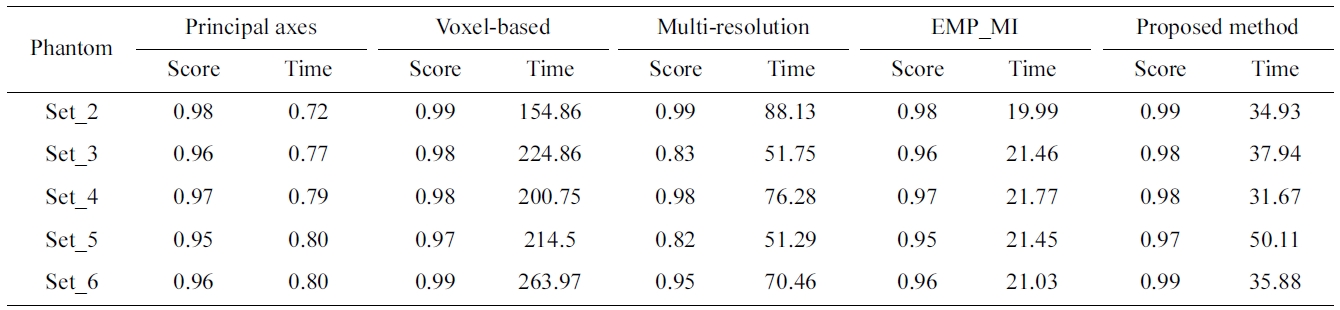
The superimposed 3D visualization of the registration results for the reference (set_1 in dark gray) and the float (set_6 in light gray) volumes are presented in Fig. 7. Table 1 compares the NCC score and the processing time of the proposed method against the principal axes based approach, the voxel-based, the multi-resolution based method and EMP based MI method.

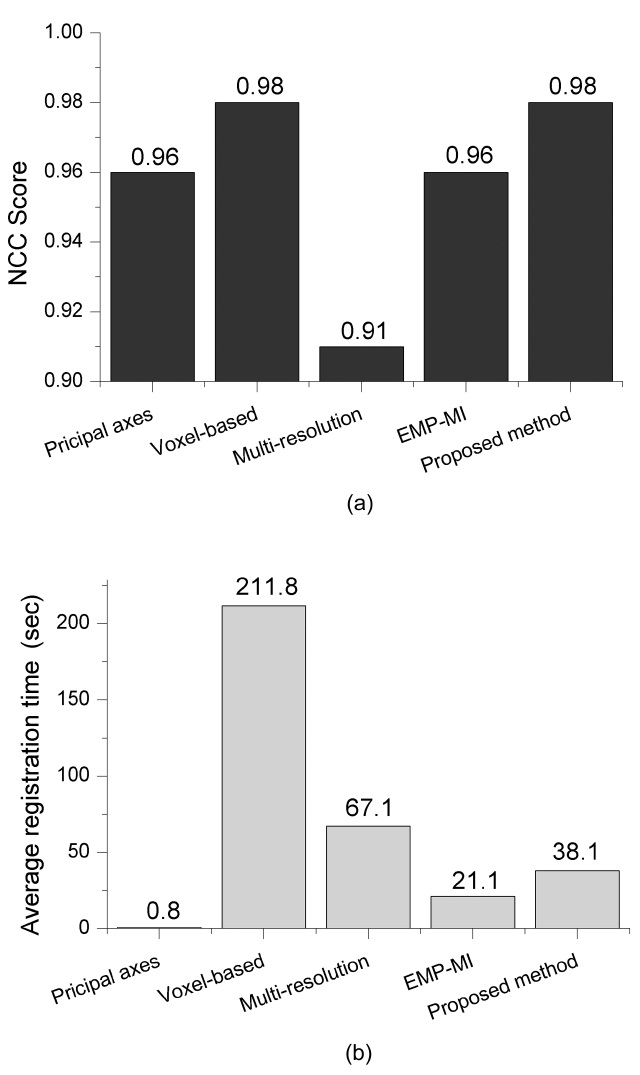
The average NCC score and registration time are illus-trated in Fig. 8. The figure reveals that the voxel-based approach provides high accuracy result with high compu-tational complexity. Multi-resolution based approach reduces the computational cost but the average NCC is low. This implies that it may produce unsatisfied results.

Both the principal axes based approach and the EMP-MI based approach provide a fast processing time result but a low correlation score is obtained. Although the proposed method is not as fast as the other two methods, it provides

efficient registration result as the average NCC score is as high as the voxel-based method. Moreover, Table 2 describes the before- and after-registration score of dif-ferent similarity measures for each phantom data set.

As NCC, the higher the score of NMI, the higher is the accuracy of the registration. In contrast to NCC and NMI, the higher accuracy of registration is obtained when the score of SSD is small. To evaluate the proposed method with different similarities, the correlation score of the ref-erence (set_1) and the registered volume which is trans-formed the float volume (set_2-set_6) by the parameters resulted from different similarity measures. The average correlation score of NCC and NMI is 0.98 and the aver-age correlation of SSD is 0.96. The average registration time of NCC is 38.1 seconds, while those of NMI and SSD are 53.2 and 23.7 seconds, respectively. Therefore, NCC provides the similar average score with NMI, higher score of SSD and it acquires a faster average regis-tration time.

The registration is also evaluated on the synthetic datasets that are randomly generated by rotating and translating one knee CT volume along the x, y, z axes within the given ranges. The appropriate 307 × 231 × 84 VOI size of the CT image is selected for registration.

A set of new float images were created by the applica-tion of the random rigid transformation with a rotation that varies from -10 degree to +10 degree and a transla-tion which varies from -10 pixels to +10 pixels along all the axes. As the registrations are performed with the ground-truths, the accuracy is evaluated by the mean and

standard deviation (SD) of rotation and translation errors. Standard deviation shows the amount of variation from the mean. The smaller the standard deviation, the higher is the accuracy of registration. Table 3 shows the mean (SD) of the transformation errors and the average pro-cessing time in the registration of the set of new float images with the reference images by different approach. Although the processing time of the principal axes based approach and the EMP-MI based approach is faster than the voxel-based, multi-resolution based and the proposed methods, they provide a big mean (SD) value of synthetic data sets. The proposed method provides more accuracy result and relevant processing time of registration. Fig. 9 shows the registration result of one of the synthetic data sets.

This paper presents a novel method to automate the process of registering 3D CT images taken at different instances. The proposed two-step method first finds out the initial transformation parameters based on the princi-pal axes of the binary structure of the input images. The parameters acquired in the first step are then optimized to provide the parameters that best align the float volume to the spatial coordinates of the reference volume. The objective of this preliminary study using phantom and synthetic data is to validate the performance of the pro-posed method in terms of accuracy and processing time. The experiments on phantom and synthetic data show that the algorithm provides robust and faster results com-pared to the voxel similarity measure based approach and the multi-resolution registration method. The experimen-tal results demonstrated that the proposed method can be applied for the rigid registration of real images. In future, real patient data sets are to be examined. Further, a more robust segmentation method is to be employed to obtain better results for the patient images, as the current corre-lation calculation is limited only to the bone region.