



Multicore processors have become the mainstream computing platform due to their advantages of high paral-lelism and low power consumption. Following the adop-tion of multicore processors in desktop and server domains,multicore processors have also been used in embedded systems. In particular, with an increase in the demand for high performance by high-end real-time applications such as HDTV and real-time multimedia processing applica-tions, multi-core processors are expected to be increas-ingly used in real-time systems. In the near future, researchers have envisioned a possible deployment of real-time systems on large-scale multi-core processors that are composed of tens or even hundreds of cores on a single chip [1].
Real-time systems can be classified into hard real-time systems and soft real-time systems by the characteristics of the timing constraints. In hard real-time systems, it is critical to accurately obtain the worst-case execution time (WCET) for each task and this provides the basis of task scheduling. As an inaccurate WCET will lead to an inap-propriate task scheduling paradigm of a real-time system, this can degrade the quality of service or even result in the failure of a system. In addition to estimating the WCET accurately, it is also desirable to optimize real-time code to reduce WCET. Better WCET of a task offers the real-time scheduler more flexibility to schedule this task for meeting its deadline. Moreover, among the other benefits, reducing WCET of a computing task can help to conserve the power that is used by the system [2]. The basic idea is that with WCET, information is available and if a task still has slacks then the clock rate can be lowered in order to reduce the power dissipation while at the same time meeting the deadlines.
In order to reduce the WCET of real-time tasks (i.e., to obtain “better” WCET), code positioning approaches have been proposed [3, 4]. However, current WCET-oriented code positioning approaches center on the enhancement of the WCET of single-threaded application on unipro-cessors. This cannot be effectively applied to multicore processors with shared caches. This is due to these code positioning algorithms [3, 4] which only reduce the intra-thread cache conflicts but cannot detect the inter-thread cache conflicts or avoid them. Furthermore, these approaches may reduce the intra-thread L1 cache misses at the cost of more inter-thread shared L2 cache misses, whose penalty is usually much more than that of an L1 cache miss. Thus it may hurt the overall performance. Therefore, it is cru-cial to develop multicore-aware code positioning tech-niques for real-time applications that run on multicore platforms.
In this paper, we assume that two real-time threads are running concurrently on a dual-core processor with a shared L2 cache. Our goal is to reduce the WCET of these threads (in some applications with mixed real-time and non-real-time tasks, a real-time thread may run con-currently with a non-real-time thread. However, it should be noted that code position for this scenario is actually less challenging, as the performance of the non-real-time thread can be sacrificed for the enhancement of the WCET of the real-time thread [5]. Whereas in this paper, the WCETs of both the real-time threads are to be consid-ered.). We have studied three approaches: a worst-case-oriented (WCO) approach, and two fairness-oriented approaches, including the percentage-fairness-oriented (PFO) and amount-fairness-oriented (AFO) schemes. All these approaches are built upon multicore cache WCET analysis but with different optimization goals (prelimi-nary work of this project was published in a conference paper [6]. In this paper, we have explored the effective-ness of the code co-positioning strategies with different cache sizes and memory latencies and they are likely to become important for future multicore/manycore proces-sors). Our experiments show that all these three proposed techniques can effectively reduce the WCET for co-run-ning real-time threads in order to achieve their respective optimization goals.
The rest of the paper is organized as follows. Section II reviews related work. Section III describes the proposed multicore-aware code positioning approaches. The evalu-ation methodology is explained in Section IV and the experimental results are presented in Section V. Finally, the conclusions are made in Section VI.
Code positioning is a software optimization that is done by the compiler to reorder or position the structural units (e.g., a basic block or a procedure) within a program. As some processors induce a pipeline delay that is related to the transfer of control, these delays are more common in embedded systems. They do not have branch predic-tion and target buffers to reduce the complexity of the processor. The compiler attempts to position the basic blocks to minimize the number of both the unconditional jumps and taken branches to reduce the pipeline delays. Furthermore, for the processors with instruction caches, code positioning can help to improve the instruction cache locality and reduce cache miss penalties. Traditional code positioning algorithms mostly aim at the enhancement of the average-case execution time (ACET) by reordering the basic blocks to make the most frequently traversed edges that are contiguous in memory [7-11]. However, as the most frequently traversed edges may not be a part of the worst-case paths, the WCET cannot be guaranteed to be reduced by these approaches. Even if the WCET path is taken into account by the code positioning algorithm, a change in the positioning may result in a different path which becomes the worst-case path.
In order to improve the worst-case performance in a processor with instruction caches, a code positioning approach is proposed. It is done to focus on positioning the basic blocks on the worst-case path in the program and to reduce the pipeline delay that is caused by the transfer of controls [3]. The main idea of this basic block positioning algorithm is to select the edges between the basic blocks on a worst-case path to be contiguous and this will minimize the WCET. Recently, another WCET-oriented approach is proposed to reduce the number of cache conflict misses by means of placing procedures that contribute to the WCET, so that they are mapped contiguously in memory layout to avoid the overlapping of cache lines belonging to a caller and a callee procedure [4]. However, both of these approaches have not consid-ered the inter-thread cache conflicts in multicore comput-ing platforms.
Cache partitioning is another useful method to isolate tasks in a multitasking real-time system to allow individ-ual analysis of cache behavior. Thus, it enhances the time predictability of each task. There are mainly two types of cache partitioning approaches, i.e., hardware-based [12, 13] and software-based [14, 15]. In hardware-based cache partitioning, address mapping hardware is inserted into the processor along with a cache to restrict cache accesses to a single contiguous cache segment at any one time. Therefore each task has the right to access a private cache segment for one or more partitions. In contrast, the software-based approach can provide more flexibility and possibly better performance over the hardware-based cache partitioning. It creates a private cache partitioning for each task by assigning it a separate address space in the cache with the use of a compiler and a linker. Thus, it can provide a large number of independent cache parti-tions at no additional cost with good flexibility. Our mul-ticore-aware code positioning techniques proposed in this paper are complementary to the cache partitioning approaches. Multicore-aware code positioning enables different tasks to the share caches still for the achieve-ment of benefits such as efficient cache space usage, low-cost cache coherency and easy sharing [16] while mini-mizing the inter-core cache conflicts. Moreover, as a pure software-based technique, multicore-aware code posi-tioning does not need to modify the hardware while achieving “better” WCET for real-time tasks that run on multicore processors.
In a multi-core processor, each core typically has pri-vate L1 instruction and data caches. The L2 (and/or L3) caches can be either shared or separated. While private L2 caches are more time-predictable that is there are no inter-core L2 cache conflicts, they suffer from other defi-ciencies. First, each core with a private L2 cache can only exploit separated and limited cache space. Due to the great impact of the L2 cache hit rate on the performance of multi-core processors, private L2 caches may have worse performance than a shared L2 cache with the same total size as each core with shared L2 cache may make use of the aggregate L2 cache space more effectively. Besides, separated L2 caches increase the cache synchro-nization and coherency cost [16]. Moreover, a shared L2 cache architecture makes it easier for multiple coopera-tive threads to share instructions and data. This becomes more expensive in separated L2 caches [16]. Therefore, in this paper, we will study the WCET analysis of multi-core processors with shared L2 caches.
For simplicity, in this study, we assume that two real-time threads run concurrently on different cores of a dual-core processor with private L1 caches and a shared L2 cache but our techniques can be applied or adapted for multiple threads that run on multicore chips with multi-level memory hierarchies. We have proposed three strate-gies in order to optimize the WCET of both the threads for making different tradeoffs. These strategies include a WCO strategy and two fairness-oriented strategies that include both AFO and PFO. The WCO aims at the improvement of the performance of the real-time thread with the longest WCET, as this type of thread mostly impacts the performance of the whole system. By com-parison, AFO and PFO attempt to treat all the real-time threads fairly, and their goals are to reduce the worst-case performance of each concurrent real-time thread by approx-imately the same amount or percentage, respectively.
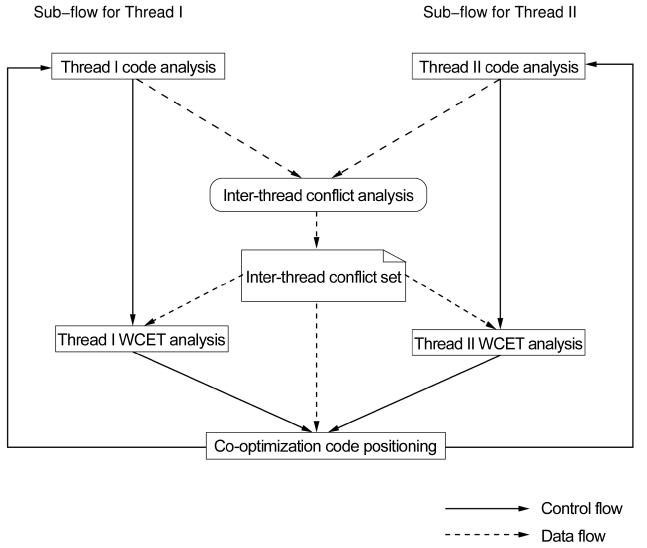
Fig. 1 depicts the main working flow of the WCET-ori-ented co-optimization architecture and it mainly consists of two sub-flows. The sub-flows of both the threads are initialized with code analysis that includes control flow analysis and static cache analysis. The inter-thread cache conflict analysis algorithm calculates the worst-case inter-thread L2 cache conflict set. According to the inter-thread L2 cache conflict set, the programs of both the threads are positioned following the assigned strategy to reduce the inter-thread L2 cache conflicts for attaining different optimization goals. After the code positioning phase, the WCET analysis is conducted to find out the new WCETs for both threads. They are compared with their original WCETs for guiding the co-optimization. It is worthy to note that the flow of both threads from code analysis to code positioning may be repeated for several times for the achievement of optimal results.
>
B. Worst-Case-Oriented Code Positioning
The objective of WCO is to minimize the longest WCET of both the real-time threads (i.e., reducing the worst-case WCET of co-running threads), whose algo-rithm is described in Algorithm 1. The inputs of the algo-rithm are the two programs that are to be optimized. In line 2, the termination variable that finishes the repetitive
optimization process is initialized. In the next three lines, fundamental data that are required by the algorithm are calculated for both the programs. This includes the origi-nal WCETs for both the programs and the L2 cache con-flict instruction list. After the completion of the initialization phase, the original WCETs of both the programs are com-pared with each other in the core of the algorithm from line 6 to 26. Then, the program with a smaller original WCET will be positioned for the optimization of the WCET of the other program maximally. As shown from line 7 to line 15, in case that the original WCET of P1 is larger than that of P2, program P2 will be positioned at line 8, in which the conflict instructions from P2 that lead to the largest inter-thread cache conflicts will be allocated at new memory addresses. These memory addresses map to L2 cache blocks with the minimal conflicts and the corresponding instructions from P1. It should be noted that in a virtual memory system, this memory address re-mapping can be easily implemented by the updation of the virtual-to-physical address mapping information in the page table and TLB. The WCETs of both the programs will be analyzed again when the positioning of P2 finishes at lines 9-10. If the WCET of P1 is still larger than that of
[Algorithm 1] WC_Oriented_Code_Positioning

WC_Oriented_Code_Positioning
P2, then the termination variable will be assigned true, else the function of
>
C. Fairness-Oriented Code Positioning
While WCO focuses on the optimization of a single thread that has the worst WCET among the co-running threads, FO code positioning needs to optimize all the co-running threads to ensure fairness. As the WCETs of both threads may vary significantly, the “fairness” has differ-ent meanings and implications. This depends on the opti-mization objectives. In this work, the FO strategy is divided into two different schemes according to the “fair-ness”goals and it includes 1) reducing approximately the same amount of WCET, or 2) reducing approximately the same percentage of WCET. Accordingly, these two schemes are named AFO code positioning and PFO code positioning, respectively.
1) Amount-Fairness-Oriented Scheme
AFO code positioning algorithm aims at the reduction of the WCETs of both the co-running threads by approxi-mately equal amount. When the WCO code positioning approach is applied, only the instructions of the thread with shorter (i.e. “better”) WCET are positioned to reduce the WCET of the other thread maximally. In this case, the amount of WCET is reduced by avoiding the inter-thread L2 cache conflicts which is the same to both threads. However, the difference in the amount of WCET reduc-tion can be caused by different intra-thread L1 and L2 cache misses due to the WCO code positioning. There-fore, AFO can leverage WCO to decrease the inter-thread cache misses, while it tries to recover some of the posi-tioned instructions in WCO. This is done by a process named code
The algorithm of AFO is demonstrated in Algorithm 2. The inputs and the initialization phase are the same as those of WCO. In line 6, the WCO algorithm is invoked to reduce the inter-thread L2 cache misses. In this algo-rithm, P2 is assumed to be the thread with a larger WCET. Therefore, only the instructions from P1 are posi-tioned by WCO. In the core of this algorithm, some posi-tioned instructions of P1 are recovered to their original positions by de-positioning at line 8. The corresponding instructions from P2 are positioned instead to avoid the inter-thread L2 cache conflicts at line 9. Then, the present WCETs of both programs are computed at lines 10 and 11
[Algorithm 2] AF_Oriented_Code_Positioning

AF_Oriented_Code_Positioning
through WCET analysis. It is based on which the differ-ence of WCET reduction of both programs (i.e., Δ
2) Percentage-Fairness-Oriented Scheme
While AFO targets approximately the same amount of WCET reduction, PFO aims at about a similar percentage of WCET reduction. The principle of PFO code position-ing is described as follows. In the multicore processor with shared L2 cache, the WCET of one thread can be broken into the computation time by assuming perfect caches namely, the L1 cache miss penalty and the L2 cache miss penalty. The L2 cache miss penalty consists of two parts: 1) the intra-thread L2 cache miss penalty caused by L2 cache conflicts between instructions from the same thread and 2) the inter-thread L2 cache miss penalty due to the cache conflicts between the instruc-tions from different threads that share the L2 cache. The WCET of one thread can be calculated by Equation 1,where
After code positioning, the inter-thread cache conflicts will be decreased. However, the intra-thread cache con-flicts may increase both on L1 and L2 caches. As the computation time
As the goal of PFO code positioning is to maximally reduce the WCET of each real-time thread by an approxi-mately equal percentage. Assume that there are two threads, i.e., Thread
As the execution time
Algorithm 3 illustrates the algorithm of PFO code positioning approach. The inputs of the algorithm are the two programs that are to be optimized. In line 2, the ter-mination variable that completes the optimization is ini-tialized. In the next three lines, the original WCETs of both programs are calculated and the L2 cache conflict instruction list is also determined. In the core of the algo-rithm from line 6 to line 19, firstly the instructions that are required to be positioned for both programs are iden-tified according to the designing principle of PFO that was aforementioned. Then both programs are positioned at line 9 and line 10. From line 11 to line 12, the WCETs of both programs are analyzed again after code position-ing. Based on the original WCETs and new WCETs of both programs, the WCET percentage variance between these two programs is calculated. This is done to deter-mine whether or not the WCET percentage variance after code positioning process is smaller than the original WCET percentage variance at lines 13 and 14. If this is true, then the original WCET percentage variance Δ
[Algorithm 3] PF_Oriented_Code_Positioning

PF_Oriented_Code_Positioning
>
D. Inter-thread L2 Cache Conflict Analysis
In the co-optimization architecture depicted in Fig. 1, inter-thread L2 cache conflict analysis is an important step to identify the worst-case inter-core L2 cache con-flicts and the associated instructions from different cores. This provides the inter-thread L2 cache conflict set to code positioning algorithms. We propose to leverage Yan et al.’s recent work in [17] to analyze the worst-case inter-thread L2 cache conflicts. The main steps of this algorithm are described in Algorithm 4.
The inputs of this algorithm are the programs from both the co-running threads. Initially, the L2 cache status sets for only one thread alone (i.e., without considering inter-thread conflicts) and they are calculated for both threads. This identifies the groups of instructions within the same thread that share the same cache lines. In order to find out the worst-case inter-thread instruction interfer-ences from two different threads, we distinguish instruc-tions in loops from those that are not in loops. Each instruction from each thread is examined, whose L1 cache access behavior can be easily obtained by using static analysis techniques for instruction caches (line 5-6) [17].
If there exists an L1 miss, then it is checked where this miss happens (line 7), i.e., in or out of loops. If this miss occurs in a loop, then it is necessary to determine whether or not the cache line used by this instruction will be occu-pied by the instructions from the other thread, and whether those instructions are also in a loop or not. The cache line used by this instruction from Thread
[Algorithm 4] Inter_Conflict_Analysis

Inter_Conflict_Analysis
loop or not at line 10. If the conflicting instruction hap-pens to be in a loop as well, then the worst-case number of conflicts of these conflicting instructions is equal to the smaller one of the worst-case number of access times from these two threads (line 11). This can be obtained from control flow analysis.
The inter-thread L2 cache conflict set is constructed in the format of a matrix. In this type of matrix, a row index represents the instruction number from Thread
The WCET of a real-time task is computed by using the implicit path enumeration technique (IPET) proposed by Li and Malik [18, 19]. In IPET, the WCET of each task is calculated by maximizing the objective function in Equation 5 where,
When an instruction runs in a multi-core processor with a hierarchical cache memory, its execution time depends on whether the instruction access results in a cache hit or a cache miss. Therefore, the total execution time of a program is heavily influenced by the number of cache misses and the penalty of cache misses. The state of L1 instruction cache accesses for each thread running on a multi-core processor with a shared L2 cache can be derived by using static cache analysis. Moreover, the state of L2 instruction cache accesses for each basic block includes the potential inter-thread L2 cache con-flicts. It can be computed by using the inter-thread L2 cache conflict analysis algorithm that is depicted in Sec-tion III-D. Therefore, the total number of cache misses can be calculated in Equation 7. Where,
Equation 8 integrates the penalty of cache misses into the objective function to accurately compute the WCET of the whole program. In this equation,
As a result, the WCET of the real-time thread can be calculated by using an integer linear programming (ILP) solver in order to maximize the objective function in Equation 5.
We evaluate the proposed multicore-aware code posi-tioning schemes on a heterogeneous dual-core processor with a shared L2 cache. In order to achieve better perfor-mance, energy efficiency and low cost, embedded appli-cations have increasingly used heterogeneous systems. This includes multiple programmable processor cores, specialized memories and other components on a single chip [20]. For instance, most of the hand-held devices now adopt a heterogeneous dual-core architecture that is composed of a digital signal processing (DSP) core and an advanced RISC machines (ARM) core. In this paper, we focus on the evaluation of the multi-thread code posi-tioning on a heterogeneous dual-core processor that con-sists of a very long instruction word (VLIW)-based DSP core and a general-purpose core. The VLIW core is based on the Hewlett-Packard Lab PlayDoh (HPL-PD) 1.1 architecture [21] and the general-purpose core is similar to the Alpha 21264 processor [22]. More specifically, the simulation tools of Trimaran [23] and Chronos [24] (including SimpleScalar [25]) are extended to simulate this framework. The front end of Chronos compiles the other thread benchmark into common object file format (COFF) format binary code by gcc compiler. This is tar-geted to SimpleScalar. By disassembling the binary code, the global control-flow graph (CFG) and the related information of instructions are acquired by Chronos front end. Hence, it helps in the static cache analysis. A com-mercial ILP solver-CPLEX [26] is used to solve the ILP problem to obtain the estimated WCET.
Without losing generality, we assume a dual-core pro-cessor with two-level cache memories. Each core has its own L1 instruction cache and L1 data cache. Moreover, both cores share the same L2 cache in order to utilize the aggregate L2 cache space. Note that multicore processors can also use separated L2 caches to achieve better time predictability. However, a shared L2 cache has a few important advantages such as fast data sharing, reduced cache-coherency complexity and false sharing and possi-bly superior cache performance [16]. In order to limit the scope of this study and to focus on instruction cache anal-ysis, the L1 data cache of each core is assumed to be per-fect. In order to compare the worst case performance with an average case performance in the heterogeneous dual-core processor, the memory hierarchy of SimpleScalar simulator is integrated into a Trimaran’s memory hierar-chy and the core of SimpleScalar is linked to Trimaran’s simulator by means of multi-thread programming. There-fore, an environment where two threads can run at the same time on different cores with a shared L2 cache has
[Table 1.] Basic configuration of a simulated heterogeneous dual-core processor

Basic configuration of a simulated heterogeneous dual-core processor
[Table 2.] Estimated and simulated worst-case performance results of the baseline scheme
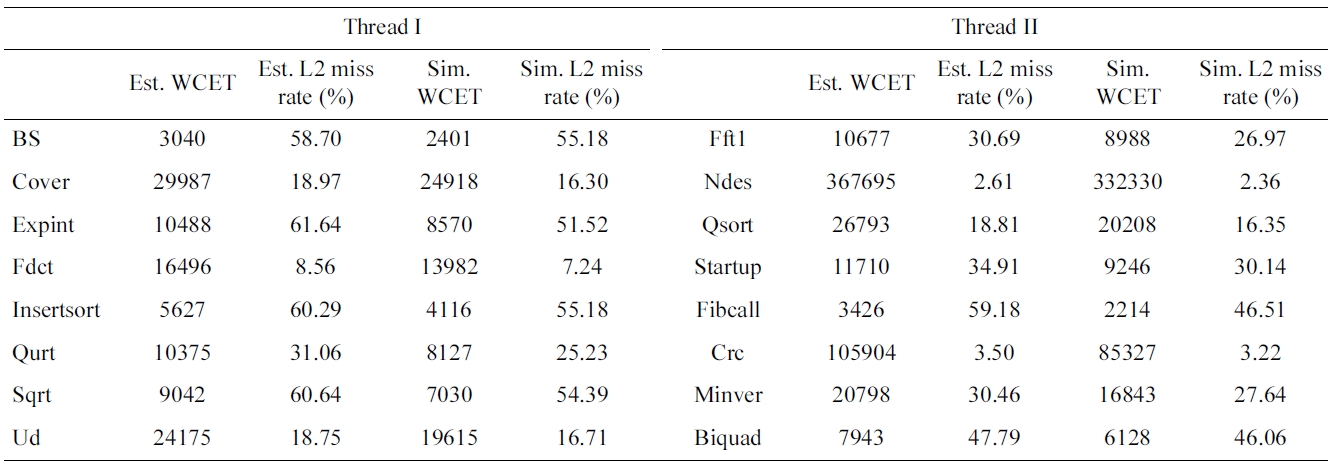
Estimated and simulated worst-case performance results of the baseline scheme
been simulated. The basic configuration of a simulated hybrid dual-core processor is shown in Table 1.
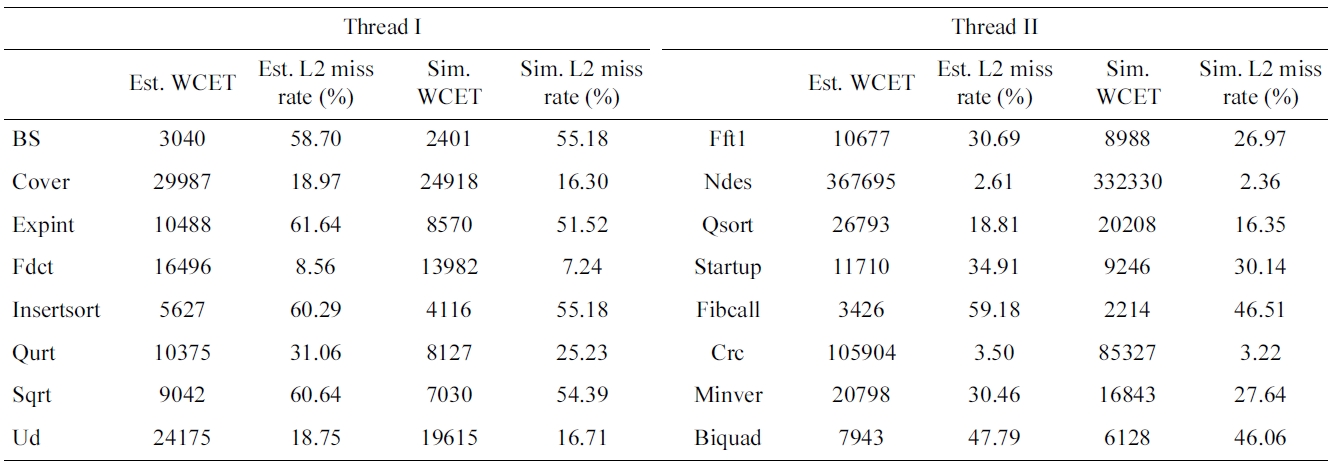
In our experiments, we choose sixteen benchmarks from Malardalen WCET benchmark suite [27] and based on them we form eight benchmark pairs by selecting a thread from each group as shown in Table 2. The perfor-mance results of WCO code positioning, PFO code posi-tioning and AFO code positioning are compared with the obtained baseline performance results. In this no code positioning approach is applied.
>
A. Performance Results of WCO
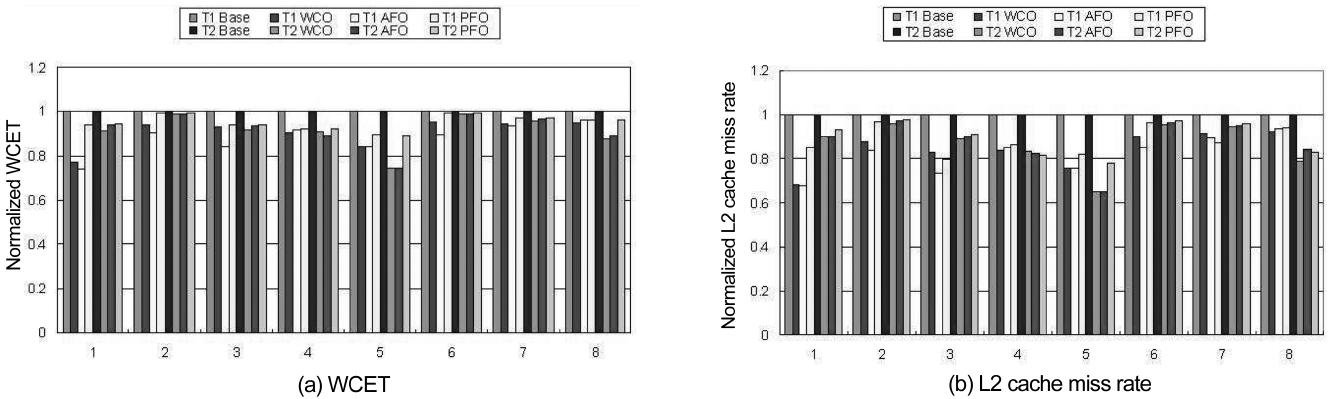
Fig. 2a compares the WCETs of eight benchmark pairs between the WCO scheme and the baseline scheme. They are normalized with respect to the results of the baseline scheme. We can clearly see that the WCO scheme can decrease the WCET for all the threads as reducing the inter-thread L2 cache misses benefits of both threads. The percentages of WCET reduction for those eight bench-mark pairs ranges from 1.14% to 15.85% and they depend on how much percentage the inter-thread L2 cache miss
penalty takes in the WCET of each thread.
The variation of L2 cache miss rate of these bench-marks can be seen in Fig. 2b. For the WCO scheme, it is likely that the thread with the longest WCET is not posi-tioned, as the WCET of this thread is much larger than that of the other thread. In this case, the L2 cache miss rate of this thread with the longest WCET can be reduced more by the WCO scheme than both the PFO or AFO schemes as no additional intra-thread L1 cache misses and intra-thread L2 cache misses will occur in this thread with the WCO scheme. For instance, in benchmark pair 3 both the WCET and L2 cache miss rate of benchmark Qsort in the WCO scheme are lower than those of the PFO and AFO schemes. On the other hand, its counter-part benchmark Expint has higher L2 cache miss rate and larger WCET in the WCO scheme than those of the AFO scheme (which has better results than PFO). We also notice that for the benchmark pair 5, L2 miss rates and WCETs of both threads are adequately reduced by all the three schemes. This is due to the difference between the original WCETs of both benchmark pairs is relatively small and the L2 cache miss penalty takes a large fraction of their respective WCET.
>
B. Performance Results of PFO
The performance results of the PFO code positioning approach are also demonstrated in Fig. 2. It indicates that this approach can reduce the WCETs of both the threads within a benchmark pair by approximately equal percent-ages. For example, the difference of WCET reduction percentage for benchmark pair 2 that consists of Cover and Ndes is only 0.03%. Even for the worst case, the dif-ference between WCET optimization percentage for benchmarks Insertsort and Fibcall is just 0.64%. On an average, the variation of WCET optimization per-centage for these eight benchmark pairs is only 0.29%.
However, we also find out that the percentage of WCET reduction by PFO varies much across the differ-ent benchmark pairs. For example, the WCET of the first benchmark pair is reduced by more than 5%, while the percentages of WCET reduction for benchmark pairs 2 and 6 are just about 1%. This is due to the effect of the PFO approach on WCET reduction is mainly determined by two factors. First, to ensure fairness of WCET optimi-zation, a wide discrepancy between the original WCETs of both threads limits the degree of WCET improvement for both benchmarks, for instance the benchmarks in pair 2 and pair 6. Second, the percentage of inter-thread L2 cache miss penalty in the original WCET is another important factor for the determination of the WCET enhancement through code positioning. Generally, if this percentage is higher, then there is more room for poten-tial WCET enhancement. The first factor also leads to another conclusion that the PFO approach is generally worse than the other two approaches in terms of the reduction in the worst-case execution time (i.e., achiev-ing “better” WCET). This can be observed in Fig. 2 in case of both WCET and L2 cache miss rate. In other words, while the PFO approach can achieve fairness in terms of the percentage of WCET optimization for co-running threads, it indeed compromises the efficiency of WCET optimization as compared to WCO and AFO.
>
C. Performance Results of AFO
Fig. 2 also illustrates the normalized WCET and L2 cache miss rate in case of the AFO scheme with respect to the Baseline Scheme. The AFO scheme can not only reduce the WCET and L2 cache miss rate for both threads in each benchmark pair, but it can also achieve the fair-ness in terms of the amount of WCET reduction. More-over, the differences in the reduced WCETs between both benchmarks only range from 4 cycles to 120 cycles across all pairs. On an average, the difference of WCET reduction is only about 80 cycles. This is less than the latency that incurred from one L2 cache miss indicating that the fairness in terms of the amount of WCET reduc-tion between co-running threads is achieved.
Interestingly, when we compare AFO with WCO (note that PFO in general is inferior to both AFO and WCO as aforementioned), we find out that for all benchmark pairs, while WCO can decrease the WCET for one thread more than AFO, AFO can often reduce the WCET of the other thread (in the same pair) more than WCO. The rea-son is that the AFO approach does not position some of the instructions of the thread that would be aggressively positioned by the WCO approach for reducing the inter-core L2 cache misses. This often leads to an increase of intra-core L2 cache miss on one thread while it leads to a decrease of it on the other thread. As an example, in the first benchmark pair, the benchmark Fft1 gets 2.14% improvement on WCET in the WCO scheme than in the AFO scheme. However, the WCET of BS in the AFO scheme is about 3.29% and it is better compared to the WCO scheme. Therefore, we believe AFO is comparable to WCO in terms of WCET optimization, while achiev-ing fairness in terms of the amount of WCET reduction by considering both the co-running threads.
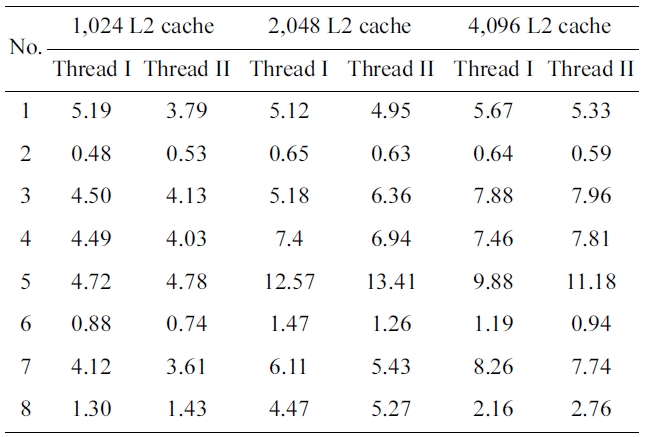
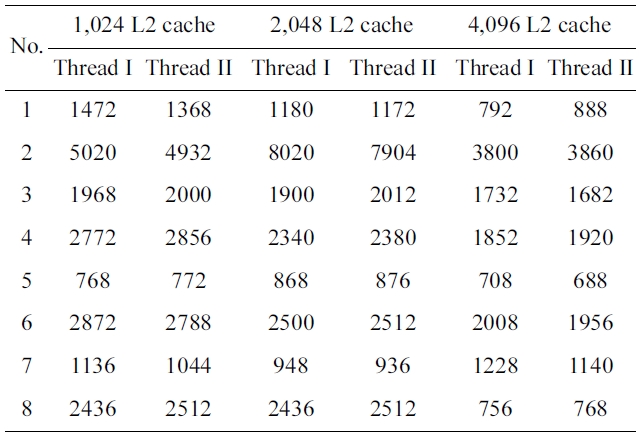
We have also made experiments to study the effects of the code positioning approach with the different L2 cache sizes. Table 3 shows the performance optimization per-centage in the PFO scheme as the L2 cache size increases from 1,024 bytes to 2,048 bytes and 4,096 bytes, while the L1 cache size of both cores is kept to 128 bytes. As one can expect, PFO strategy makes both threads gain the approximated optimization percentages in all these three cache models. With 1,024 bytes L2 cache configuration, the average variation of the optimization percentages is nearly 0.5% and the maximum value of the optimization percentage difference is only 1.3%. The average value is
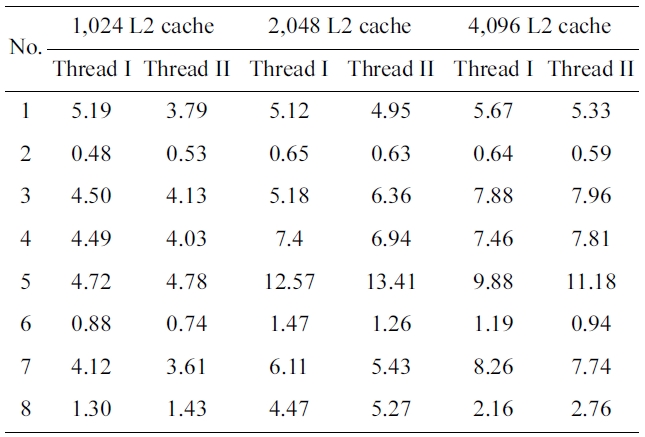
Worst-case execution time optimization percentage of percentage-fairness-oriented scheme with respect to the baseline scheme with L2 cache size ranging from 1024 bytes to 2048 bytes and 4096 bytes
almost 0.43% in case of 4,096 bytes L2 cache. In princi-ple, the performance optimization percentage will increase with an increase of the cache size, as there are possibly more free memory spaces where more conflicting instruc-tions can be positioned. This is proved by the results of several benchmark pairs in the cache size sensitive exper-iments. For example, the average percentage of WCET improvement of benchmark pair 5 increases from 4.75% to 8.2%, and 10.53%, when the size of the L2 cache increases from 1,024 to 2,048, and 4,096 bytes, respec-tively. However, the average percentage in the results of some benchmark pairs does not vary much with the varia-tion of the L2 cache size. However, for benchmark pair 2 the average optimization percentage only ranges from 0.455% to 0.64% and it does not increase strictly propor-tional to the size of L2 cache. This exceptional result may be caused by the fact that the benchmark is not sensitive to this scope of the cache size.
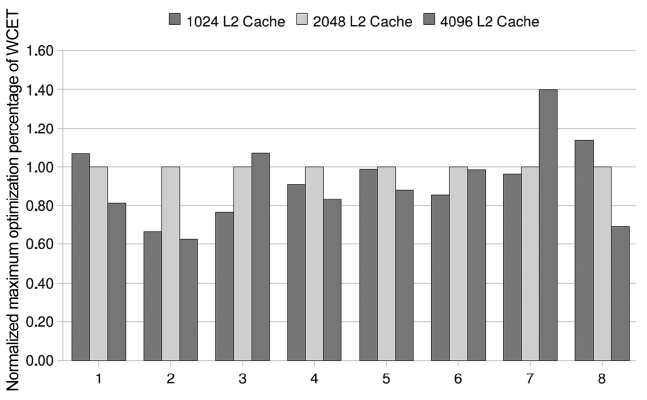
For the WCO scheme, there are three cases in the per-formance optimization variation of the worst-case WCET with an increase of the L2 cache size as shown in Fig. 3. For some benchmark pairs, the optimization percentage of the worst-case WCET by WCO code positioning increases with a larger size of L2 cache. For example, the worst-case WCET of benchmark pair 3 is improved by 8.05% when the cache size is 1,024 bytes. When the L2 cache size is increased to 2,048 bytes and 4,096 bytes, its WCET is reduced by 10.5% and 11.25%, respectively. This is due to the inter-thread L2 conflicts that are avoided by code positioning take a larger portion of the worst-case WCET with larger L2 caches for these bench-mark pairs. However, the optimization percentage decreases when the L2 cache size increases from 1,024 to 2,048, and 4,096 bytes in some benchmark pairs, such as bench-mark pair 1 and 8, as the proportion of the inter-thread L2 misses contained by the worst-case WCET is reduced when the L2 cache size increases. Another case is not quite straightforward and the optimization percentage of
the worst-case WCET increases when the L2 cache size increases from 1,024 bytes to 2,048 bytes. However, it decreases with the L2 cache which increases from 2,048 bytes to 4,096 bytes. The result of benchmark pair 4 is an instance of this case. In this case, there is more free mem-ory space to position the conflicting instructions in order to avoid more inter-thread L2 cache misses when the L2 cache size increases from 1,024 bytes to 2,048 bytes. Thus, the portion of the worst-case WCET taken by the inter-thread cache misses are eliminated by code posi-tioning will increase. On the other hand, when the L2 cache size increases from 2,048 bytes to 4,096 bytes, the number of inter-thread L2 cache misses is reduced and thus it takes a smaller fraction of the WCET. Even if all the inter-thread cache misses can be avoided by code positioning, the optimization percentage induced by them is still less than that in the case of 2,048 byte L2 cache. This is the reason for the decrease in the optimization percentage of the worst-case WCET while the L2 cache size increases from 2,048 bytes to 4,096 bytes.
As illustrated in Table 4, the average difference of the reduced WCET of all the eight benchmark pairs in AFO scheme ranges from 70.5 to 42.5 to 55.75 and the L2 cache size increases from 1,024 bytes to 2,048 bytes to 4,096 bytes. The result of each benchmark pair does not very greatly between the difference changing and the L2 cache size. Therefore, the difference of the reduced WCET is not sensitive to the L2 cache size when it achieves fair-ness on the amount of reduced WCET by the AFO code positioning.
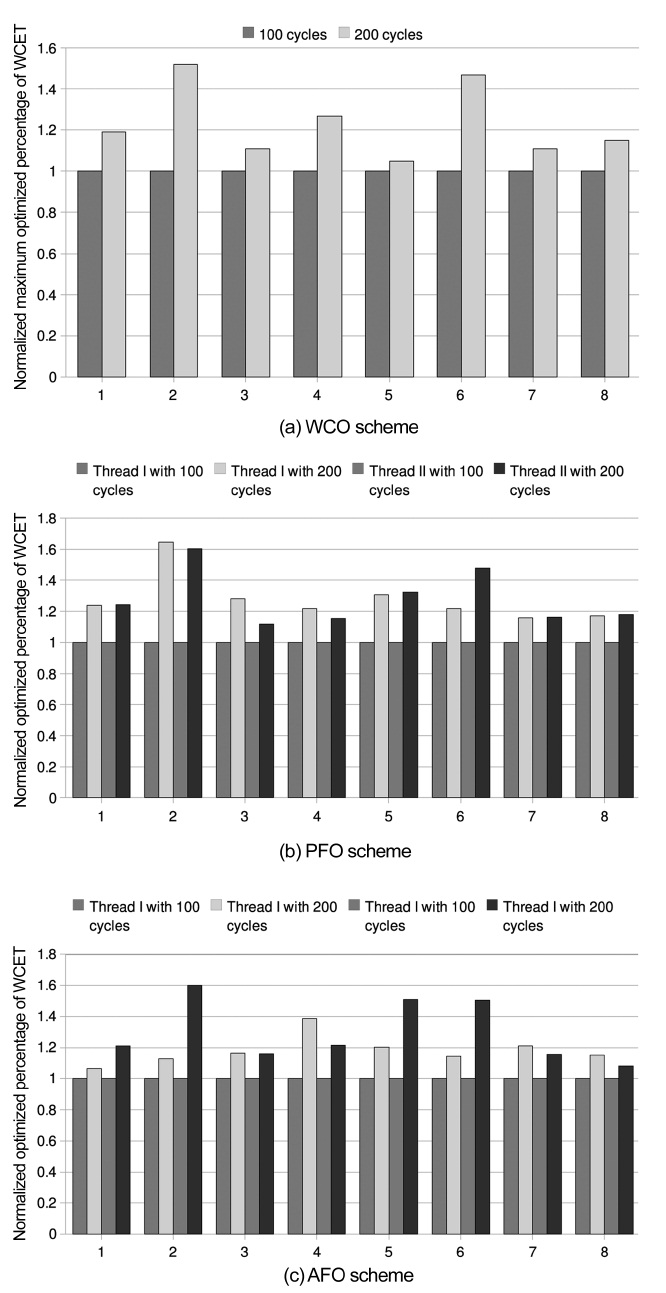
We have studied sensitivity with the memory latency that is increased from 100 cycles to 200 cycles. Under this configuration, the L2 cache miss penalty for a bench-mark obviously takes a larger part of its WCET. By fur-ther deduction, it can be derived that the inter-thread L2 cache conflicts avoided by our co-optimization approach are responsible for a larger portion of the WCET. There-fore, the effect of optimization in this case is better than
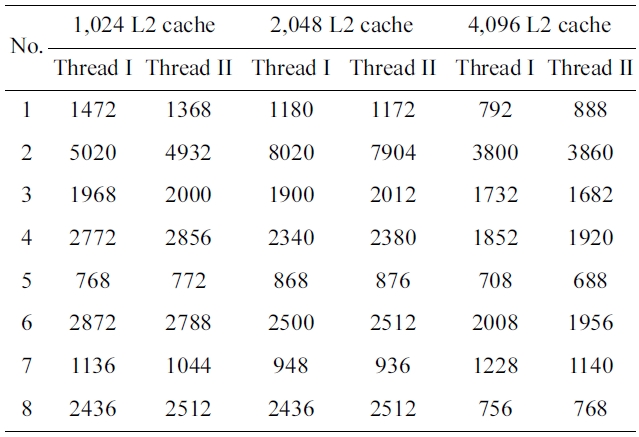
Reduced worst-case execution time of amount-fairness-oriented scheme with respect to baseline scheme with L2 cache size ranging from 1024 bytes to 2048 bytes and 4096 bytes.
that of the basic configuration. This derivation has to be proved by the experiment result that is shown in Fig. 4. For WCO scheme, the average optimization percentage of the WCET of the worst-case thread reaches 9.94% while this data in the basic configuration with 100 cycles of memory latency is only 8.41% as depicted in Fig. 3. And, the WCET optimization percentages of all the benchmark pairs in PFO Scheme with 200 cycles of memory latency are higher when compared to that
obtained in the basic configuration as shown in Table 3. As an example, WCET optimization percentages of the benchmarks in benchmark pair 4 are 9.01% and 8.02%, respectively, and they are larger than 7.40% and 6.94% that was obtained in the basic configuration. Moreover, in case of an AFO Scheme, the average optimized percent-age of WCET with 200 cycles of memory latency is about 18% higher when normalized with respect to the results with 100 cycle memory latency for Thread
>
E. Comparison of Code Positioning Schemes with Separated L2 Caches
In order to compare the performance of the proposed code positioning schemes with the technique of cache partitioning, in our experiments, the 2,048 bytes L2 cache is separated by half. Moreover, only one thread can access one of them to simulate a simple hardware-based cache partitioning (i.e. a separated L2 cache architec-ture). In this paper, it is also called as the SC scheme. As shown in Fig. 5a, for all benchmark pairs the WCETs of both or at least one of the WCO and AFO schemes are better than that of the SC scheme. Even in some of the benchmarks, the performance of the SC scheme is worse than that of the baseline scheme, for instance Cover and Qsort. This is due to the cache partitioning which helps to reduce cache interferences between the different threads and it may bring much more intra-thread cache conflicts as the actual cache mapping space is reduced by half. This is especially problematic if the code size of the working set exceeds the cache size, which is very likely in embedded processors due to the resource constraints. Therefore, for the benchmarks evaluated in this paper, we believe that the code positioning approaches that were studied in this paper are more effective than simply sepa-rating the L2 cache by half in improving the worst-case execution time for real-time tasks.
Current studies on real-time software on multicore pro-cessors are mainly focused on methods to accurately esti-mate the WCET. With the available WCET information, it is also desirable to optimize (or to reduce) WCET on multicore platforms by exploiting compiler transforma-tions. This paper studies the novel compilation time code co-positioning approaches on multicore platforms in order to co-optimize the worst-case performance for real-time threads that run concurrently on a multicore processor with a shared L2 cache. We have studied three different multicore-aware code position schemes to either maxi-mally reduce the longest WCET or to ensure fairness of WCET enhancement among all the co-running threads that can be automatically performed during the compila-tion time.
Our experiments indicate that the WCO scheme can efficiently reduce the worst-case execution time for a sin-gle thread with the worst WCET. It also indicates that the AFO and PFO schemes can reduce the WCETs of co-run-ning threads by approximately the same amount or per-centage, respectively. The evaluation also shows that the multicore-aware code positioning approaches are gener-ally more effective than simply separating the L2 cache by half in order to reduce the worst-case execution time. Moreover, our study indicates that the proposed multi-core-aware code co-positioning approach is even more effective for processors with longer memory access latency. This is likely to be true for future multicore/manycore processors due to the memory wall problem. However, the effectiveness of the three optimization strategies on different L2 cache sizes is largely dependent on the behavior of the concurrent real-time threads.
In our future work, we plan to investigate the interac-tions between inter-thread code positioning which is stud-ied in this paper and intra-thread code positioning such as the work in [3] in terms of improving the worst-case per-formance and to possibly combine them in an efficient manner to achieve even better worst-case performance for real-time application. Moreover, this work is also built upon the inter-thread L2 instruction cache analysis technique in [17] but the multicore-aware code position-ing approach is independent of a specific timing analysis technique. So we plan to examine the use of other multi-core timing analysis techniques in order to further improve the effectiveness of WCET-oriented optimizations. More-over, it will also be interesting to study the multicore-aware data layout optimizations, in addition to code posi-tioning that was studied in this paper, for the attainment of better WCET for real-time tasks that run on multicore processors.





![Worst-case execution time (WCET) and L2 cache miss rate of the worst-case-oriented (WCO) scheme the amount-fairness-oriented (AFO) scheme (which is better than percentage-fairness-oriented [PFO]) and the separated L2 cache (SC) scheme which are normalized with respect to the baseline scheme.](http://oak.go.kr/repository/journal/11651/E1EIKI_2012_v6n1_12_f005.jpg)