Distance information extraction has been the subject of research for numerous applications [1-3]. For depth information to be extracted, three-dimensional (3D) information needs to be acquired and processed. For example, stereo images or a sequence of images are often matched to each other to extract depth information based on pixel disparity [2, 3].

Integral imaging (II) is primarily a 3D display technique but it has been widely adopted for information processing such as obtaining depth information and object recognition [4-11]. During II recording, an elemental image array is generated, that has different views of the object. One advantage of II is that only a single exposure is required to obtain 3D information; no calibration is needed, unlike stereo imaging, and no active illumination is needed, unlike holography or light detection and ranging (LIDAR) [12, 13]. A depth extraction technique using elemental images has been studied in [8-11]. Depth is extracted by means of one-dimensional elemental image modification and a correlation-based multi-baseline stereo algorithm [10]. In [11], the depth level of the reconstruction plan is estimated by minimizing the sum of the standard deviations of the corresponding pixels’ intensity.

Photon-counting imaging has been developed for low-light-level imaging applications such as night vision, and laser radar, radiological, and stellar imaging [14-18]. Advanced photon-counting imaging technology can register a single photo-event at each pixel. In that case, photo-detection is carried out in the binary mode generating a binary dotted image. The object recognition with nonlinear matched filtering is proposed in [19]. II reconstruction with maximum likelihood estimation (MLE) is proposed in [20]. Stereoscopic photon-counting sensing has been proposed for distance infor-mation extraction [21].

This paper proposes the use of photon-counting passive sensing combined with integral imaging for distance infor-mation extraction under low-light-level conditions. Photon-limited imagery is reconstructed with maximum likelihood estimation (MLE). In this paper, the MLE for photon-limited scene reconstruction in 3D space is proposed with the Poisson distribution in [20], while the probability model is modified according to the low-light-level conditions. It has been shown that the MLE is merely the average of the photo-events in the elemental image array. Those photo-events are associated with pixels corresponding to a specific point in 3D space. The obtained depth level is the distance that minimizes the sum of the standard deviations of the corresponding photo-counts. The sum of the standard deviations represents the uncertainty of the sampled information. There have been efforts to minimize the uncertainty in order to reconstruct the occluded scene in [1] and the intensity elemental image array in [11].

Photon-limited elemental images are simulated on a computer while varying the expected total number of photo-events. The performance is evaluated accordingly. We also compare the distance extraction between photon-limited and intensity elemental images. The uncertainty minimization has been applied to both photo-event and intensity cases and consistent results are obtained from both cases. The experimental results confirm that the proposed method can extract distance information under low-light-level conditions. To the best of the authors’ knowledge, it is the first report on distance extraction by use of photon-counting passive sensing combined with integral imaging.

The rest of the paper is organized as follows. Section 2 describes the photo-event model and the distance information extraction algorithm. The experimental and simulation results are presented in Section 3. Conclusion follows in Section 4.

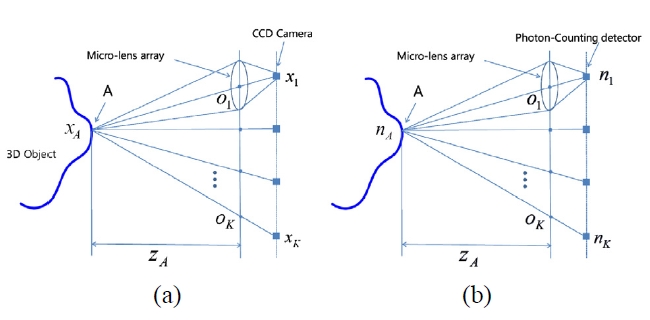
The II recording system generates an elemental image array as illustrated in Fig. 1. The microlens array is composed of a large number of small convex lenslets, and the ray information captured by each lenslet appears as an elemental image, that has different view of the object.

Under low-light-level conditions, a photo-detector can register a single photo-event and generate a binary dotted elemental image array. It can be assumed that the probability of a photo-event is proportional to the intensity of the pixel at a low-light level [15]. Thus, the following probability model is valid:

where y_i indicates a single photo-event at pixel i, N_p is an expected total photo-counts in the scene, x_i is the normali-zed intensity at pixel i, i.e.,

where N_t is the total number of pixels in the scene. It can be seen that E(y_i) = n_i and

Let y_i, where i = 1, 2,… ,K, is the number of photocounts detected at pixel i, which corresponds to the x_i; K is the number of lenslets, which captures the point A in Fig. 1. The joint probability distribution of y_i,… ,y_K, since they are independently registered, becomes

It can be assumed that all n_i’s are equal and proportional to intensity n_A at the point A in the reconstruction plane as illustrated in Fig. 1(b), thus Eq. (3) simplifies to

The MLE (maximum likelihood estimation) of n_A in Eq. (4) is obtained as

which is the average of the photo-counts originated from the point A.

The sum of the standard deviation of the photo-counts over the reconstruction plane is chosen for our metric. It is assumed that the distance level minimizes the sum of standard deviations of the corresponding photo-counts. Therefore, the depth z to the reconstruction plane is estimated as

where N_r is the number of voxels in the reconstruction plane, K_j is the number of the lenslets capturing the voxel j, and y_j,i is the photo-counts in the imaging plane associated with the voxel _j.

Eqs. (6) and (8) are equivalent with Eqs. (9) and (11), which extract distance information in the conventional intensity elemental images as the following [11]:

In the next section, we evaluate the performance of the depth extraction using Eq. (6) with different expected total number of photo-events. The distance extraction derived by intensity images in Eq. (9) is also compared with the photon-limited images.

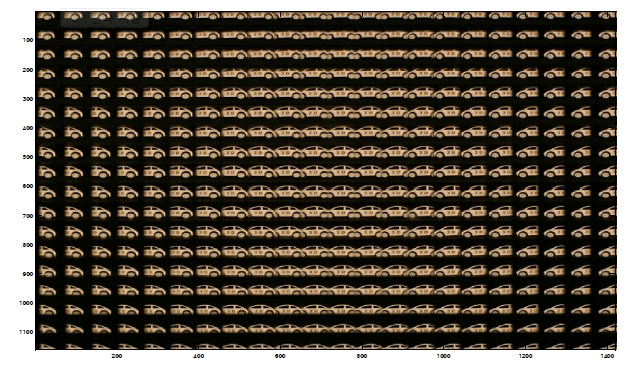
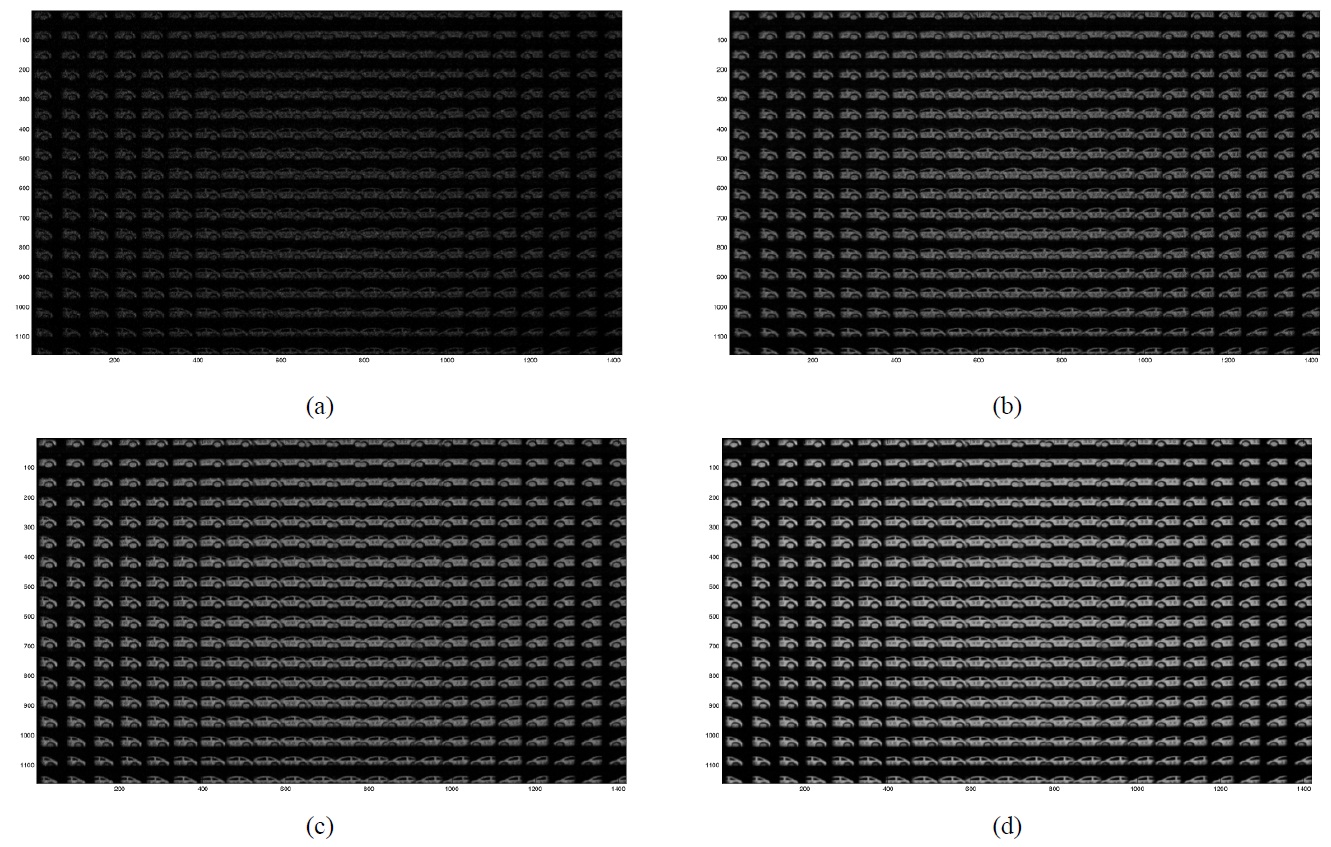
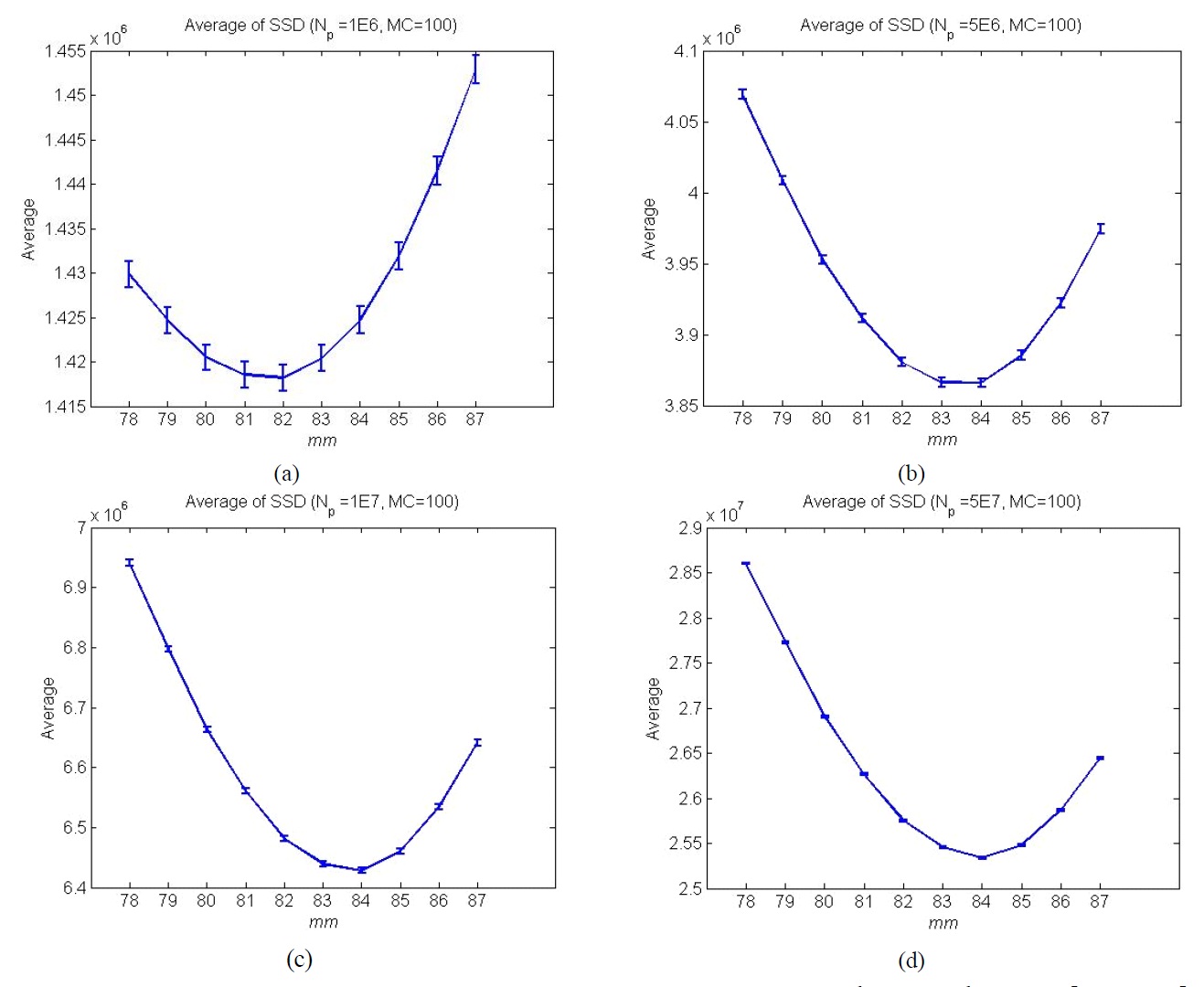
The II recording system is composed of a microlens array and a pick-up camera. The pitch of each lenslet is 1.09 mm, and the focal length of each lenslet is about 3.3 mm. One toy car is used in the experiments. Figure 2 shows the elemental image array. The size of the elemental image array is 1419×1161 pixels and the number of elemental images is 22×18. One-hundred photon-limited elemental image arrays are generated using a pseudo random number generator on a computer. Figures 3(a)-(d) show the examples of the photon-limited images while varying photo-counts; N_p varies as 1 × 10⁶, 5 × 10⁶, 1 × 10⁷, and 5 × 10⁷.

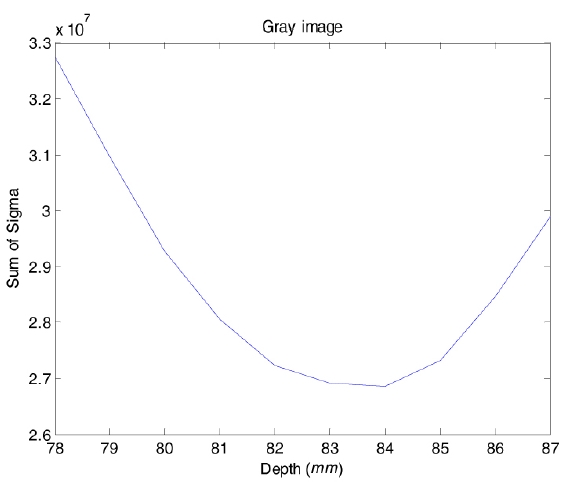
Figures 4 is a plot of the sum of the standard deviations obtained from a gray-scaled image according to Eq. (9) [11]. The sum of the standard deviations is minimized at the depth level of 84 mm. 5(a)-(d) display the average and the error-bar of the standard deviations’sum

over 100 photon limited images, which are obtained by Eq. (6). As more photo-events are acquired, the photon-limited image starts to resemble the intensity image in Fig.3, and the results in Fig. 5 approach those of Fig. 4. In this experiment, the depth level can be extracted when the photo-counts exceed 5×10⁶ as illustrated in Fig. 5(b).

In this paper, a photon-counting integral imaging method for distance information extraction is proposed. The depth level of the object is determined by the distance at which the sum of the standard deviations of the photo-counts is minimized. The method is based on a compact system that requires only a single exposure under passive mode to obtain 3D information. Experimental and simulation results confirm that the proposed method can be used to obtain the distance information to an object at a low-light level. It was confirmed that the depth level is the same as the intensity images. Further investigation on the distance infor-mation extraction of multiple or occluded objects under low-light-level conditions remains for future study.