Three-dimensional (3D) holographic imaging systems [1-10] have been investigated for achieving reliable and non-invasive recognition and for identifying biological micro /nano organisms [11-14]. The 3D holographic imaging system for biological microorganism analysis has a large number of biological applications such as medical diagnosis, medical therapeutics, bio-medical imaging, defense, and security.
Red blood cells (RBCs) have been extensively studied for bio-medical applications. Recent studies on RBCs have suggested that transfusions of blood having long storage periods or abnormal shapes increase risk after transfusion [15,16] since long storage and abnormal shapes progressively change the RBCs’ structure and function, which may reduce RBC function and viability [15]. Consequently, the development of free labelling techniques that allow rapid classification of older versus newer red blood cells is very useful. In general, most traditional methods of studying biological cells such as RBC require biochemical processing, which may be time-consuming and labor- intensive. Furthermore, the recognition techniques based on two-dimensional imaging may not be effective because RBCs are usually semitransparent. Thus, the automatic 3D classification of RBCs can be very useful. Otherwise, the RBCs would be investigated in very low contrast or invisible under conventional microscopy.
Recently developed techniques in 3D holographic microscopy have provided a high resolution and noninvasive examination to identify biological cells [11-14]. In this paper, we propose an automated algorithm to quantitatively measure a 3D volume of RBC using digital holographic microscopy for the purpose of identifying various types of RBCs. The proposed technique for quantitative analysis of a 3D volume of RBCs includes 3D sensing, visualization, segmentation, and statistical methods. Off-axis digital holographic microscopy [17-20] is applied to three-dimensionally sense the RBCs [14]. Their original phase images are restored by using special numerical algorithms. As part of pre-processing RBCs 3D volume analysis, it is important to remove the background parts and select regions of interest in the restored RBCs’ phase image [14]. Here, the watershed segmentation algorithm [21] is applied to the reconstructed phase image to obtain clear targets in the phase image with many single RBCs. After segmenting the reconstructed RBC’ s phase image, all single RBCs are extracted and the 3D volume of each single RBC is then measured via the surface area and the phase values of the corresponding RBC. In order to show the feasibility of the proposed method, two typical shapes of RBCs, i.e.,
II. AUTOMATIC PROCEDURES FOR RBCs 3D VOLUME MEASUREMENT
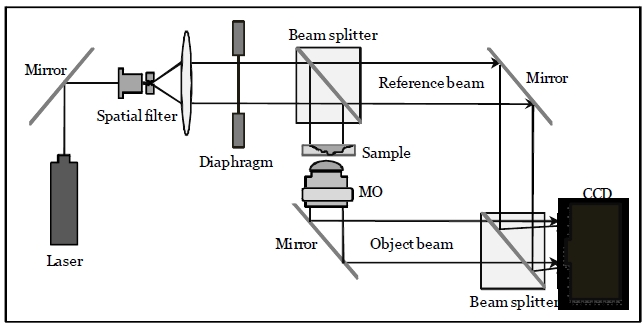
The off-axis digital holographic imaging system [24,25] is employed for 3D sensing of RBCs, which has been described in [20]. As shown in Fig. 1, the off-axis digital holograms of RBCs are acquired via a CCD camera. In this configuration, a laser beam with a wavelength of 682 nm is divided into reference and object beams. The object beam is diffracted by the RBC specimens. A 40× / 0.75NA microscope objective (MO) magnifies the diffracted object beam. The interference patterns between the diffracted object
and reference beams in the off-axis geometry are recorded by the CCD camera. The numerical algorithms described in [17,18] reconstruct the RBCs’ wavefront or phase image from the off-axis digital hologram.
In order to measure the RBC’ s 3D volume in the reconstructed phase image, the watershed segmentation algorithm [21] is applied to the phase image in order to remove background parts and obtain clear targets in the phase image with many single RBCs [14]. Every single RBC in the phase image is extracted individually. Then, the projected surface area and phase values are automatically calculated for every single RBC, which are utilized to calculate the 3D volumes of the corresponding RBCs. The 3D volume measurement for a single RBC, which is related with its 3D shape, can be given by:
where
In our experiments, the off-axis digital holograms of two different shapes of RBCs [class 1: RBCs with a
Since most single RBCs appear to have two kinds of
regions as shown in Fig. 4, it is better to respectively separate the different parts to achieve a comprehensive and detailed analysis of the RBCs 3D structure. Here, different regions of RBCs are defined in Fig. 4. The C region includes A and B parts, where the A part apparently has relative lower phase values than those of B part. Most of the A part is on the interior of the RBC, while the B part forms the boundary of the RBC.
In order to obtain the different regions in the RBCs, we first use the marker-controlled watershed algorithm to obtain the C part. Then, the C part is taken as a source
image, and we can obtain the A part by applying the markercontrolled watershed. Finally, the B part can be obtained by subtracting the A part from the C part. Figure 5 shows the segmented phase images of the A and the B parts in the reference and input RBCs, respectively.
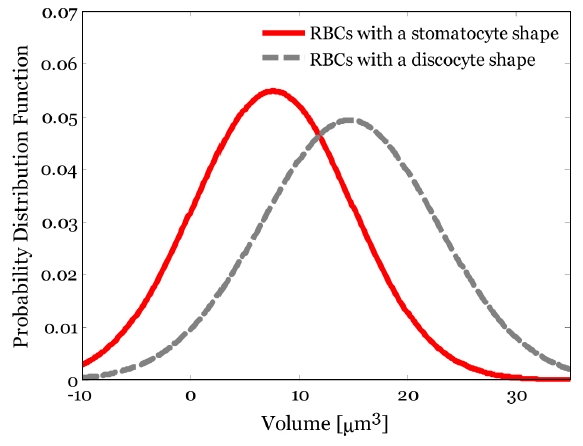
To conduct a quantitative investigation of the 3D volumes of RBCs with two different shapes, the 3D volumes in the A, B, and C parts [see Fig. 4] of single RBC are calculated using Eq. (1), respectively. To conduct a statistical analysis of RBCs volume, the mean and standard deviation of the volume of the A part in RBCs with a
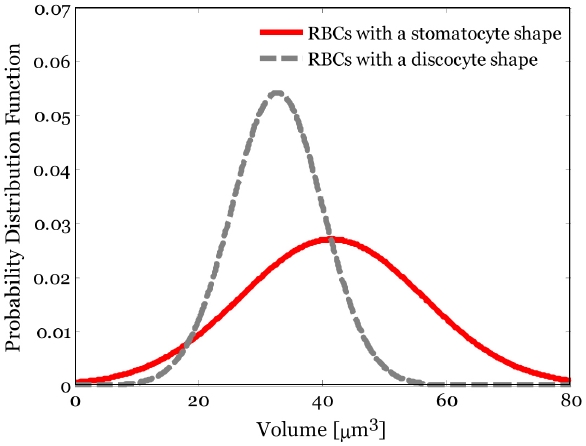
Figure 7 shows the statistical distributions of 3D volume of the B part in the two different shapes of RBCs. The mean and standard deviation of the volume of the B part in RBCs with a
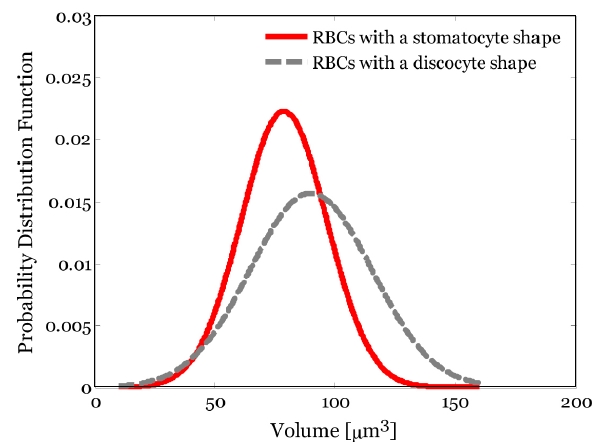
Figure 8 shows the statistical distributions of 3D volume of the C part in the two different shapes of RBCs. The mean and standard deviation of the volume of the C part in RBCs with a
with
In order to statistically evaluate there is a significant 3D volume distinction in RBC populations that differ in shape, we define the 3D volumes in the A, B, and C parts of each single RBC as random variables
In order to compare the dispersion parameters between the two statistical normal distributions [c1: stomatocyte shape, c2: discocyte shape], it is assumed that all four statistical parameters are unknown and
where the
To answer and discuss this important question on whether or not there is a distinction in 3D volume of A, B, or C part between the two different shapes of RBCs [c1:
The difference of location parameters of the two independent normal populations for the null hypothesis [
where the variable
[
[
The statistical decision analysis on the equality of the location parameter between the statistical distributions of the two different shapes of RBCs for each random variable
These statistical experiments demonstrate that there is a considerable distinction between the RBCs 3D volumes and their shapes. Accordingly, we believe that the proposed method has potential for achieving statistical quantifications of the 3D volume in various types of RBCs. In addition, it can be a promising tool for investigating any modifications or dynamics of 3D volume in RBC by monitoring RBCs.
In this paper, we have proposed an automated method for 3D volume measurement of red blood cells (RBCs) using off-axis digital holographic microscopy. The off-axis digital holographic microscopy has recorded hologram patterns of RBCs. The RBCs phase images have been reconstructed from their holograms by using special numerical algorithms. Segmentation algorithms have been applied to the RBCs phase image in order to remove the unnecessary background and obtain clear targets in the reconstructed phase image. The 3D volumes of every single RBC in the segmented phase image have been calculated. Statistical hypothesis testing has been conducted in order to investigate whether or not there is a significant difference between the statistical distributions of the 3D volume of two different shapes of RBCs, i.e.,
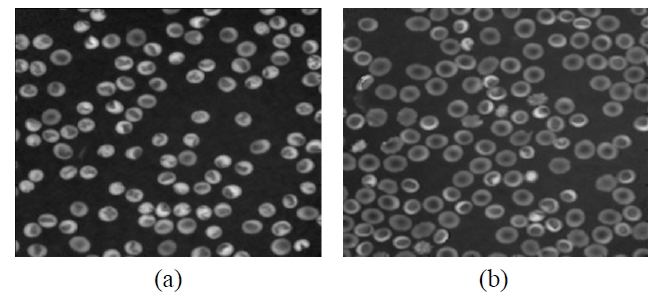
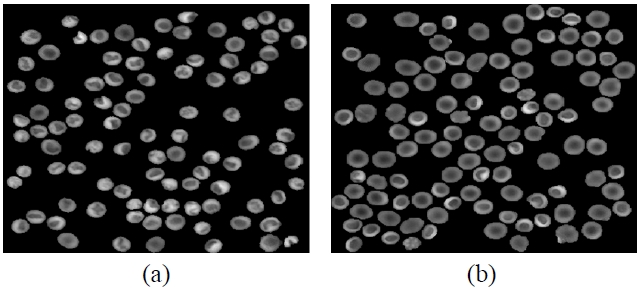

![The segmented phase images of the A and B regions [see Fig. 4] in the RBCs. (a) Segmented phase image of the A part in the class 1 RBCs having a a stomatocyte shape. (b) Segmented phase image of the A part in the class 2 RBCs having a discocyte shape. (c) Segmented phase image of the B part in the class 1 RBCs having a stomatocyte shape. (d) Segmented phase image of the B part in the class 2 RBCs having a discocyte shape.](http://oak.go.kr/repository/journal/11476/E1OSAB_2012_v16n2_115_f005.jpg)