Langasite (La3Ga5SiO14 (LGS)) is piezoelectric crystal named according to its composition, that is, La, Ga and Silicate mineral is named langasite with "ite" as the ending of a mineral name. Over one hundred langasite group compounds have been found with the structural formula
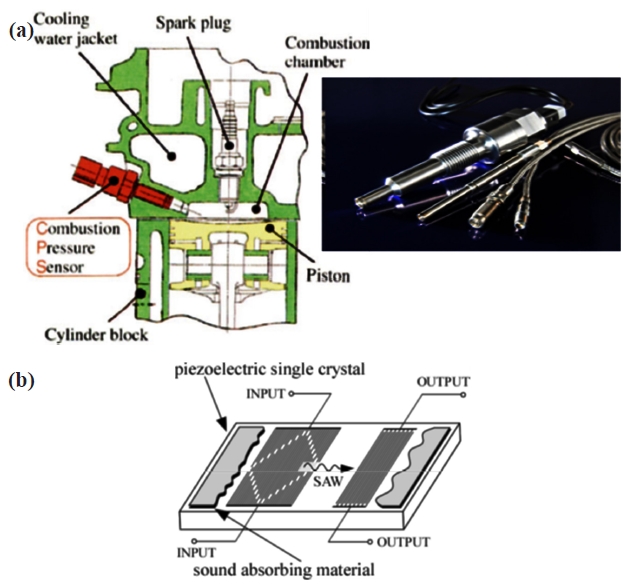
The special characteristic of langasite is high temperature performance based on its lack of Curie point and lack of phase transition until melting point around 1500℃, and a lack of pyroelectricity, depending on whether or not the point group 32 is the same as quartz, which will be described later. The application for high temperature has been used for combustion (burning) pressure sensors in combusting engines as shown in Fig. 1(a) [9]. And, as the piezoelectric constant and the pass band filter characteristics are about 3 times that of quartz crystal, and because of near-zero
Moreover, langasite crystals have good points for single crystal growth. Single crystals are easily grown because of a low temperature melting point of about 1500℃ allowed use of Pt-crucible, none-phase transition, and congruent melting. And many kinds of methods can be used for crystal growth.
In this review paper, crystal growth, crystal structure, the properties, the mechanism of piezoelectricity, and the crystal structure under high pressure are presented.
2. CRYSTAL GROWTH OF LANGASITE
Langasite group single crystals have been grown by many growing methods such as Czochralski (Cz) technique, Bridgeman method, floating zone (FZ) method, and micro-pulling down (μ-PD) technique, as these crystals grow easily [10-12].
LGS, Pr3Ga5SiO14 (PGS) and Nd3Ga5SiO14 (NGS) single crystals shown in this chapter were grown by a conventional radiation frequency (RF)-heating Cz-method with an output power of 60kW by Sato
Defect-free LGS, PGS and NGS single crystals with constant diameter of 22 mm and lengths up to 145 mm were grown as shown in Figs. 2(a), (b) and (c), respectively [12]. These ingot diameters were highly consistent over the whole length. The optimum pulling rates are lower than 1.5 mm/h for inclusion-free perfect single crystals, and a higher temperature gradient at the growing interface controls the growth, preventing distinct facet enlargement and asymmetrical growth leading to spiral morphology.
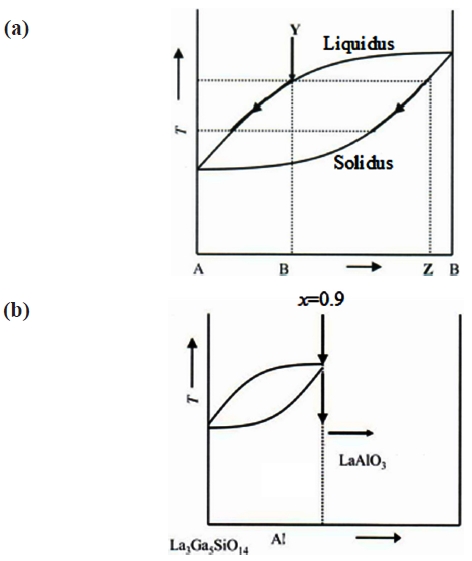
LGS compounds with congruent melting are grown easily because of the same composition of growth crystals and liquid. In the case of solid solutions, the composition of the precipitated crystal gradually changes during crystal growth as shown in Fig. 3(a). Takeda & Tsurumi [13] presented crystal growth with homogeneous composition from quasi-congruent melt [14,15]. In the case of Al-substituted La3Ga5-xAlxSiO14 (LGASx), as the limitation of the solid solutions is located at
are grown as quasi-congruent melt growth.
3. CRYSTAL STRUCTURE OF LANGASITE
Langasite crystal structure was analyzed originally by Mill
The crystal structure figures projected from [001] and [120] are shown in Fig. 4(a) and 4(b), respectively. The structure represented by the structural formula,
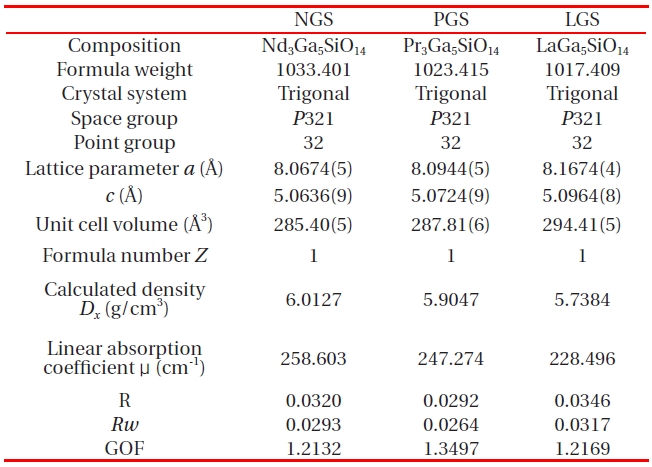
[Table 1.] Crystallographic data of NGS, PGS and LGS.
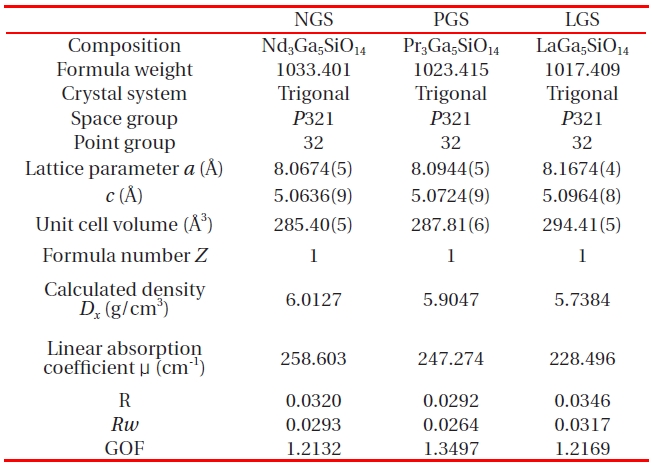
Crystallographic data of NGS, PGS and LGS.
half of the
The crystal structures among LGS, PGS and NGS differ mostly in the shape of each site. In particular, the change of the
4. PIEZOELECTRIC PROPERITES OF LANGASITE
4.1 Electric properties based on point group
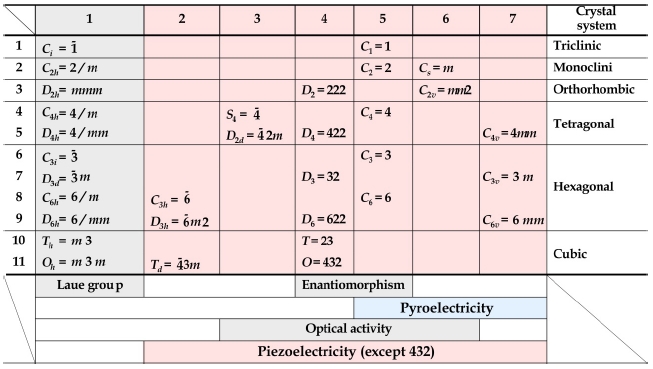
The point group of langasite is 32, which is the same as quartz,
[Table 2.] Point group and properties.
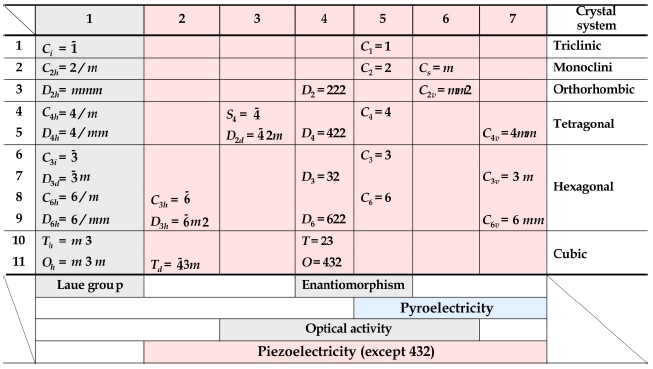
Point group and properties.
and has no inversion symmetry
4.2 Polarity direction by point group
As langasite is a non-polar piezoelectric crystal, poling treatment is not necessary. However ceramics that are polycrystals show isotropic properties as a whole because each orientation of grains can turn to any direction. So, non-polar piezoelectric materials should be used as a single crystal. For a single crystal, the knowledge of the directions of piezoelectricity is very important. As the directions are the same as for polar, they could be derived based on the point group.
Figure 5 shows the stereographic projection of general positions in the point group. Figure 5(a) shows the [001] direction without polarity because of the same number of ○ and × positions on the opposite sides of [001]. The [210] direction (Fig. 5(c)) is also non-polar by the same manner. Only the [100] direction shows polarity as shown in Fig. 5(b). The configurations of a typical crystal of the point group 32 are shown along the stereographic projections, with crystal surfaces plotted on the stereo projections. The crystal structures along [120] and [100] as shown in Fig. 5(d) and (e) show asymmetry and symmetry, respectively, along the left and right directions. Now, Fig. 6 shows a
4.3 Piezoelectric properties of langasite
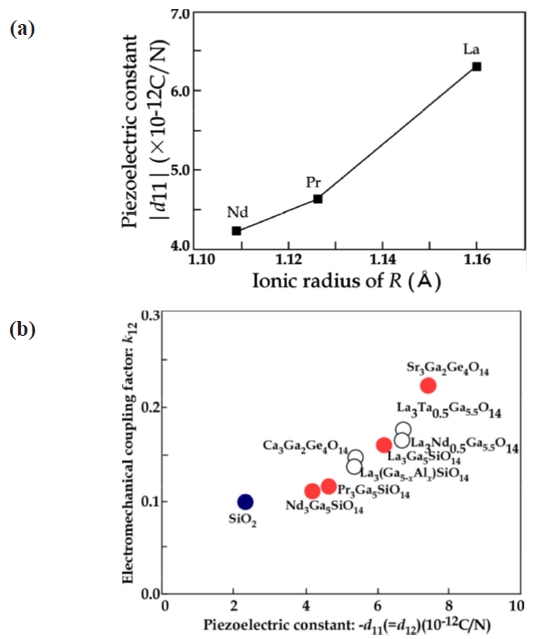
Piezoelectric strain constants
the
On the other hand, Sr3Ga2Ge4O14 with Sr in the
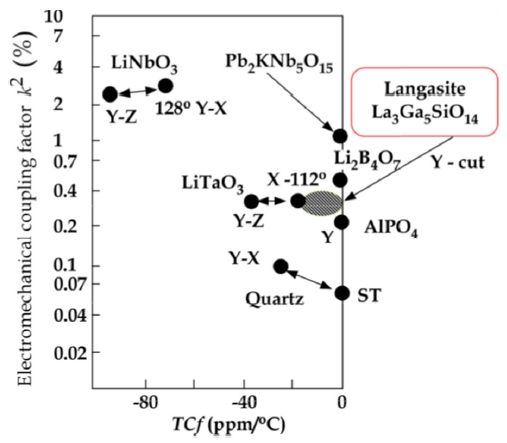
Figure 9 shows the electromechanical coupling factor
tion system. Langasite has been expected for use as a SAW filter to replace quartz and LiTaO3 because of its wide bandwidth and near-zero
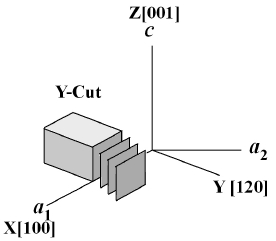
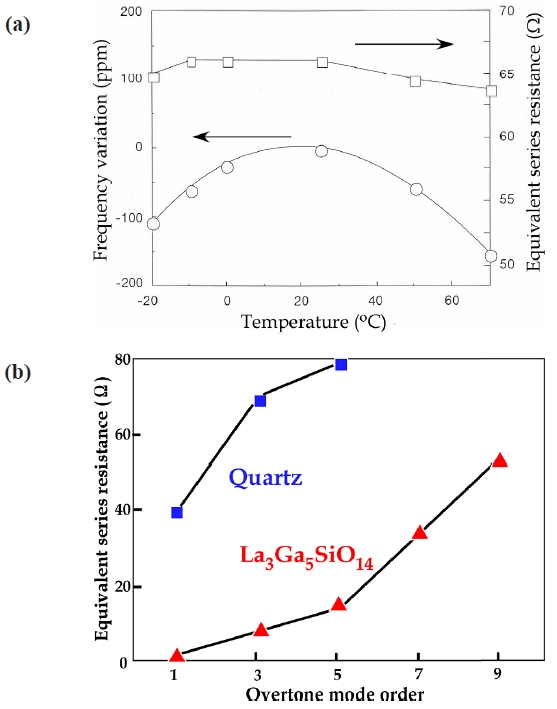
Figure 10(a) shows the temperature dependence of frequency and the equivalent series resistance of a filter made of Y-cut LGS single crystal [11]. The temperature dependence of frequency shows a secondary curve with good values of 1-2 ppm/℃. In the range of -20 to 70℃, the dependence of temperature shows good values of 100 to 150 ppm/℃. Figure 10(b) shows the equivalent series resistance as a function of vibration modes of resonators on the LGS and quartz single crystals [11]. The resistance of
LGS is one order smaller than that of quartz. So, as if the surface roughness of LGS is large, high frequency oscillation is easy. Moreover, as the equivalent series resistances at the 7th and 9th modes are small, the LGS filter is useful as a high frequency wave area filter.
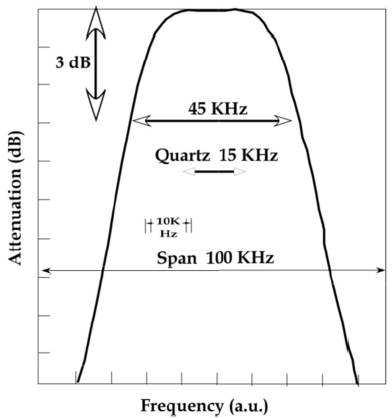
Figure 11 shows pass band characteristic of a filter made of Ycut LGS single crystal [4,11]. Y-cut LGS single crystal has a very wide pass band characteristic width of 45 KHz at 3 dB attenuation,which is 3-times that of quartz with 15 KHz band width.This means the electromechanical coupling constant
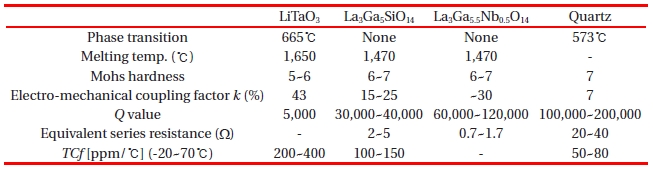
Table 3 shows the properties comparing some piezoelectric crystals such as LiTaO3, LGS, quartz, and La3Ga5.5Nb0.5O14 (LGN) [4]. The properties of LGS are between LiTaO3 and quartz. The electro-mechanical coupling factor k of LGS is 15 to 25%, located
[Table 3.] Comparison of properties of each crystal.
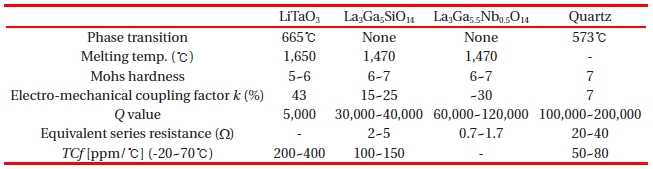
Comparison of properties of each crystal.
between that of LiTaO3 at 43%, and quartz at 7%. The temperature frequency variation of LGS is 100 to 150 ppm/℃, located between that of LiTaO3 at 200 to 400 ppm/℃, and quartz at 50 to 80 ppm/℃. Here, LGN single crystal substituted for Nb5+ and Ga3+ for Si4+ has superior piezoelectric properties.
4.4 Ordered crystal structure and properties
LGS, PGS and NGS are compositionally disordered crystals. The structural formulae are [R3]A[Ga]
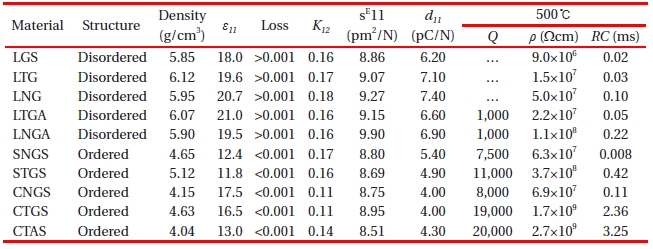
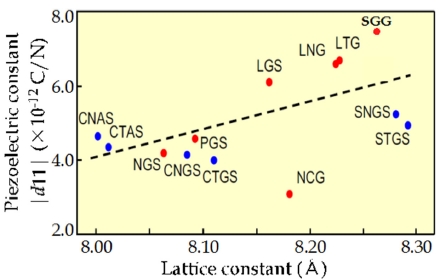
Table 4 shows the characterization of disordered and ordered langasite-type piezoelectric single crystals at room temperature and 500℃ [22]. Though the ordered crystals possess lower piezoelectric coefficients than disordered ones at room temperature as shown in Fig. 12 [23], they possess much higher mechanical quality factor and electrical resistivity at an elevated temperature of 500℃. The high mechanical quality factor and the high electrical resistivity have been expected for use in a hightemperature bulk acoustic wave (BAW) and SAW resonator and ignition pressure sensor, respectively. The density and dielectric constant of ordered crystals are lower than those of disordered ones, which contribute to the high acoustic velocity in high frequency devices. LTGA and LNGA disordered crystals in Table 4 have substituted Al for Ga in La3
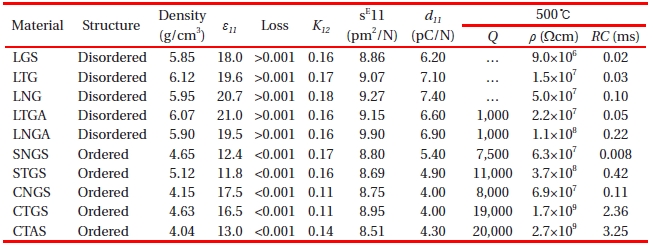
Characterization of disordered and ordered langasitetype piezoelectric single crystals at room temperature and 500℃. LTG:La3Ta0.5Ga5.5O14; LNG:La3Nb5GaO14; LTGA: La3Ta0.5Ga5.3Al0.2O14; LNGA: La3Nb0.5Ga5.3Al0.2O14; SNGS: Sr3NbGa3Si2O14; STGS: Sr3TaGa3Si2O14; CNGS: Ca3NbGa3Si2O14; CTGS: Ca3TaGa3Si2O14; CTAS: Ca3TaAl3Si2O14.
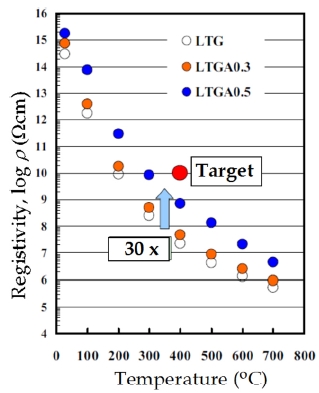
in that order, at 400℃ as shown in Fig. 13 [24]. The resistivity of LTGA0.5 increased to about 30 times that of LTG. Al-substituted LGS (La3Ga5-xAlxSiO14: LGASx) were also studied for high resistivity at elevated temperature and low cost, which was presented by Kumatoriya
5. CRYSTAL STRUCTURE UNDER PRESSURE AND MECHANISM OF PIEZOELECTRICITY OF LANGASITE
5.1 Crystal structure under pressure
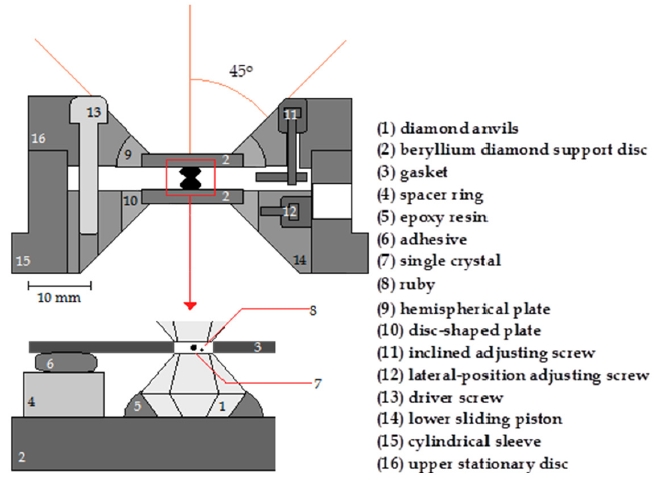
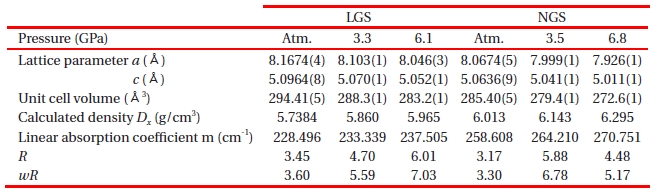
In this section, the mechanism of the piezoelectricity has been presented based on the crystal structure and deformation under applied pressure. Pressures applied to the single crystals using a diamond anvil cell (DAC) as shown in Fig. 14 were calibrated by the ruby fluorescence technique. The DAC was set on the four-circle diffractometer. The unit cell parameters were refined by using the 2Θ-ω step scan technique. Table 5 shows crystallographic data of LGS and NGS including the lattice parameters measured at various pressures.
The pressure dependence of lattice parameters (
[Table 5.] Crystallographic data of LGS and NGS under pressure.
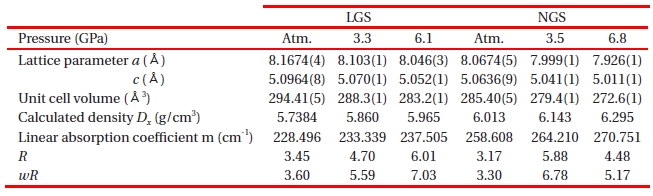
Crystallographic data of LGS and NGS under pressure.
direction of
5.2 Mechanism of piezoelectricity of langasite
Iwataki
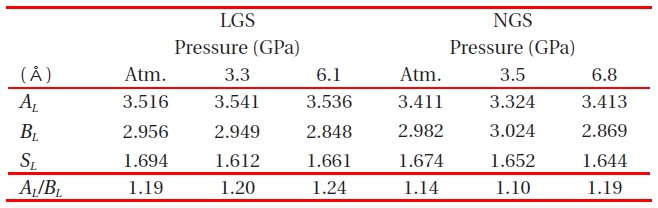
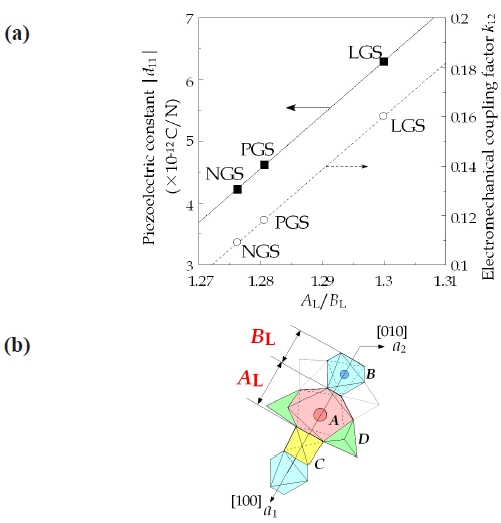
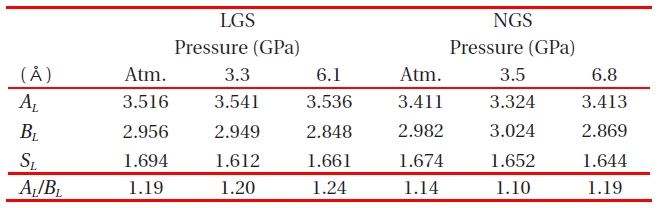
A- and B-polyhedra size AL and BL, and open-space size SL along a-axis and AL/BL for LGS and NGS. Atm.: atmosphere pressure.
of langasite based on the deformation of the
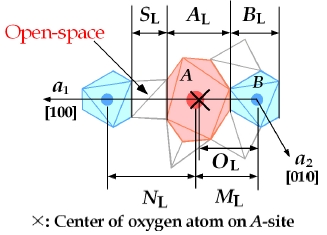
Figure 17. Mechanism of piezoelectricity on langasite projected from [120]. Position X is the center of oxygen atoms on A-polyhedron. Under pressure,
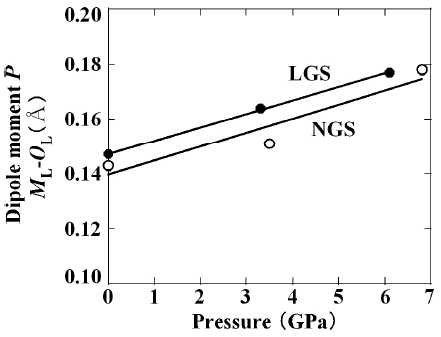
With an induced pressure, the distance
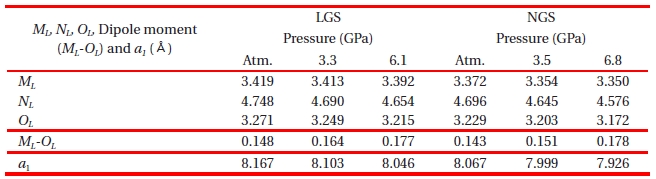
Atomic distances (ML NL) center position X-B ion distance (OL) dipole moment (ML - OL) and lattice constant of a1 of LGS and NGS along [100] direction under the pressure. Atm.: atmosphere pressure.
cations as shown in Fig. 16 and Table 7 is not changed around 3.4 A, and the distances of
The reason for La-langasite having larger piezoelectricity than Nd-langasite is clarified by the difference of the
6. NEW PIEZOELECTRIC MATERIALS WITH FRAMEWORK CRYSTAL STRUCTURE
Langasite is a kind of materials formed a framework structure without inversion symmetry
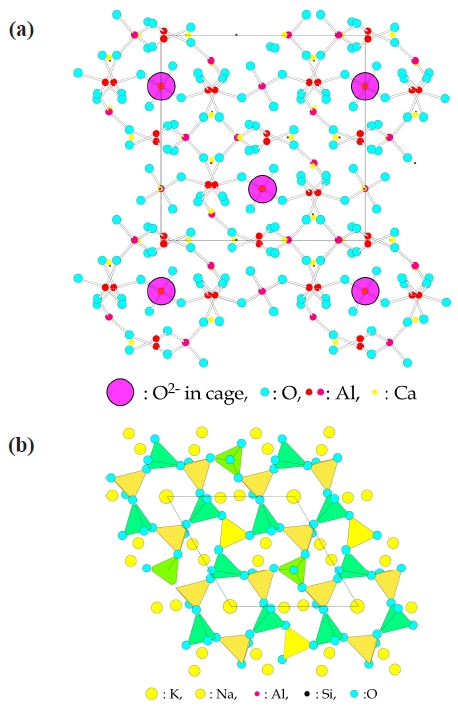
Recently, Hosono [27] presented that Ca12Al14O32 (C12A7) clinker compound with big cages including O2- in a [Ca24Al28O64]4+ framework shows specific properties such as electride, transparent electride, transparent p-type conducting oxides, transparent semiconductor, super conductor, and other properties. The crystal structure has 12 cages of 4.4 A in diameter in a unit cell of a 12 A cube, and 2 cages of those 12 include oxygen ion (O2-) as shown in Fig. 19(a). As this O2- is bonding weakly with the framework, this ion could be removed or exchanged with other anions easily. Transparent metal oxide (C12A7:H-) transformed to electro conductor by photon-induced phase transition, C12A7 compound including much active oxygen O- atoms [28,
Here, we will present a candidate for piezoelectric materials. Nepheline (KNa3Al4Si4O16) is one of the alumino-silicates with framework as shown in Fig. 19(b). The crystal structure has a hexagonal ring framework without i based on the space group
This review paper is presented about the crystal structure and mechanism of piezoelectricity of langasite. The mechanism of piezoelectricity was derived based on the crystal structure and deformation of crystal structure under high pressure. Openspace in the langasite framework structure plays a key role in the mechanism of piezoelectricity. So, the framework structure should be noticed from the point of view of the piezoelectricity. And general knowledge for properties is presented based on the point groups which are applied for derivation of the piezoelectricity direction. Moreover, there are two important aspects for applications of langasite: one is the easy crystal growth based on a low melting point of 1,470℃ resulting in no phase transition and congruent melting; another is the high performance piezoelectricity properties such as high temperature performance based on the lack of phase transition and better piezoelectric properties compared to quartz. This reviewed paper is written based on "Origin of Piezoelectricity on Langasite"

![Crystal structure of Langasite. (a) a1-a2 plane and (b) a1-c plane are viewed from [001] and [120], respectively. (c) four kinds of cation of cation polyhedra. is four kinds of cation polyhedra.](http://oak.go.kr/repository/journal/11419/E1TEAO_2012_v13n2_51_f004.jpg)
![Determination of piezoelectricity direction based on point group 32. Stereo graphs (a), (b) and (c) with equivalent points are projected from [001], [100], and [210], respectively. x:upper points, o: opposite points. Configurations of a crystal with point group 32 also are drawn for supporting the stereo projections. (d) and (e) show the crystal structure along [100] and [120] showing asymmetry and symmetry, respectively. Dipole moment will appear in (d).](http://oak.go.kr/repository/journal/11419/E1TEAO_2012_v13n2_51_f005.jpg)
![Atomic distances (ML NL) center position X-B ion distance (OL) dipole moment (ML - OL) and lattice constant of a1 of LGS and NGS along [100] direction under the pressure. Atm.: atmosphere pressure.](http://oak.go.kr/repository/journal/11419/E1TEAO_2012_v13n2_51_t007.jpg)
![Mechanism of piezoelectricity on langasite projected from [120]. Position X is the center of oxygen atoms on A-polyhedron. Under pressure, ML does not change and NL shrinks because of the role of open-space as a damper.](http://oak.go.kr/repository/journal/11419/E1TEAO_2012_v13n2_51_f017.jpg)