Composite materials are being increasingly used in aerospace, civil, naval and other high-performance engineering applications due to their light weight, high specific strength, stiffness, excellent thermal characteristics, and ease in fabrication and other significant attributes. Structures used in the above fields are very often exposed to high temperatures as well as moisture. The varying environmental conditions due to moisture absorption and temperature seem to have an adverse effect on the stiffness and strength of the structural composites. This wide range of practical applications demands a fundamental understanding of their vibrations, static and dynamic stability characteristics under hygrothermal conditions. Thus the parametric resonance characteristics of laminated composite curved panels subjected to hygro-thermoelastic loads are of tremendous practical importance in the prediction of structures behavior under in-plane periodic loads.
The previous studies on vibration and buckling of composite panels subjected to hygrothermal loads are available in literature and reviewed by Tauchert [1] through 1991. The effects of hygrothermal conditions on the free vibration of laminated panels was considered earlier by Whitney and Ashton [2] using the Ritz method based on the classical laminated plate theory. Sai Ram and Sinha [3] and Patel
A geometrically nonlinear analysis of linear viscoelastic laminated composite systems subjected to a mechanical and hygrothermal load was presented by Marques and Creus [9] considering three-dimensional degenerated shell element. The nonlinear free vibration behavior of laminated composite shells subjected to a hygrothermal environment was investigated by Naidu and Sinha [10]. The geometrically non-linear vibrations of linear elastic composite laminated shallow shells under the simultaneous action of thermal fields and mechanical excitations are analysed by Ribeiro and Jansen [11]. The vibration characteristics of pre and postbuckled hygro-thermo-elastic laminated composite doubly curved shells was investigated by Kundu and Han [12]. Panda and Singh [13] studied the nonlinear free vibration behavior of single/doubly curved shell panels which addressed the post-buckled state where thermal post-buckling of shell panels was accounted for in a uniform temperature field. The finite element method was applied to study the problem of moisture and temperature effects on the stability of a general orthotropic cylindrical composite shell panels subjected to axial or in-plane shear loading by Lee and Yen [14]. The effect of hygrothermal conditions on the post buckling of shear deformable laminated cylindrical shells subjected to combined loading of axial compression and external pressure was investigated using a micro-to-macro mechanical analytical model by Shen [15]. Finally, the hygrothermoelastic buckling behaviour of laminated composite shells were numerically simulated using a geometrically nonlinear finite element method was studied by Kundu and Han [16]. The effect of random system properties on the post buckling load of geometrically nonlinear laminated composite cylindrical shell panels subjected to hygro-thermo-mechanical loading is investigated by Lal
The dynamic stability or, more particularly, the phenomenon of parametric resonance in cylindrical shells under periodic loads has attracted much attention due to its detrimental and de-stabilizing effects in many engineering applications. This phenomenon in elastic systems was first studied by Bolotin [18], where the dynamic instability regions were determined by a solution of the Mathieu-Hill equation. Based on Donnell’s shell equations, the dynamic stability of circular cylindrical shells under both static and periodic compressive forces was examined by Nagai and Yamaki [19] using Hsu’s method. Bert and Birman [20] extended the study of the parametric instability of thick orthotropic shells using higher-order theory. Liao and Cheng [21] proposed a finite element model with a 3-D degenerated shell element and a 3-D degenerated curved beam element to investigate the dynamic stability of stiffened isotropic and laminated composites plates and shells subjected to in-plane periodic forces. Argento and Scott [22] employed a perturbation technique to study the dynamic stability of layered anisotropic circular cylindrical shells under axial loading. The study of the parametric instability behavior of curved panels, the effects of curvature and aspect ratio on dynamic instability for a uniformly loaded laminated composite thick cylindrical panel was studied by Ganapathi
However, all the above studies deal with the parametric resonance characteristics of composite shells without considering the hygrothermal effects. To the best of this author’s knowledge, no study has reported on the dynamic instability of laminated composite panels under hygrothermal loads. In the present study, the parametric resonance characteristics of plates/cylindrical/doubly curved composite panels subjected to hygrothermal loading are investigated using the finite element method (FEM). Quantitative results are presented to show the effects of curvature, ply-orientation, and degree of orthotropy and geometry of laminate on parametric instability of composite panels for different temperature and moisture concentrations.
The mathematical formulations for parametric instability behavior of laminated composite panels due to in-plane periodic loading consideration in hygrothermal conditions are presented.
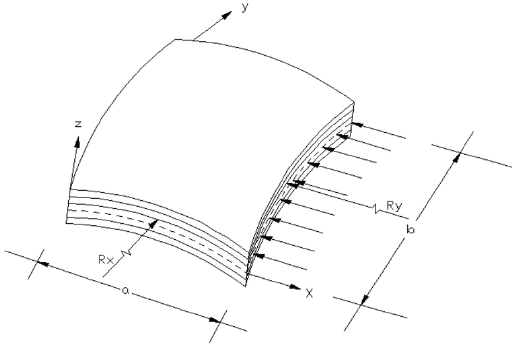
The basic configuration of the problem considered here is a doubly curved panel with in-plane loadings subjected to hygrothermal conditions as shown in Fig.1.
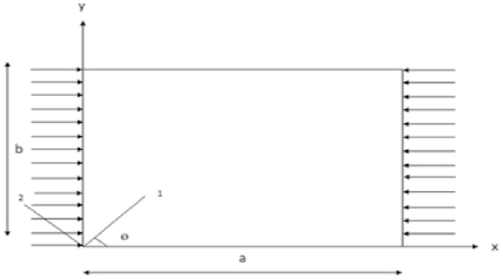
The choice of the doubly curved panel geometry as a basic configuration has been made so that depending on the value of curvature parameter orplate, cylindrical panels and different doubly curved panels can be considered on a case by case basis. Consider a laminated panel of uniform thickness ‘t’, consisting of a number of thin laminate, each of which may be arbitrarily oriented at an angle ‘θ’ with reference to the X-axis of the co-ordinate system as shown in Figures 2 and 3.
The governing equations for the dynamic stability of laminated composite doubly curved panels/shells subjected to hygrothermal loading are developed. The equation of motion represents a system of second order differential equations with periodic coefficients of the Mathieu-Hill type. The development of the regions of instability or dynamic instability regions (DIR) arises from Floquet’s theory and the solution is obtained using Bolotin’s approach using the finite element method (FEM). The governing differential equations have been developed using first order shear deformation theory(FSDT). The analysis is linear and the loading considered is axial with a simple harmonic fluctuation with respect to time. All damping effects are neglected.
The governing differential equations for vibration of a shear deformable composite plates and shells in hygrothermal environments are derived on the basis of first order shear deformation theory subjected to in-plane loads:
Where N
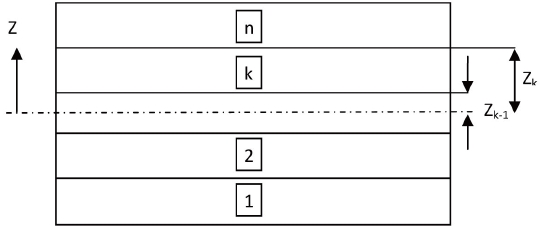
Where n= number of layers of laminated composite curved panel, (
Substituting the standard energy expressions which include strain energy due to bending and transverse shear, work done by external in-plane loads, residual stresses due to hygrothermal conditions and kinetic energy in Lagrange’s equation and on simplifications, the equation of motion for vibration of a laminated composite panel in a hygrothermal environment, subjected to generalized in-plane load
Where ‘q’ is the vector of degrees of freedoms (u, v, w,
Where Ns the static portion of load
Where
The above Equation (6) represents a system of differential equations with periodic coefficients of the Mathieu-Hill type. The development of regions of instability arises from Floquet’s theory which establishes the existence of periodic solutions of periods T and 2T. The boundaries of the primary instability regions with period 2T, where T=2/Ω are of practical importance and the solution can be achieved in the form of the trigonometric series:
Equating the coefficients of the sine and cosine terms leads to a series of algebraic equations for the vectors {a}
Equation (9) represents an eigenvalue problem for known values of
Free Vibration:
Buckling:
2.5 Finite Element Formulation
An eight nodded iso-parametric element is used for static stability analysis of woven fiber composite plates subjected to a hygrothermal environment. Five degrees of freedom
The constitutive relations for the plate and shell subjected to moisture and temperature is given by:
Where
The non-mechanical force and moment resultants due to moisture and temperature are expressed as follows:
Where
in which [
The standard stiffness coefficients for laminated composites are considered in line with [26].
2.7 Strain Displacement Relations
Green-Lagrange’s strain displacement relations are presented in general throughout the analysis. The linear part of the strain is used to derive the elastic stiffness matrix and the non-linear part of the strain is used to derive the geometric stiffness matrix. The total strain is given by:
The linear generalized shear deformable strain displacement relations are
The bending strains kj are expressed as:
The non-linear strain components are as follows:
2.8 Element Elastic Stiffness Matrix
The linear strain matrix {
Where
Where
is a term from Sander’s theory which accounts for conditions of zero strain for rigid body motion in line with Chandrasekhar [29].
Element elastic bending matrix is given by:
2.9 Element Geometric Stiffness Matrix Due to Re sidual Stresses [Krge]
The non-linear strain equations are represented in matrix form:
Where
Equations {
Where
The geometric stiffness matrix due to residual stresses is given by:
Where
In which
2.10 Geometric Stiffness Matrix Due to Applied Loads [Kge]
The first three non-linear strain equations are represented in a matrix form:
{
Where
The geometric stiffness matrix due to applied in-plane loads is given by:
Where
In which:
Where the shape function matrix:
In which the mass moment of inertia
The element load vector due to external transverse static load p per unit area is given by:
The element stiffness matrix, the initial stress stiffness matrix due to hygrothermal load, the mass matrix, geometric stiffness matrix due to applied loads and the load vectors of the element are evaluated by first expressing the integrals in local Natural co-ordinates, ξ and
A computer program based on the MATLAB environment is developed to perform all necessary computations. The composite panel is divided into a two-dimensional array of rectangular elements. The element elastic stiffness and mass matrices are obtained with 2x2 gauss points. The geometric stiffness matrix is essentially a function of the in-plane stress distribution in the element due to applied load and residual stress distribution due to hygrothermal load. The overall element stiffness and mass matrices are obtained by assembling the corresponding element matrices using a skyline technique. A reduced integration technique is adopted in order to avoid possible shear locking.
Numerical results are presented on dynamic behavior of laminated composite panels subjected to hygrothermal loading.
The boundary conditions are described as follows:
Simply supported boundary
S: u=v=w= θy=0 at x=0, a, and u=v= w= θx=0 at y=0, b
S2: u=w= θy=0 at x=0, a, and v= w= θx=0 at y=0, b
The numerical results are presented for symmetric crossply and anti-symmetric angle-ply laminated composite plates/shells using“ S” simply supported conditions, and the comparison with the previous study has been performed for frequency of cross-ply laminated composite shells using the“ S2” simply supported conditions used in that study.
The results are grouped as
Convergence Study
Comparison with Previous Studies
Numerical Results
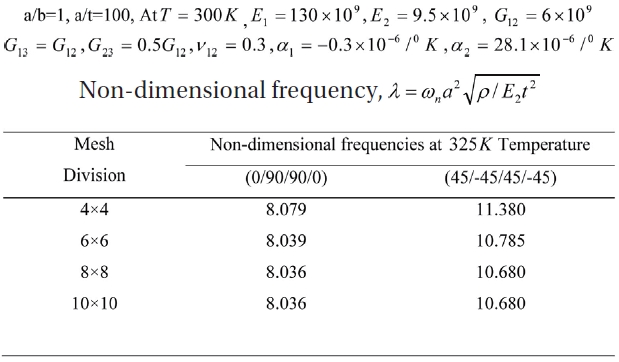
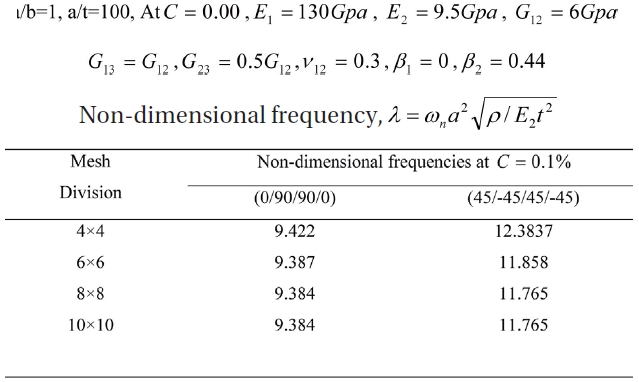
The convergence study is done for non-dimensional frequencies of free vibration of simply supported symmetric cross ply and anti-symmetric angle ply laminated composite plates for elevated temperature and moisture conditions for different mesh divisions as shown in Table 1 and 2.
Convergence of non-dimensional free vibration frequencies for SSSS 4 layer panels for different ply orientations at 325K temperature.
Convergence of non-dimensional free vibration frequencies for SSSS 4 layer panels for different ply orientations at 0.1% moisture concentration.
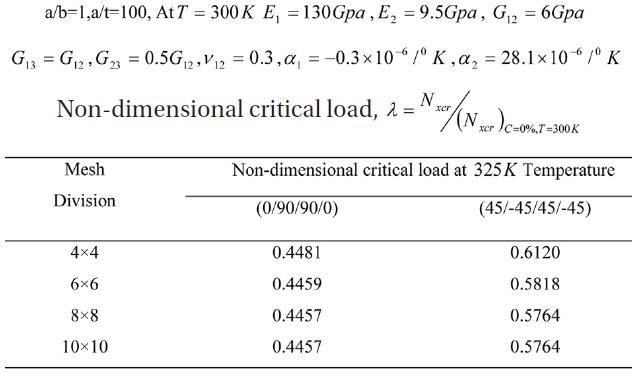
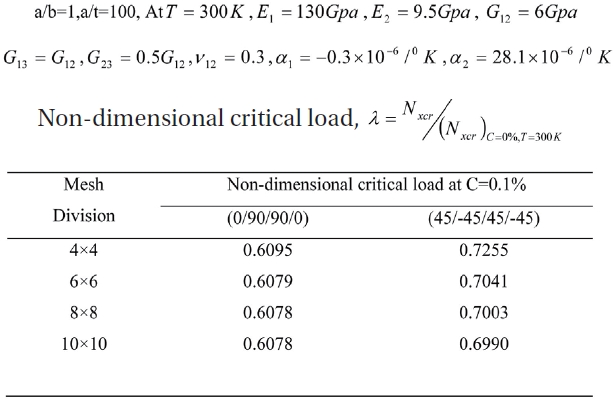
The study is further extended to buckling analysis of laminated composite plates subjected to hygrothermal conditions as presented in Table 3 and 4, and this mesh is employed throughout free vibration, buckling and dynamic stability analysis of laminated composite plates in a hygrothermal environment.
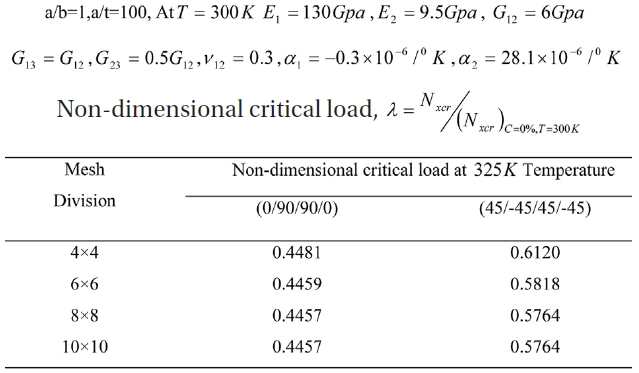
Convergence of non-dimensional critical load for SSSS 4 layer panels for different ply orientations at 325K temperature.
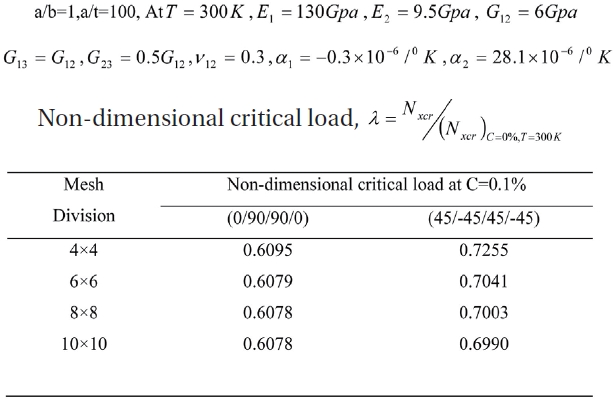
Convergence of non-dimensional critical load for SSSS 4 layer panels for different ply orientations at 0.1% moisture concentration.
Based on the convergence study, a mesh of 8x8 is considered for discretization of the panel for all subsequent analysis.
3.2 Comparison with Previous Studies
Numerical results are carried out to determine the capability of the present formulation to predict the dynamic behaviour and stability of laminated composite panels.
3.3 Vibration of Composite Plates And Shells Subjected To Hygrothermal Environment
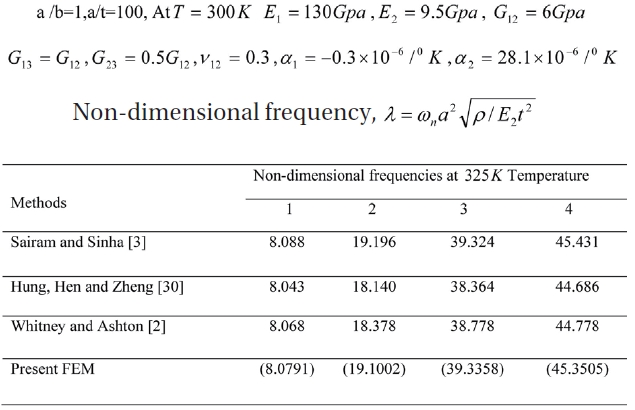
The present formulation is validated for vibration analysis of composites panels for elevated temperature as shown in Table 5.
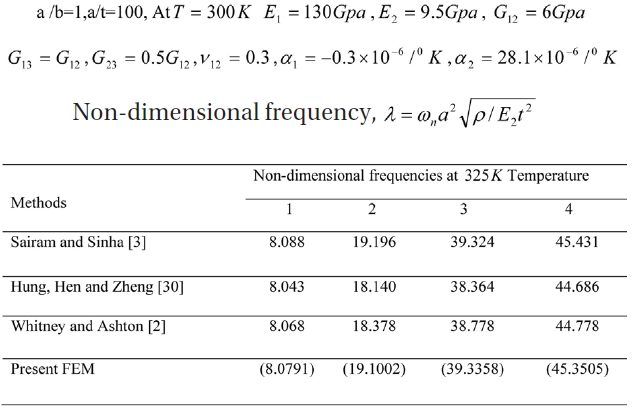
Comparison of non-dimensional free vibration frequencies for SSSS (0/90/90/0) panels at 325K temperature
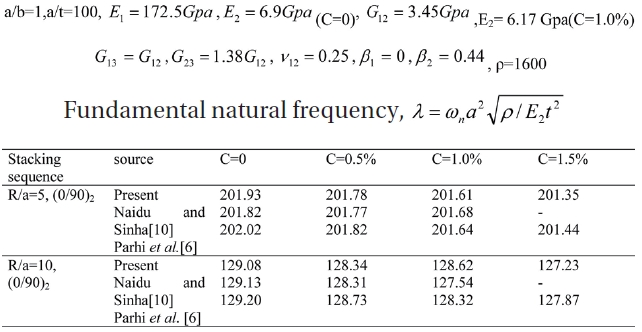
The four lowest non-dimensional frequency parameters due to elevated temperature obtained by the present finite elements are compared with anumerical solution published by Sairam and Sinha [3], Huang et al. [30] using finite element method and Ritz method used by Whitney and Ashton [2]. The non-dimensional frequency parameters for shell with elevated moisture is as shown in Table 6 is compared with results published by Parhi et al. [6] and Naidu and Sinha [10].
[Table 6.] Comparison of natural frequencies for S2 (0/90/90/0) shell at 1% moisture concentration
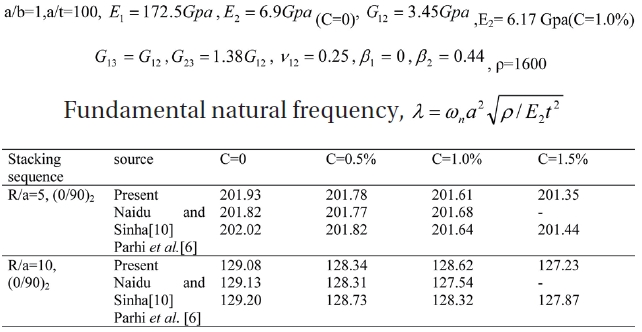
Comparison of natural frequencies for S2 (0/90/90/0) shell at 1% moisture concentration
The present finite element results show good agreement with the previous numerical results published in the literature for free vibration of laminated composite plates and shells subjected to hygrothermal conditions. The present finite element results are in accordance with the previous analytical as well as computational results of other authors.
3.4 Buckling of Composite Plates Subjected To Hygrothermal Environment
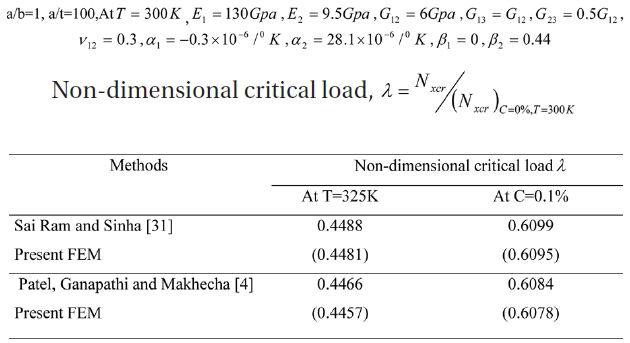
The present formulation is then validated for buckling analysis of laminated composite panels due to hygrothermal loadings with a numerical solution published by Sairam and Sinha [31] and Patel
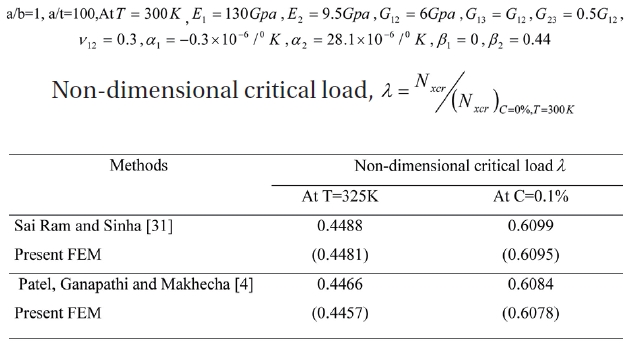
Comparison of non-dimensional critical load for SSSS (0/90/90/0) panels at 325K temperature and 0.1% moisture concentration.
The square panel has four layers of Graphite/Epoxy composite. The present finite element results show good accordance with the previous numerical results published in the literature for buckling of composite plates subjected to hygrothermal loads.
3.5 Numerical Results For Dynamic Stability Of Shells
After validating the formulation, the same is employed to study the dynamic stability effects of laminated composite shells in a hygrothermal environment. Numerical results are presented on the dynamic stability of cross-ply and angle-ply laminated shell to study the effects of various parameters on instability regions. The geometrical and material properties of the laminated shell are as follows:
a=500mm, b=500mm, t=5mm, E1=130Gpa, E2=9.5Gpa, G12=6Gpa, G23/G12=0.5,
The non-dimensional excitation frequency
is used throughout the dynamic instability studies, where
is the excitation frequency in radian/sec. The principal instability regions of laminated composite curved panels subjected to in-plane periodic loads is plotted by the non-dimensional frequency Ω/ω (ratio of excitation frequency to the free vibration frequency) versus the dynamic in-plane load
3.6 Effect of Static Load Factor on Instability Regions of Uniformly Loaded Symmetric Shell
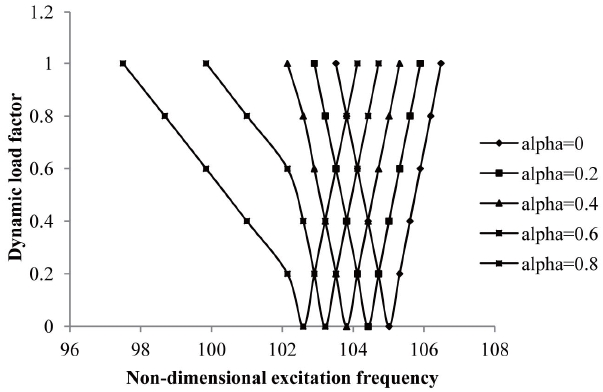
The effect of the static component of load for
Due to an increase of the static component of the load, the instability regions tend to shift to lower frequencies and become wider. With an increase in the static load factor from 0 to 0.8, the excitation frequency is reduced by 2.3%. All further studies are made with a static load factor of 0.2 (unless otherwise mentioned).
3.7 Effects of Temperature on Excitation Frequency
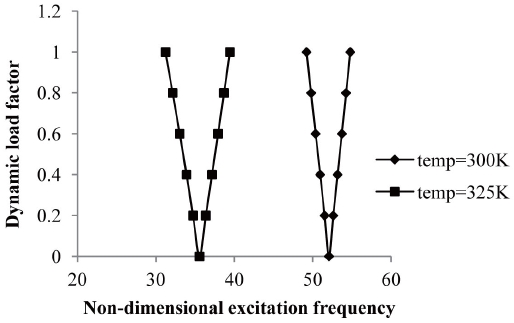
The variation of excitation frequency with dynamic load factors of composite laminated simply-supported symmetric cross-ply square shells subjected to uniform distribution of temperature from 300K and 325K is shown in figure 6.
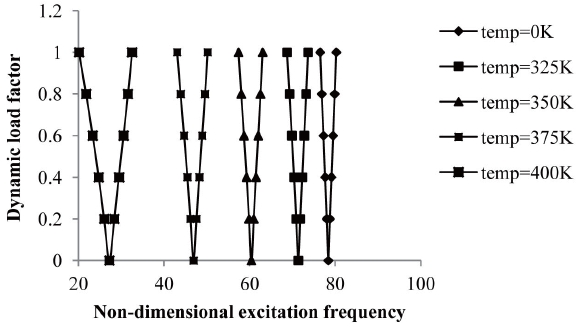
It is observed that the onset of instability occurs earlier with wider DIR for symmetric cross-ply laminated composite panels subjected to elevated temperature compared to composite panels with normal temperature. With an increase in temperature from 300K to 325K, the excitation frequency is reduced by 31.6%. The width of the instability region for laminated panels with elevated temperature is increased by 46.67% from the plate with normal temperature for a dynamic load factor of 0.6. The variation of excitation frequency with dynamic load factors of composite laminated simply-supported anti-symmetric angle-ply square shells subjected to uniform distribution of temperature from 300K, 325K, 350K, 375K and 400K is shown in figure 7.
As shown, the onset of instability occurs earlier with wider DIR for anti-symmetric angle-ply laminated composite shells subjected to elevated temperature compared to composite shells with ambient temperature. With an increase in temperature from 300K to 350K, the excitation frequency is reduced by 65.2%.
3.8 Effects of Moisture on Excitation Frequency:
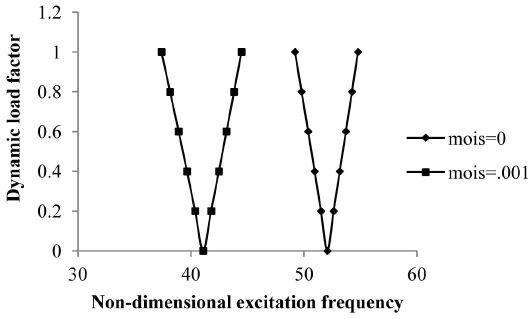
The variation of excitation frequency with dynamic load factors of composite laminated simply-supported symmetric cross-ply curved panels subjected to uniform distribution of moisture concentration from 0% and 0.1% is shown in fig 8.
It is revealed that the onset of instability occurs earlier with wider DIR for symmetric cross-ply laminated composite shells subjected to an elevated moisture condition compared to composite shells with normal moisture. When moisture concentration is increased from 0% to 0.1% then excitation frequency reduces by about 21%. The width of the instability region for laminated shells with elevated moisture is increased by 46.67% from the shell with ambient moisture for a dynamic load factor of 0.6. The variation of excitation
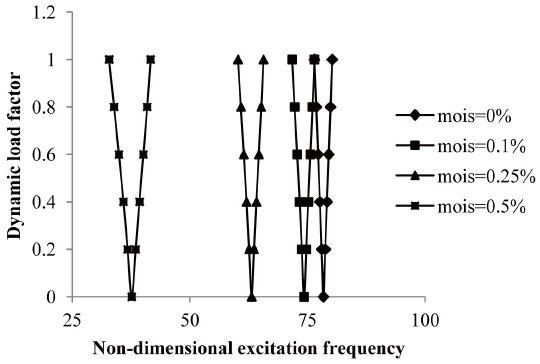
frequency with dynamic load factors of composite laminated simply-supported anti-symmetric angle-ply curved panels subjected to uniform distribution of moisture concentration from 0%, 0.1%, 0.25% and 0.5% is shown in fig 9.
It is revealed that the onset of instability occurs earlier with wider DIR for anti-symmetric angle-ply laminated composite shells subjected to an elevated moisture condition compared to composite shells with a normal moisture concentration. When moisture concentration is increased from 0% to 0.25% then excitation frequency reduces by about 49.3%.
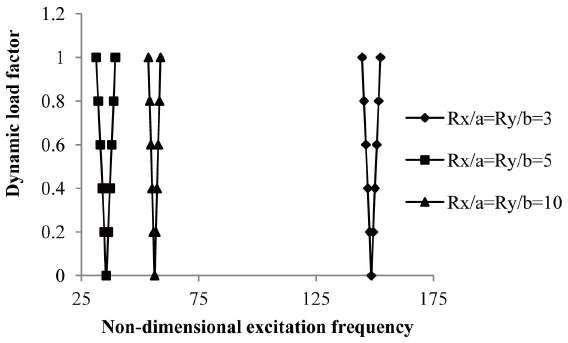
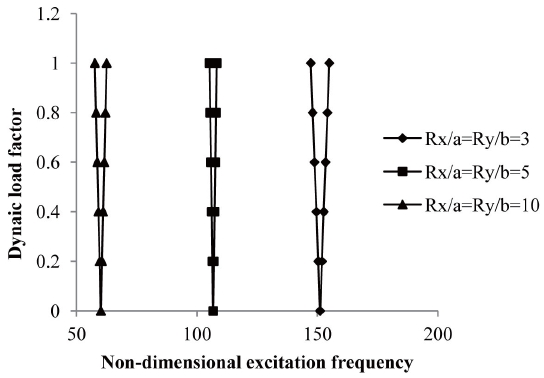
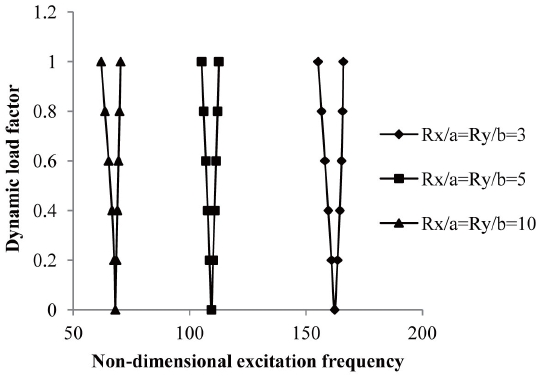
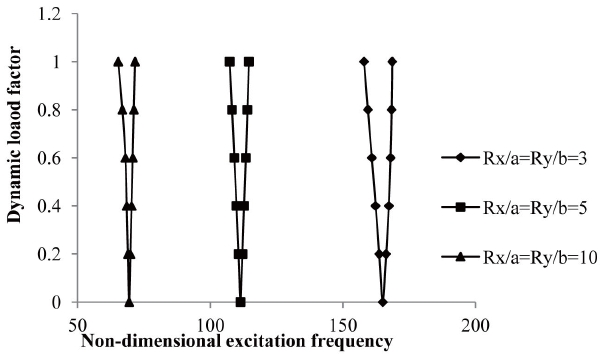
3.9 Effects of Curvature on Excitation Frequency
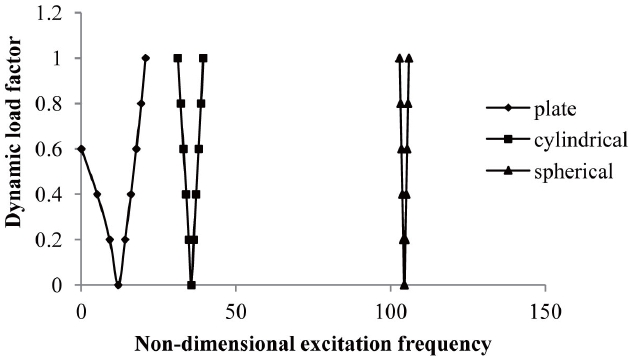
Studies have also been made (Fig 10) for the comparison of instability regions for different shell geometries.
The effect of curvature on instability regions of different curved panels for a/b=1, flat panel (a/R
3.10 Effects of Aspect Ratio on Excitation Frequency
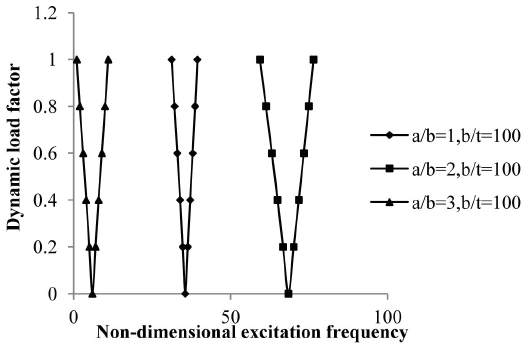
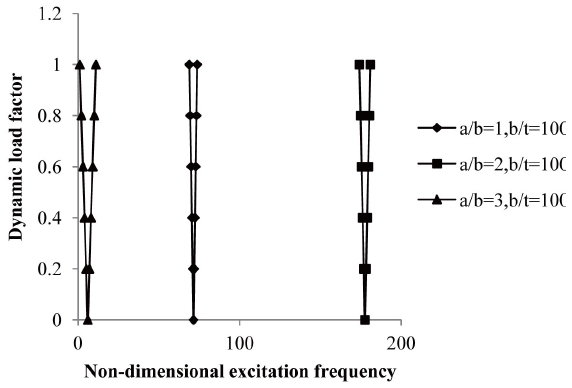
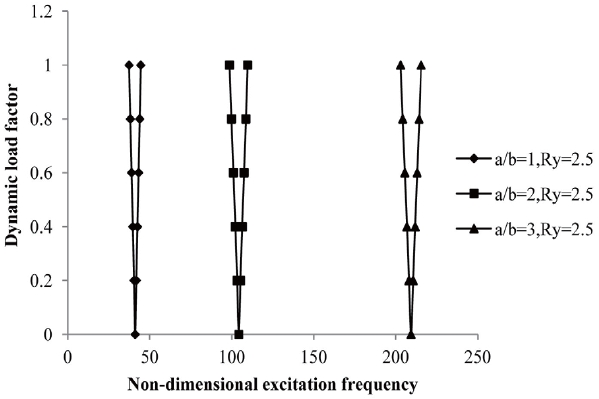
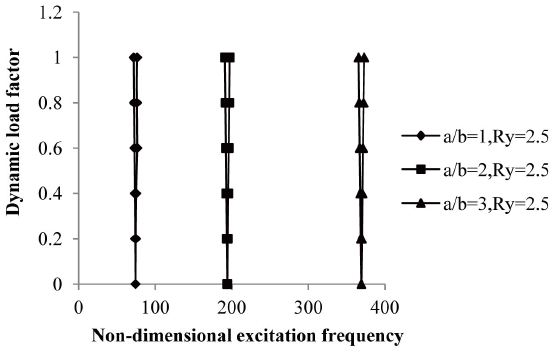
The variation of instability regions with dynamic load factors of composite laminated simply supported symmetric cross-ply and anti-symmetric angle-ply shells with excitation frequency subjected to a uniform distribution of elevated temperature with different aspect ratio (a/b =1, 2 and 3) are shown in figures 11 and 12.
It is observed that the onset of instability occurs earlier with a decrease of the aspect ratio with a decreasing width of the instability region. The onset of instability occurs later for rectangular anti-symmetric angle-ply laminated composite shells rather than square shells subjected to elevated temperatures but with wider instability regions. The width of instability regions increased marginally for rectangular plates rather than square plates with a uniform rise in temperature and moisture concentrations. The increase in aspect ratio shifts the frequency of the instability region to higher values and reduces the dynamic stability strength. The variation of the instability region with dynamic load factors of composite laminated simply supported symmetric cross-ply and antisymmetric angle-ply shells with an excitation frequency subjected to uniform distribution of elevated moisture with different aspect ratios (a/b =1, 2 and 3) are shown in figures 13 and 14.
It is observed that the onset of instability occurs earlier
with a decrease of the aspect ratio with decreasing width of the instability region. The onset of instability occurs later for rectangular anti-symmetric angle-ply laminated composite shells rather than square shells subjected to elevated moisture but with wider instability regions. The width of instability regions increased marginally for rectangular shells rather than square shells with a uniform rise in moisture concentration. The increase in aspect ratio shifts the frequency of instability region to higher values and reduces the dynamic stability strength.
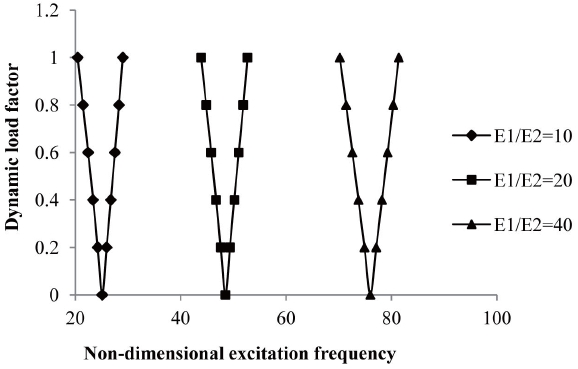
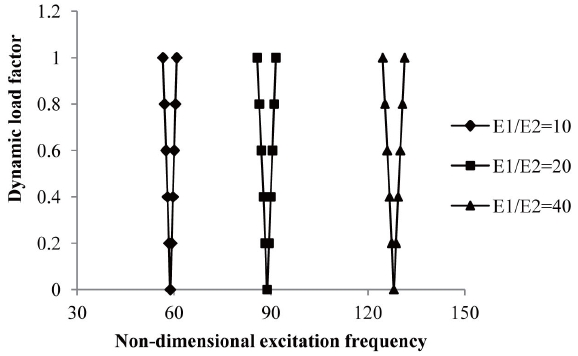
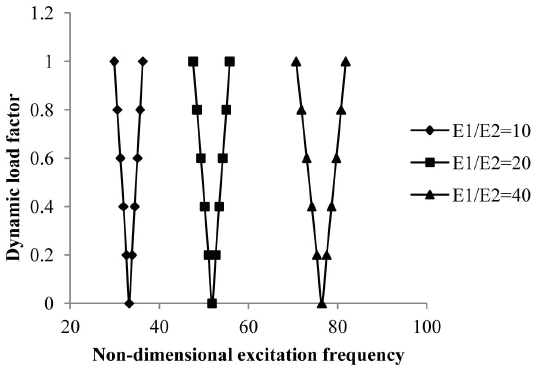
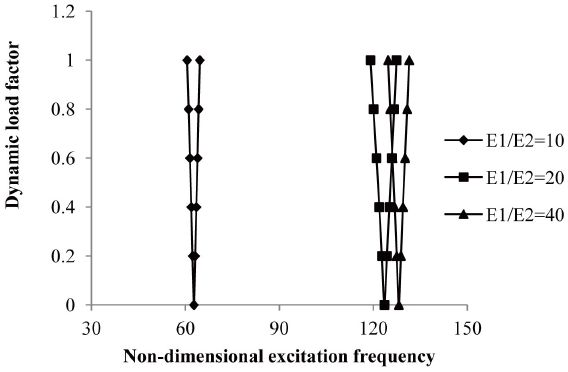
3.11 Effects on Degree of Orthotropy
The variation of excitation frequency with dynamic load factors of composite laminated simply supported symmetric cross-ply and for anti-symmetric angle-ply shells subjected to uniform distribution of temperature are shown in figures 15 and 16.
The effect of the degree of orthotropy is studied for E1/ E2 = 40, 20, 10 keeping other material properties constant. It is observed that the onset of instability occurs later with an increase of degree of orthotropy for symmetric cross-
ply and anti-symmetric angle-ply laminated composite shells subjected to elevated temperature but with wider instability regions. The excitation frequency is reduced but the instability region is wider in cross-ply symmetric laminate rather than anti-symmetric angle-ply laminate. The variation of excitation frequency with dynamic load factors of composite laminated simply supported symmetric cross-ply and for anti-symmetric angle-ply shells subjected to uniform distribution of moisture are shown in figures 17 and 18.
The effect of degree of orthotropy is studied for E1/E2 = 40, 20, 10 keeping other material properties constant. It is observed that the onset of instability occurs later with an increase of degree of orthotropy for symmetric cross-ply and anti-symmetric angle-ply laminated composite shells subjected to uniform distribution of moisture but with wider instability regions. The excitation frequency is reduced but the instability region is wider.
The variation of excitation frequency with dynamic load
factosr of composite laminated simply supported symmetric cross-ply and for anti-symmetric angle-ply shells subjected to uniform distribution of temperature are shown in figures 19 and 20.
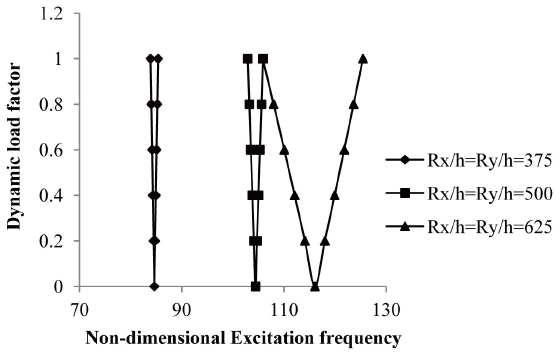
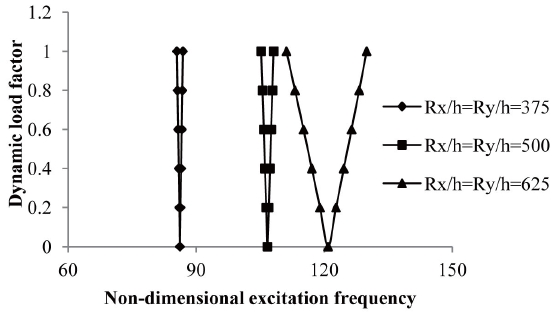
The effect of radius to thickness ratio is studied for R
increase of Ry/h ratio but with wider instability regions. The excitation frequency is reduced but the instability region is narrower in cross-ply symmetric laminate rather than antisymmetric angle-ply laminate in elevated temperatures. The variation of excitation frequency with dynamic load factors of composite laminated simply supported symmetric crossply and for anti-symmetric angle-ply shells subjected to uniform distribution of moisture are shown in figures 21 and 22.
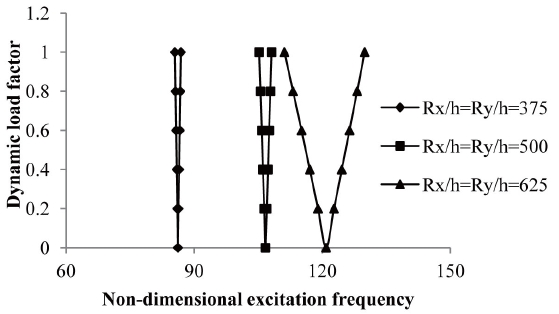
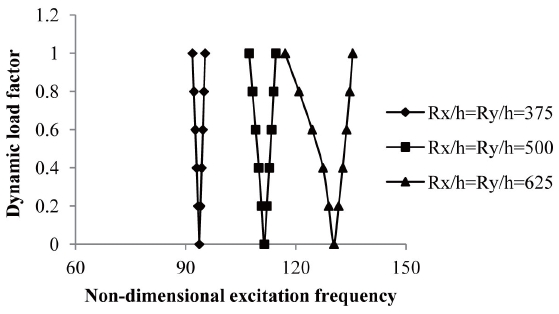
It is observed from the figure that the onset of dynamic instability region occurs earlier with a decrease of the Ry/h ratio but with a narrower instability region. The excitation frequency is reduced but the instability region is narrower in cross-ply symmetric laminate rather than anti-symmetric angle-ply laminate in elevated moisture.
3.13 Effect of Shallowness Ratio
The variation of excitation frequency with dynamic load factors of composite laminated simply supported symmetric cross-ply and for anti-symmetric angle-ply shells subjected to uniform distribution of temperature are shown in figures 23 and 24.
The effect of the shallowness ratio on instability regions is studied for R
The effect of the shallowness ratio on instability regions is studied for R
3.14 Effect of Ply-Orientation
The variation of instability regions with dynamic load factors of composite laminated simply supported antisymmetric angle-ply shells with excitation frequency subjected to uniform distribution of temperature with different ply orientations is shown in fig 27.
It is observed that the onset of instability occurs earlier for anti-symmetric angle-ply composite shells with 0 degree
of ply orientation than for shells with a higher degree of ply orientation subjected to elevated moisture conditions but with narrow DIR. The value of ply orientation for which the instability region is narrower is 45 and for the wider DIR the ply orientation value is 0. The instability region is less wide for increase in lamination angle but the excitation frequencies are decreased with a decrease in uniform temperature distribution. The ply orientation for 00 seems to be the preferential ply orientation for this lamination sequence. The variation of instability regions with dynamic load factors of composite laminated simply supported anti-symmetric angle-ply shells with excitation frequency subjected to uniform distributions of moisture with different ply orientations is shown in figure 28.
It is observed that the onset of instability occurs earlier for anti-symmetric angle-ply laminated composite shells with 0 degree of ply orientation than the shells with a higher degree of ply orientation subjected to elevated moisture conditions but with narrow DIR. The value of the ply orientation for which the instability region is narrower is 45 and for the wider DIR the ply orientation value is 0. The instability region is less wide for increases in lamination angle but the excitation frequencies are decreased with a decrease in uniform moisture concentration.
A general formulation for vibration, buckling and parametric resonance characteristics of laminated composite curved panels subjected to in-plane periodic load under hygrothermal environment is presented:
The excitation frequencies of laminated composite panels decrease with an increase of temperature due to reduction of stiffness for all laminates.
The excitation frequencies of laminated composite panels also decrease substantially with an increase of moisture concentration for all laminates.
Due to the static component of loads, the onset of instability shifts to lower frequencies with wide instability regions of the laminated composite panels.
The instability region is observed to be influenced by the lamination angle of the laminated composite curved panel under hygrothermal loads.
Increasing the aspect ratio shifts the frequencies of instability regions to higher values and reduces the dynamic stability strength of the laminated composite panel.
The width of dynamic instability regions is smaller for square laminated composite panels than rectangular panels with hygrothermal load.
The excitation frequency increases with the introduction of curvatures from flat panel to doubly curved panel in hygrothermal environment.
From the present studies, it is concluded that the instability behavior of laminate composite plates and shells is greatly influenced by the geometry, lamination parameters and hygrothermal conditions. Therefore the designer has to be cautious while dealing with structures subjected to hygrothermal loading. This can be utilized to the designer’s advantage during the design of woven fiber laminated composite structures in a hygrothermal environment.