The eclipsing nature of V700 Cyg (OV 26, 2MASS J20310525 3847006, CCDM J20311 3847A, WDS J20311 3847A) was discovered by Whitney (1952) who classified it as a W UMa-type binary star with a period of 0.d340048. The first photoelectric BV light curves with an O’Connell effect (Max II fainter than Max I) were secured by Niarchos et al. (1997) who studied global photometric properties of the system through light curve synthesis as well as period study. According to those authors, V700 Cyg is a W UMa W-subtype binary star with the spectral type of G5V and an orbital inclination of 79.9° . The more massive 0.92
In recent years, V700 Cyg was revisited by Qian (2003), Molik & Wolf (2004), Xiang et al. (2009) and Yang & Dai (2009). Qian (2003) obtained new light elements (
Surveying the historical period studies performed by the investigators above, we note the following: 1) even concurrent studies (Xiang et al. 2009, Yang & Dai 2009) made with nearly the same times of minima do not show consistency for the period of the seemingly cyclic change; and 2) numerous timings before and after the recent period studies of Xiang et al. (2009) and Yang & Dai (2009) have been published (e.g., see Table 1 and the references therein). In this paper, we perform an intensive reanalysis of all the published timings available to us, including our new two timings and 59 others calculated from the super wide angle search for planets (SWASP) observations. Two cyclic changes superposed on a weakly constrained upward parabolic variation are suggested. The following is a discussion of the implications of existing working hypotheses.
2. OBSERVATIONS AND TIMES OF MINIMA
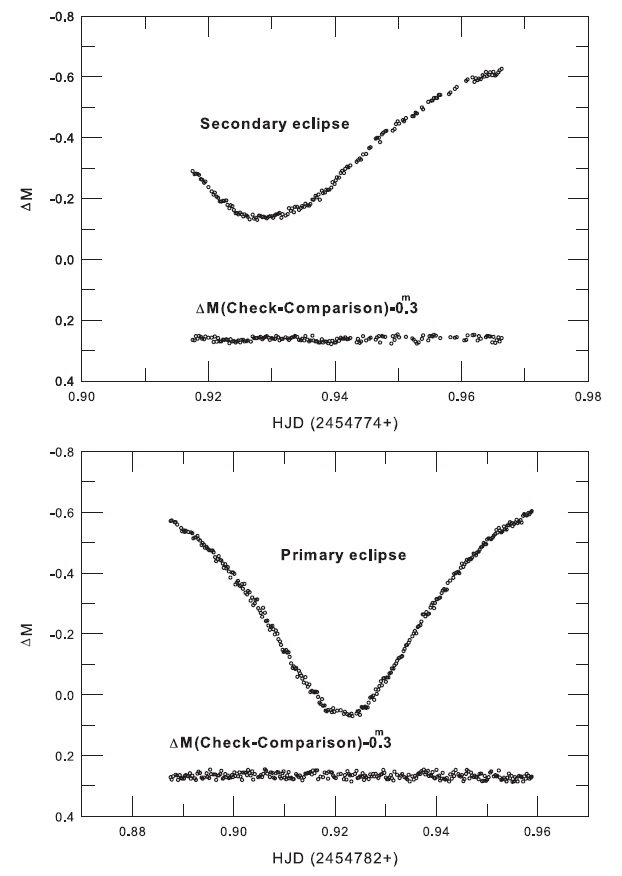
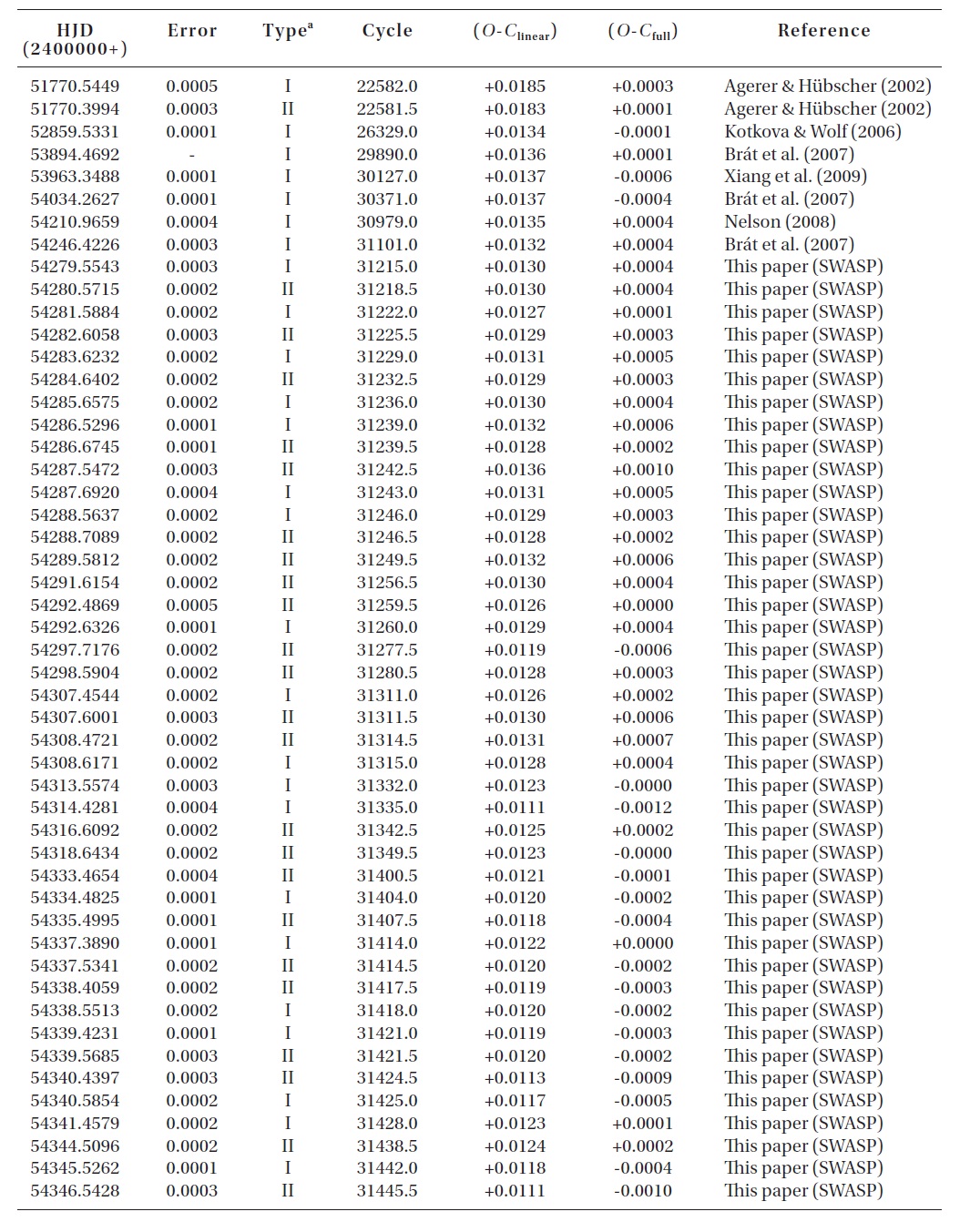
The CCD photometric observations of V700 Cyg for the purpose of timing determination were made on the nights of November 4 and 12 in 2008 with the 35 cm campus station reflector at the Chungbuk National University Observatory in Korea. The telescope was equipped with an SBIG ST-8 CCD imaging system and electrically cooled with a 19' × 12'field of view. No filters were used in our observations. GSC 3152-527 and GSC 3153-193 were chosen as the comparison and check stars, respectively. The instrumentation used and reduction method for the raw CCD frames have been described in detail by Kim et al. (2006). The resultant standard error of our observations (check minus comparison) was approximately ± 0.m009. The light curves for the observations are shown in Fig. 1.
From our observations using the conventional Kwee & van Woerden (1956, KW) method, two times of minimum light were determined. In addition, we researched whether
V700 Cyg has been observed in survey works such as the all sky automated survey (ASAS) and the SWASP. Fortunately, V700 Cyg is identified as 1SWASP J203105.27 384701.8 in the SWASP public archive that is available at the Web1 and managed by the SWASP community. Using the SWASP data observed from June 14 to October 25 in 2007, we calculated a total of 59 timings (27 for the primary timing and 32 for the secondary timing) by the KW method.
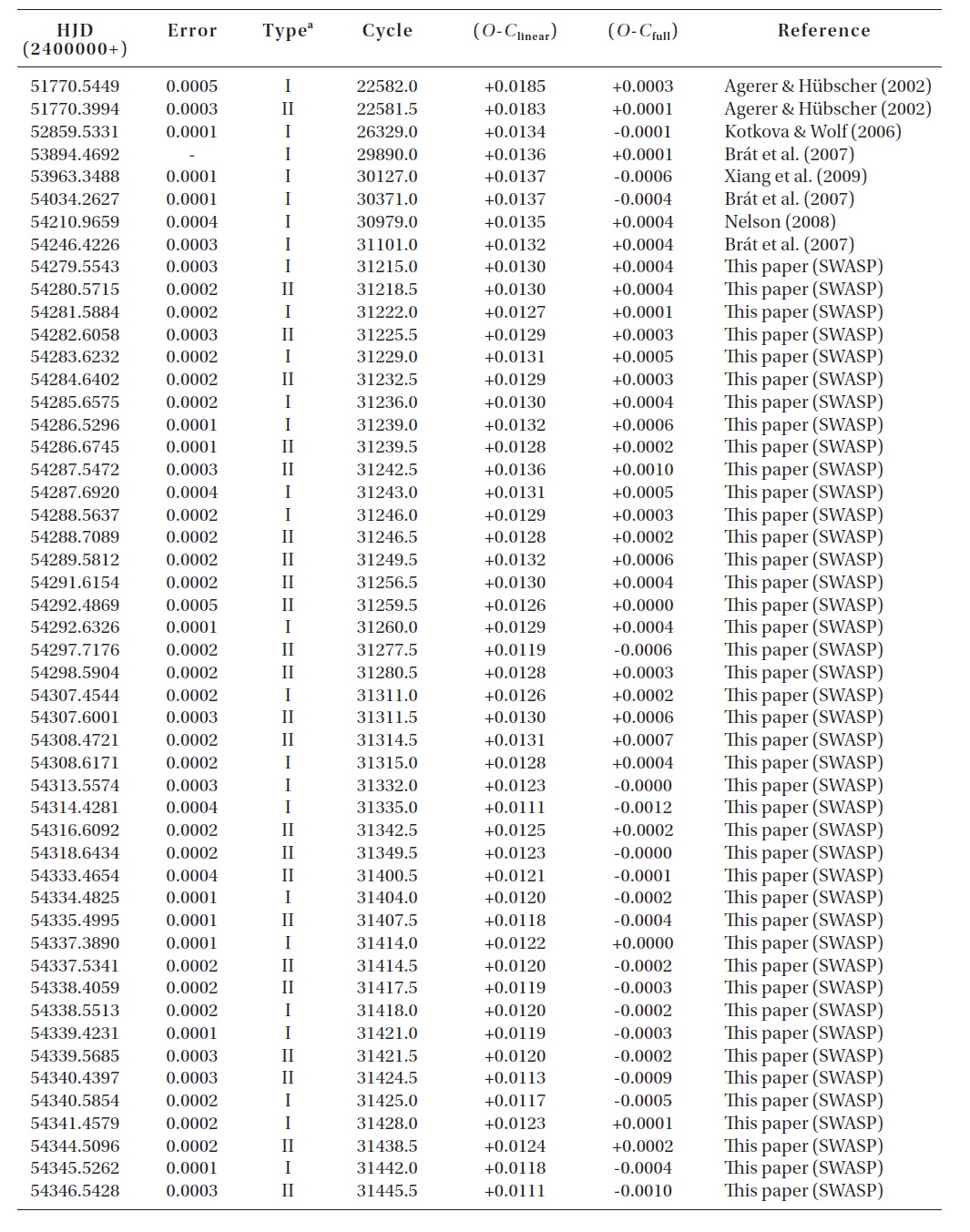
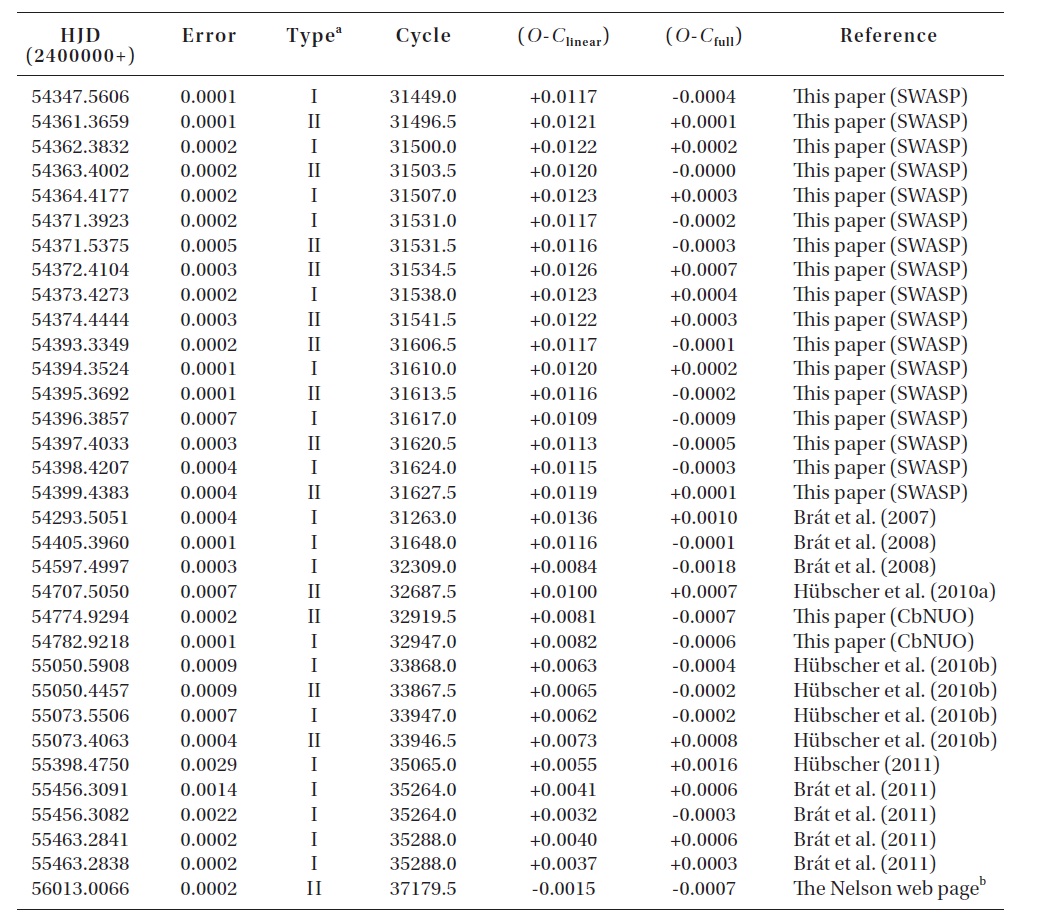
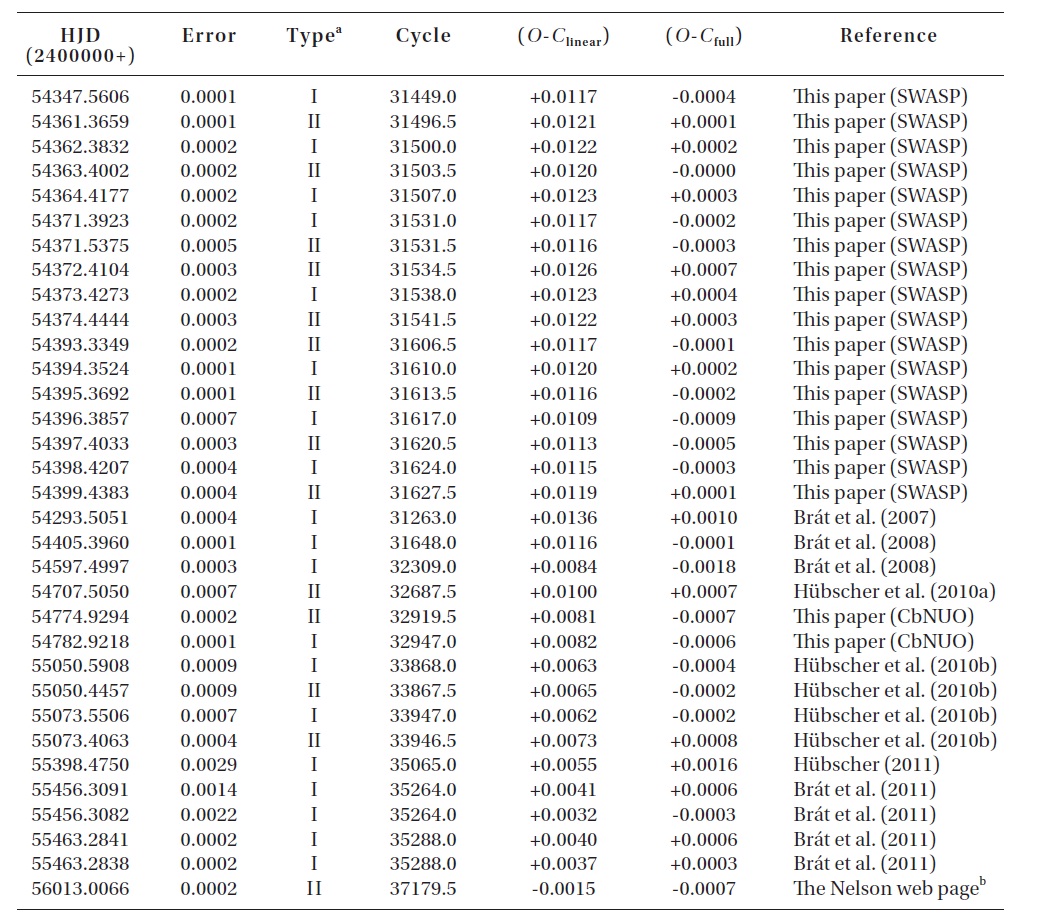
The CCD times of minima of V700 Cyg not listed in Yang & Dai (2009) or published after their study.
1http://www.wasp.le.ac.uk/public/lc/index.php
To investigate the period variation of V700 Cyg, a total of 148 (9 visual, 14 plate, 7 photographic, and 118 photoelectric and CCD) times of minimum light (including ours and those from the SWASP) were collected from a modern database (Kreiner et al. 2001) and from the recent literature. Table 1 lists only the photoelectric and CCD minima, which were not compiled by Yang & Dai (2009) or published after their study.
(Continued)
The (
The (
[Table 2.] The Final solutions of Eqs. (3) and (4).
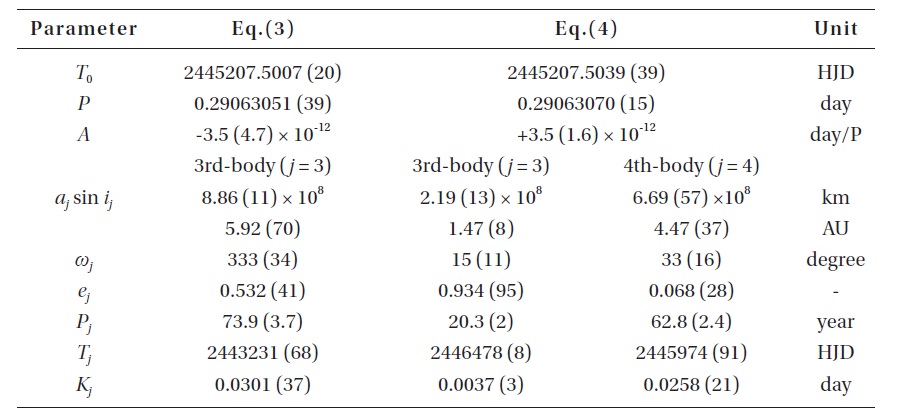
The Final solutions of Eqs. (3) and (4).
to secondary timings and vice-versa. Xiang et al. (2009) used the ephemeris (Eq. 1) from Kreiner et al. (2001) and improved it as follows:
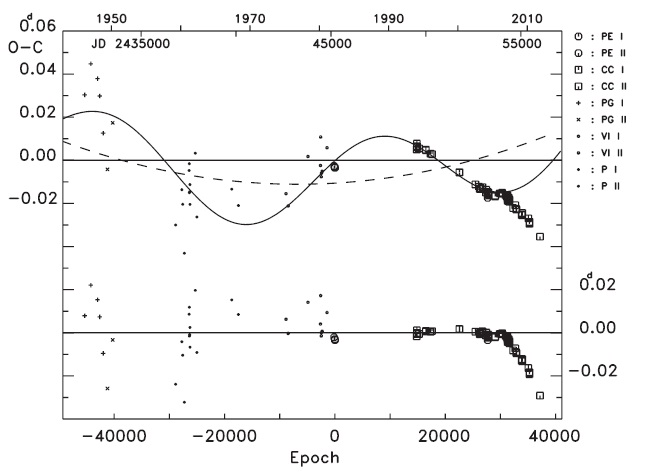
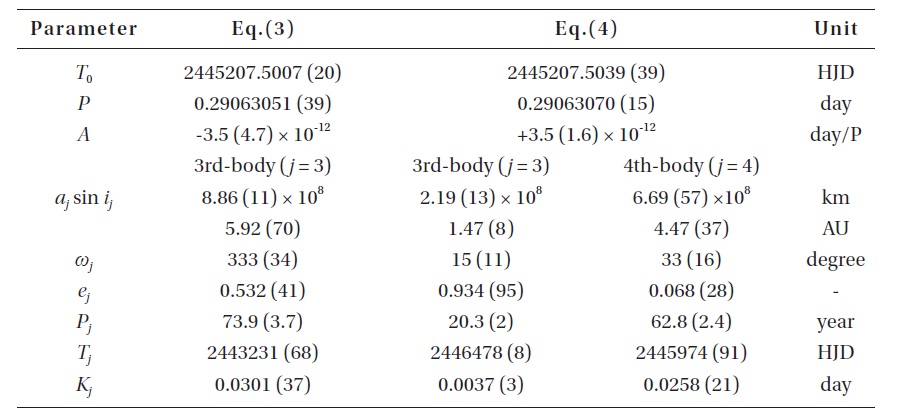
The dashed and solid lines in Fig. 2 denote the linear (plus quadratic) and full terms, respectively, from Eq. (2). The residuals from Eq. (2) were plotted at the bottom of Fig. 2 where the recent timings (since 2007y) have been clearly deviating from the ephemeris, which implies that Eq. (2) should be revised and/or the period change of V700 Cyg may be more complicated.
To understand the general period change behavior, we tried to fit all of the times of minima to a quadratic plus LTE ephemeris described as:
where τ 3 is the light-time due to the assumed third body and includes the five orbital parameters (
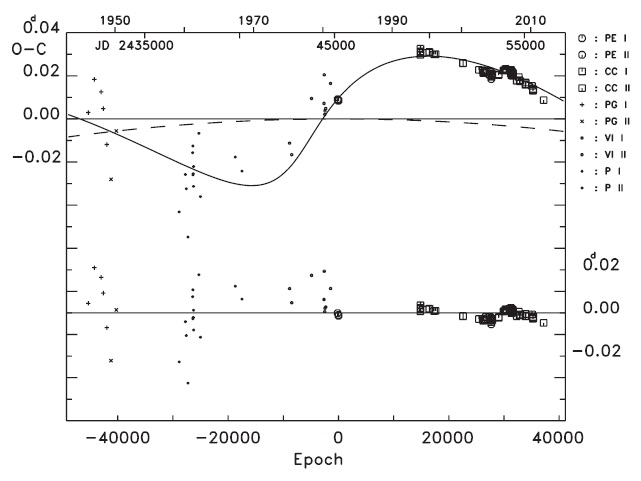
lines representing the quadratic and LTE terms, respectively. The residuals from the full terms were plotted in the bottom of Fig. 3.
As shown in Fig. 3, Eq. (3) provides a more satisfactory fit to the observed timings than Eq. (2). The cyclic period is calculated as 73.y9 (± 3.y7), which is 27.y9, 34.y8 and 19.y2 longer than those provided by Molik & Wolf (2004), Xiang et al. (2009) and Yang & Dai (2009), respectively. Note that the photoelectric and CCD residuals at the bottom of Fig. 3 are distributed in an oscillatory pattern with a small amplitude of about 0.d003 and with a short period of about 20y. The standard deviation for the photoelectric and CCD residuals is σ = ± 0.d0019, which is 4 times larger than the nominal error (± 0.d0005) of the modern photoelectric and CCD timing observations. The coefficient of the quadratic term has a value smaller than its standard error (with a negative sign), which is contrary to the findings of Xiang et al. (2009) and Yang & Dai (2009). This result implies that the secular
variation is not well constrained by the present timing data because the quasi-sinusoidal variation is dominant and also because the secondary oscillatory pattern is not considered in Eq. (3).
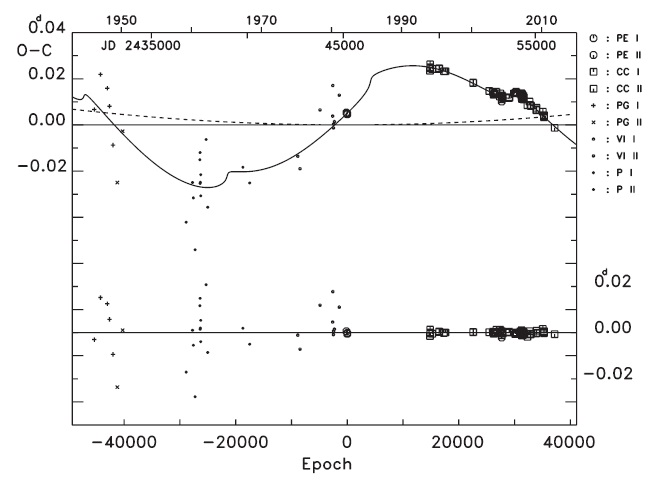
To find the variation characteristics of the small oscillation in Fig. 3, we used two LTEs ephemeris, which are expressed by simply adding τ 4 to Eq. (3) as follows:
where τ 4 is the light-time due to the assumed fourth body and also includes the five orbital parameters (a123 sin
From the coefficient (
In the above section, we have decoupled two cyclic terms via Eq. (4) from the observed (
Two rival theories may explain these cyclic period
[Table 3.] The basic parameters for the hypothetical third and fourth bodies in the V700 Cyg system.
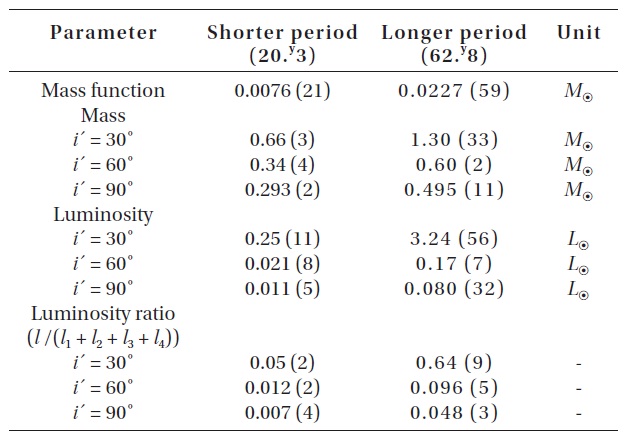
The basic parameters for the hypothetical third and fourth bodies in the V700 Cyg system.
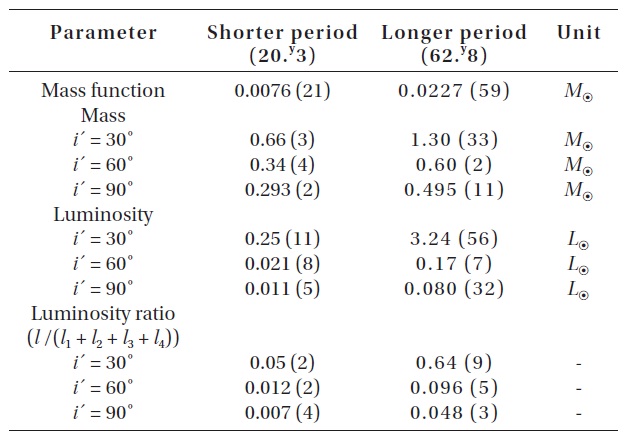
changes: 1) The LTEs are caused by additional third and fourth bodies in the V700 Cyg system; or 2) the Applegate (1992) mechanism, which was improved by Lanza et al. (1998). If the LTEs are assumed to be the mechanism to produce two cyclic period changes, then mass functions, masses and bolometric luminosities for different inclinations of two tertiary bodies were calculated by using the absolute dimension (
[Table 4.] The Applegate model parameters for the shorter and longer periods.
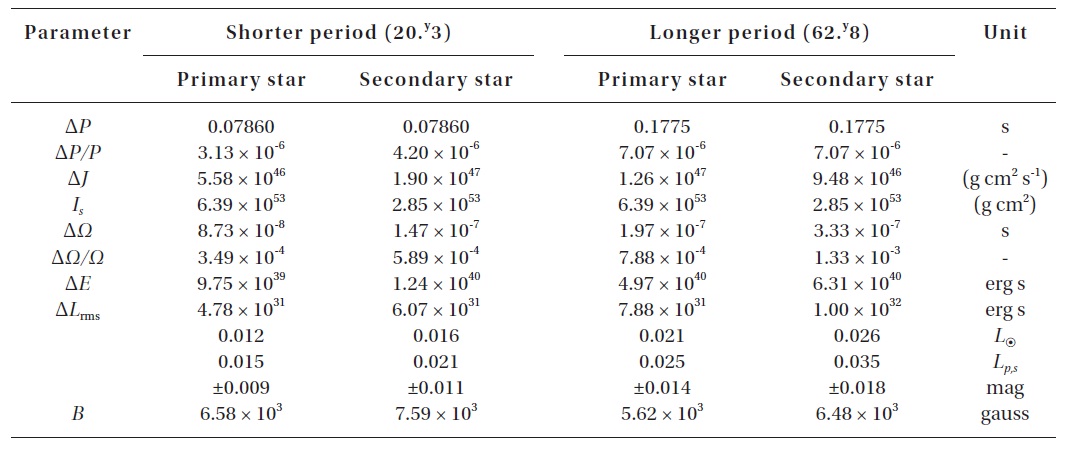
The Applegate model parameters for the shorter and longer periods.
mean that the additional bodies revolve around the mass center of the system in planes nearly coplanar with the orbital plane of the eclipsing pair.
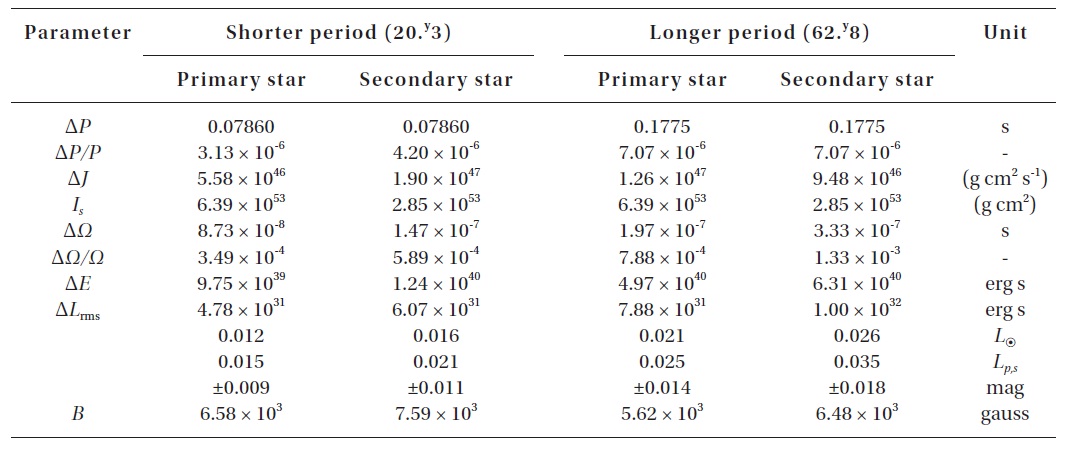
The Applegate (1992) model can alternatively explain the cyclical components of the period variability. According to this theory, the cyclic changes in the magnetic dynamo activity of tidally locked cool stars in binary systems can produce small cyclic orbital period modulations. Using the modulation periods and amplitudes listed in Table 2 and adopting the absolute dimensions explained above, the model parameter variations needed to change the orbital period for V700 Cyg can be obtained from the formula provided by Applegate (1992). The calculations were made with the assumption that two cyclical period changes are produced by both components. Table 4 lists the resultant Applegate parameters where the root mean square (RMS) luminosities converted to magnitude scale were calculated with the formula provided by Kim et al. (1997). The parameters in Table 4 show that the Applegate mechanism could operate well in both the primary and secondary components for both cyclic period changes, although the RMS luminosity variations relative to the luminosities of the primary and secondary stars are 3 times smaller than the nominal value (Δ
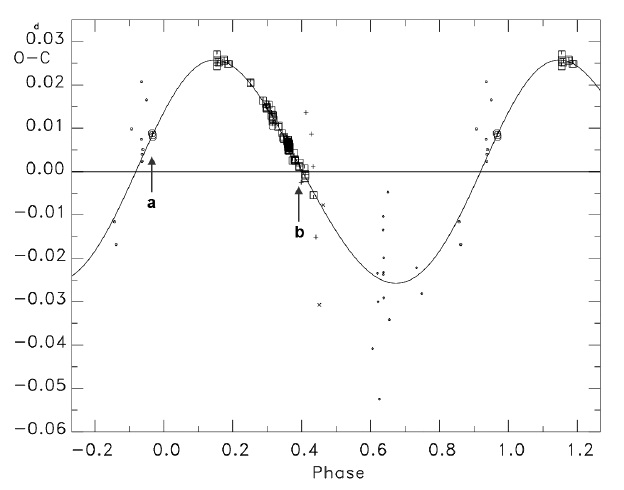
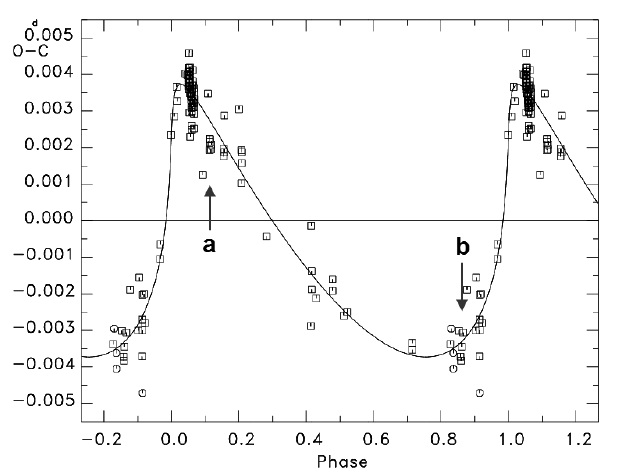
The observation epochs of light curves by Niarchos et al. (1997) and Yang & Dai (2009) are marked as ‘a’ and ‘b’ with an arrow in Figs. 5 and 6, respectively. As shown in Fig. 5, the light curves from Niarchos et al. (1997) were obtained from a position somewhat distant from the ascending nodal point in the 63.y4 sinusoidal curve, but Yang & Dai’s (2009) obtained their light curves just near the descending nodal point. Because the two epochs are near nodal points and the Applegate RMS brightness variation calculation is small, the expectation is that the light curves at the two epochs are symmetrical, but the reality described above is different. In Fig. 6, we see that the light curves of Niarchos et al. (1997) and Yang & Dai (2009) were observed near the bottom and top, respectively, of the highly quasi-sinusoidal curve with the 20.y4 shorter period. If the Applegate mechanism is assumed to be a cause of the shorter period modulation, then any light curves at the positions should show as asymmetrical because of the highly enhanced magnetic activities, but the perfect symmetric light curves from Yang & Dai (2009) defy that explanation. Based on these discussions, the preferred explanation is that the geometrical LTEs (due to the third and fourth stars) cause the two cyclic period variations, although the Applegate mechanism cannot be ruled out based on the presently available insufficient data (light curves and timings).
To understand the dynamical picture of this active W UMa binary system in detail, we analyzed a total of 148 timings of V700 Cyg, including our two timings and 59 others that were calculated from the SWASP observations. It was found that the orbital period of the system has varied over about 66y in two cyclical components superposed on a weakly constrained upward parabola. Three decoupled components of the period variability were investigated.
The secular period increase of + 8.7 (± 4.0) × 10-9 day/year is one order of magnitude lower than those obtained previously (Xiang et al. 2009, Yang & Dai 2009), indicating that the secular period increase over 66y is not convincingly revealed with the present timing data. The weak secular period increase of V700 Cyg may be a special feature in that the secular period increases (or decreases) of most of W UMa contact binaries are approximately one or two orders of magnitude larger than that of V700 Cyg (e.g., Wolf et al. 2000, Qian 2003, Kim et al. 2003, Lee et al. 2008). In general, W UMa binaries are known to suffer from a secular period decrease via angular momentum loss (AML) due to magnetic braking (van’t Veer 1979, Rucinski 1982, Bradstreet & Guinan 1994, Maceroni & van’t Veer 1991, Stepien 1995, 2006, Demircan 1999). Mass and energy exchanges through the connecting neck between the two components are also possible, resulting in a thermal relaxation oscillation (TRO; Lucy 1976, Flannery 1976, Robertson & Eggleton 1977). If we assume that the two mechanisms occur concurrently in any contact binary system and that the size of the period decreasing rate predicted by the AML is slightly smaller than that of the increase rate caused by a mass transfer from the less massive component to the more massive component, then a weak secular period increase could possibly be observed (as in the V700 system). Under this assumption, an observed secular period rate can be formulated as the sum of the period change rates of the two mechanisms as follows:
where the first and second terms in the right side represent the period variation rates due to magnetic braking (mb) and mass transfer (mt), respectively. In the case of V700 Cyg, the decreasing period rate caused by the magnetic braking was determined to be -5.8 × 10-8 day/year with the formula provided by Bradstreet & Guinan (1994). Therefore, the secular period increase by a mass transfer from the less massive star to the more massive one is calculated with Eq. (5) as 6.7× 10-8 day/year, which is comparable to those of other W UMa contact binaries (e.g., Wolf et al. 2000, Qian 2003, Kim et al. 2003, Lee et al. 2008). If this picture is true of V700 Cyg, then the system is on an evolutionary phase in that the increasing period rate by a secular mass transfer from the less massive hot star to the more massive cool one is comparable to or slightly larger than the decreasing rate by a secular AML (due to magnetic braking). Future timings are important in resolving whether this conjecture is realistic.
In addition to the secular period increase, the complex period variations of V700 Cyg were decoupled into two cyclical components via two LTE ephemeris. The inner orbit has a period of 20.y3 (
The low luminosities of the suggested bodies could imply that they are revolving around the mass center of the system in planes nearly coplanar with the orbital plane of the eclipsing pair.
The Applegate model parameters in Table 4 indicate that the RMS luminosity variations relative to the luminosities of the primary and secondary stars are 3 times smaller than the nominal value (Δ