As it is known, the motivation for the Chinese postman problem (CPP) came from the job of a postman. Starting the post office, the postman must cover each street in his area at least once, and then end up at the same place where he began his route. Subject to this condition, the postman wishes to seek the shortest way to complete his assigned route of streets. This problem is known as the CPP, since it was first considered by a Chinese mathematician, Kuan (1962).
The CPP is one of the classical problems of network optimization. There are many real-world situations that can be reduced as CPP. For example, a driver of a watering car or a garbage truck, he wishes to choose his route in such a way that traverses as little as possible. It is important to study this problem both from theoretical and practical points of view. The deterministic CPP has been well studied and many efficient algorithms have been developed by many researchers, such as Edmonds and Johnson (1973), Minieka (1979), Lin and Zhao (1988), Nobert and Picard (1996), Pearn and Chou (1999), etc.
However, because of failure, the lack of history data, or other reasons, some uncertain factors will appear in many situations. For example, because of the weather, traffic, the time costed for the postman on the road is uncertain. As a result, it is not suitable to employ classical approaches in these situations.
Fortunately, in order to deal with human data, such as empirical estimation, uncertainty theory was proposed by Liu (2007). From then on, uncertainty theory has provided a new approach to deal with uncertain factors in programming problems. Liu (2012) said that “when the sample size is too small (even no-sample) to estimate a probability distribution, we have to invite some domain experts to evaluate their belief degree that each event will occur. Since human beings usually overweight unlikely events, the belief degree may have much larger variance than the real frequency and then probability theory is no longer valid. In this situation, we should deal with it by uncertainty theory.
In this paper, the weight data can only be obtained from expert’s empirical estimation. We regard weight as uncertain variable. Obviously, we cannot get a shortest route in the normal sense. We introduce the concepts of expected shortest route,
Within the framework of uncertainty theory, these models can be transformed into their corresponding deterministic forms. The transformed models can be solved based on Fleury algorithm and Dijkstra algorithm.
The remainder of this paper is organized as follows. Section 2 presents some basic concepts and properties selected from uncertainty theory. In Section 3, the uncertain Chinese postman problem is described. In Section 4, expected shortest model and
In order to describe uncertain phenomena, especially expert data and subjective estimation, Liu (2007) proposed uncertainty theory in 2007. From then on, uncertainty theory has received great attention. For instance, Liu (2008) proposed uncertain processes which is a sequence of uncertain variables indexed by time or space. Later, in order to deal with differentiation and integration of functions of uncertain processes, uncertain calculus was initialized by Liu (2009a). Based on uncertain calculus, Liu (2008) introduced uncertain differential equation. After that, Chen and Liu (2010) proved the existence and uniqueness theorem for uncertain differential equations. Furthermore, uncertainty theory was also applied to uncertain inference (Liu, 2010a; Gao
As a type of mathematical programming involving uncertain variables, uncertain programming was founded by Liu (2009b). Also, the models of uncertain programming on system reliability design, machine scheduling problem, facility location problem, project scheduling problem, vehicle routing problem and so on, were given by Liu (2009b), respectively. After that, Bhattacharyya
In this section, we introduce some foundational concepts and properties of uncertainty theory, which will be used throughout this paper.
Let Γ be a nonempty set,
Definition 1: (Liu, 2007) An uncertain variable is a measurable function
{ξ ∈B} = {γ ∈Γ | ξ (γ) ∈B}
is an event.
Definition 2: (Liu, 2007) An uncertain variable
Φ(x) = M {γ ∈Γ | ξ (γ) < x}.
Then the inverse function Φ?1 is called the inverse uncertainty distribution of
Example 1: The zigzag uncertain variable
where
Definition 3: (Liu, 2007) Let
provided that at least one of the two integrals is finite.
Theorem 1: (Liu, 2010c)
ξ = f (x1, x2, …,xn)
Example 2: Let
f (x1, x2, x3) = (x1 + x2) / x3
is strictly increasing with respect to
Furthermore, assume the function
We can calculated that the inverse distribution of the zigzag uncertain variable
Also,
Theorem 2: (Liu, 2010c)
In general, a deterministic network is denoted as
Obviously, each
The following example illustrates how to obtain
Example 3: The network
However, in practical, because of the lack of history data, some uncertain factors will appear. In this situation, the weight data can only be obtained from the postman’s empirical estimation. Then how can we deal with this kind of uncertain factor? Fortunately, uncertainty theory provides a new tool to deal with uncertain information, especially subjective estimation.
In this paper, the weights of edges in uncertain network are not precisely known and they are specified as uncertain variables. That is, each weight
[Table 1.] List of notations and assumptions.

List of notations and assumptions.
By the knowledge of graph theory, if network
Thus,
is a route if and only if
Remark 1: If there exists a edge from
Clearly, the shortest route weight in uncertain networkis an uncertain variable. Then, for uncertain network
Expected value is the average value of uncertain variable in the sense of uncertain measure, and represents the size of uncertain variable. Now, we give the concept of expected shortest route for uncertain Chinese postman problem.
Definition 4: Let
a route. Then
is called expected shortest route (ESR) if
Holds for route
where
stands for the total weight of expected shortest route
and
stands for the total weight of route
Furthermore, we give the concepts of
Definition 5: Let
a route. Then
is called
For route
and
is less than
Definition 6: Let
a route. Then
is called distribution shortest route (DSR) if
For route
and for any
For any weight
Then, a key problem is how to get expected shortest route,
In this section, we will construct expected shortest model and
Theorem 3:
where
Proof: According to Definition 4, the expected shortest model can be presented as follows:
Note that,
In fact, the model (2) describes the shortest route in network
Theorem 3 provided a effective method to obtain expected shortest route in uncertain network
Step 1: Calculate
Step 2: Construct a deterministic network
Step 3: Employ Fleury algorithm and Dijkstra algorithm to get the shortest route in uncertain network
The shortest route we get in Step 3 is just the expected shortest route in
Theorem 4:
Proof: According to Definition 5, the
is the optimal solution to the following
Since
Clearly, model (4) is equivalent to
Clearly, model (5) describes the shortest route in network
where
and
Hence the theorem is proved.
Theorem 4 provided a effective method to obtain
Step 1: Calculate
for each weight
Step 2: Construct a deterministic network
Step 3: Employ Fleury algorithm and Dijkstra algorithm to get the shortest route in uncertain network
The shortest route we get in Step 3 is just the
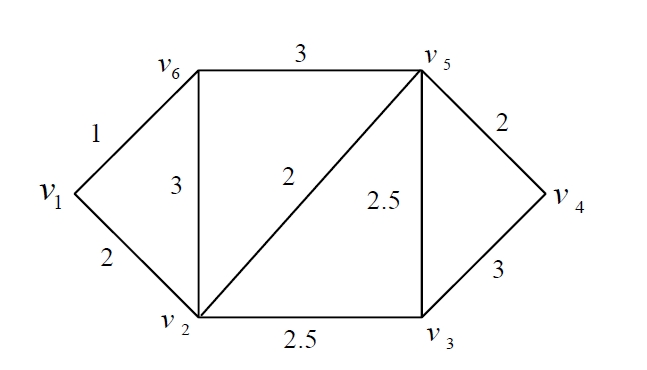
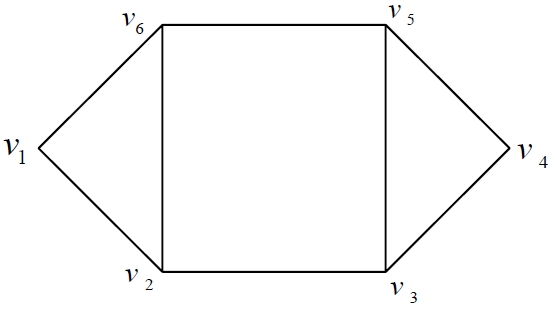
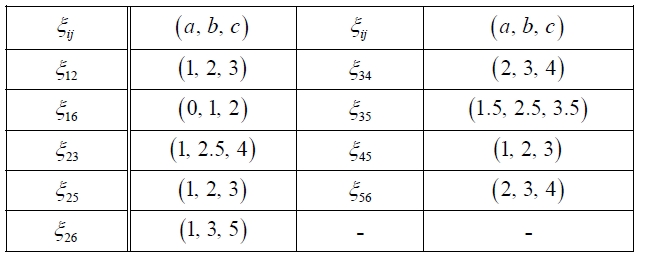
In this section, we give an example to illustrate the methods as mentioned above. We summarize the problem as follows. Suppose that the postman must cover nine streets. Now, the task for the postman is to make the route plan such that the total weight (may be time or expense) on the route is minimized. At the beginning of the task, the postman needs to obtain the basic data, such as traffic condition. In fact, since the plan is made in advance, we usually cannot obtain these data exactly. U-sually, we obtain these uncertain data by means of expert's empirical estimation. Assume that the uncertain network
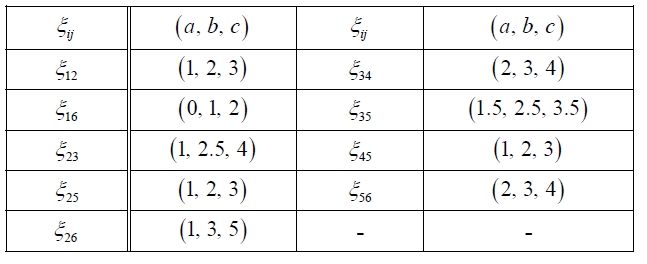
List of ξij.
Step 1: Calculate
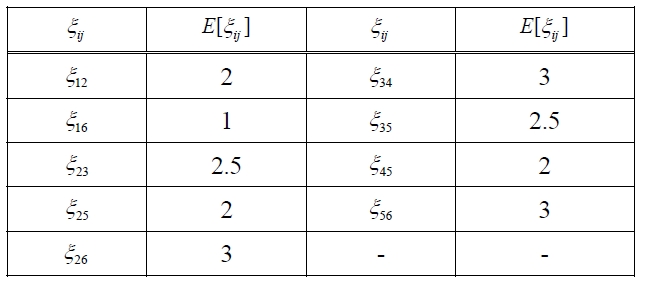
List of E [ξij].
Step 2: From the data in Table 3, we construct a deterministic weighted network is shown in Figure 2.
Step 3: Employ Fleury algorithm and Dijkstra algorithm to the network
According to Theorem 3, the expected shortest route
in uncertain network
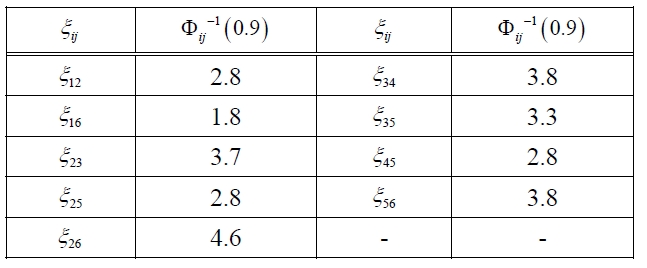
Step 1: Calculate Φ
[Table 4.] List of Φij-1(0.9).
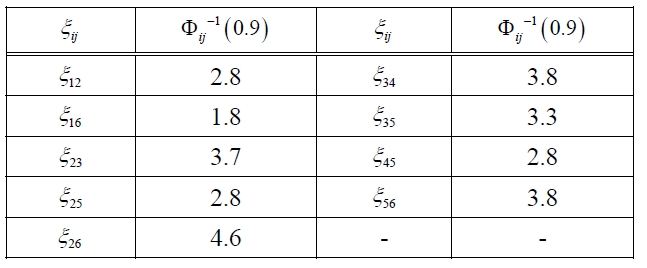
List of Φij-1(0.9).
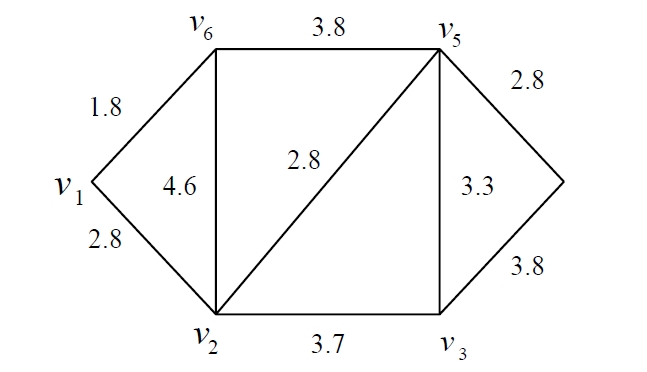
Step 2: From the data in Table 4, we construct a deterministic weighted network is shown in Figure 3.
Step 3: Employ Fleury algorithm and Dijkstra algorithm to the network
According to Theorem 4, the
in uncertain network
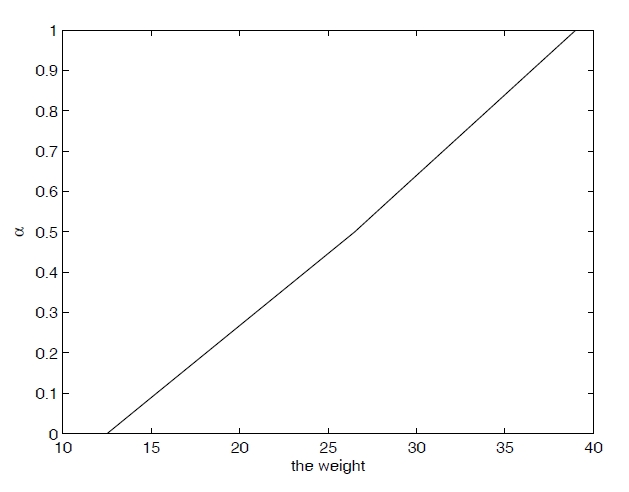
Choosing different
[Table 5.] List of α -shortest route.

List of α -shortest route.
Repeating this process, we can obtain the uncertainty distribution Ψ (
Specially, if the uncertain network
In this paper, the concepts of expected shortest route,
Given an weighted graph
Fleury Algorithm
Step 1: Choose a vertex
Step 2: Suppose that a trail
(i)
(ii) unless there is no alternative,
Step 3: Stop when Step 2 can no longer be implemented.
Fleury algorithm is an efficient algorithm with the complexity
Dijkstra Algorithm
Let
Step 1: Set
Step 2: For any
Step 3: If
Dijkstra algorithm is an efficient algorithm with the complexity

![List of E [ξij].](http://oak.go.kr/repository/journal/11118/SGHHEA_2012_v11n1_18_t003.jpg)