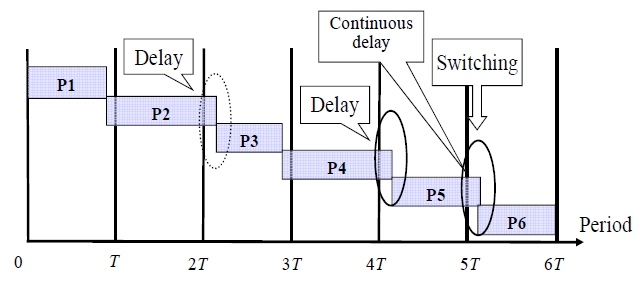
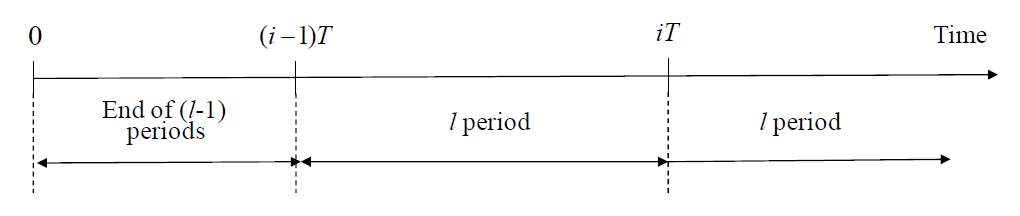
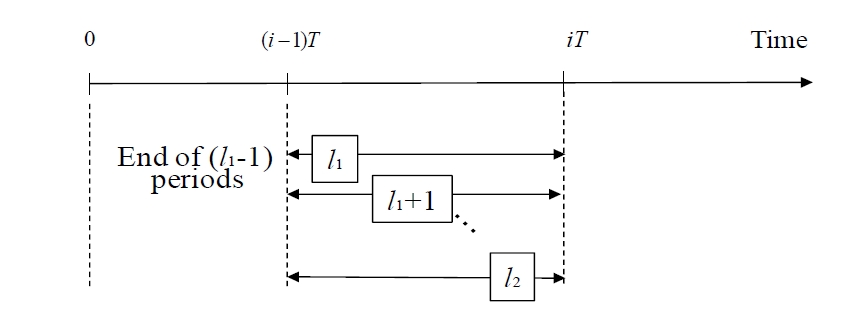
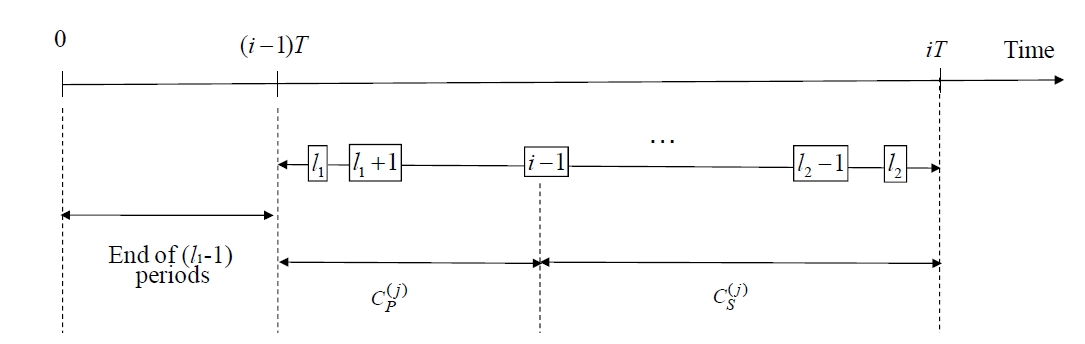
Due to the customer needs of reducing cost and delivery date shorting, prompt change in the production plan became more important.

In the social system or production process of multi periods (or machines or workers) where target processing time exists, idle and delay risks occur repeatedly for multiple periods. In such situations, delay of one process may influence the delivery date of an entire process. In this paper, we discuss the minimum expected cost of the case mentioned above, where the risk depends on the previous situation and occurs repeatedly for multiple periods. There exists an object with some constraints (e.g., due date of production process). These constraints produce a risk and the object occurs repeatedly for multiple periods. This kind of problem is called “a limitedcycle problem with multiple periods” (Yamamoto et al., 2006), and is seen in production lines, time-bucket balancing, production seat systems and so on (Matsui, 2008).

Under the condition of uncertainty, the result or efficiency of a period is often controlled not only by the risks of this period but also by the risks generated beforehand. Whether the process (period or seat) satisfies the due time (restriction) usually depends on the state of the process beforehand, as seen in Wright et al. (1974), Verzijl et al. (1976) and Benders et al. (2002).

In particular, in the case of the risk which depends on a situation of a past process (for instance, the case of a production line for a multi period), how to assign machines, workers or jobs to be most efficient and economical is a problem (optimal assignment) in load/risk planning (for example, see Bergamashi et al., 1997 and Swamidass et al., 2000).

Yamamoto et al. (2006, 2007, 2010a, 2010b) and Sun et al. (2010) considered the optimal arrangement to minimize the total expected cost of such a situation. Before describing a limited-cycle problem with multiple periods, we consider a single limited-cycle problem. If the production time of one period is T and the due time is Z, then the risks due to the length of the production time would occur, which are the risks by T ≤ Z and T > Z. In such situations, it can be noted that there is a trade-off problem in the two risks. This problem is shown as

where β₁ (Z) is the risk by T ≤ Z, and β₂(Z) is the risk by T > Z. This kind of problem is known as various problems of the reliability field, the problem of due time restriction and the newsboy problem (a well-known stock problem) (Week, 1979). A detailed model of a single limited-cycle is shown in Matsui (2005).

This paper considers cases in which the above two risks not only occur in the single period, but also in multiple periods repeatedly. The problem of minimizing the expected cost in such a situation is a limited-cycle problem with multiple periods. The multi period problem could be classified according to whether the periods are independent or not

For this problem, one result is the general form of production rate and waiting time by a station-centered approach as discussed in Matsui el al. (1977) and Matsui (2004). The explicit form is obvious and consists of the product form in the period-independent case, such as a single line, but it is untraceable in the period-dependent case such as a mixed or tandem line. The mixed line has a absorbing barrier, but the tandem line has a reflective barrier at the end. This paper presents a cost approach for the latter.

This paper considers the optimal switching frequency to minimize the total expected cost of the production process. In this paper, first, the optimal switching frequency model is proposed. Next, the mathematic formulation of the total expectation is presented. Finally, the policy of optimal switching frequency is investigated by numerical experiments.

In the production process of multi periods, delay of one process may influence the delivery date of an entire process. We consider controlling the production process by switching the processing rate to a faster one at a given point. The optimal switching problem is when the processing rate should be switched to minimize the total expectation cost. In this paper, we consider the optimal switching point to minimize the total expected cost of the production process. In our considered model, if processing are delay k times continuously, the processing rates should be changed at the next period. Figure 1 shows an example of a switching time model in multiple periods, where period number n is 6 and switching point is 2 (delay continuous times).

The optimal switching frequency model for the multi limited-cycle is considered based on the following assumptions:

(1) One product is made by a process with n processes.

(2) For i = 1, 2,…, n, the production time of process i is denoted by Ti which is assumed to be exponentially distributed and statistically independent, respectively. The usual processing rate is μ1 , and the emergency processing rate is μ2 .

(3) For i = 1, 2,…, n, the target production time of process i is denoted by T, which is set by standard of the process, and the due time of the entire process (n periods) is nT.

(4) k is continuous delay times.

(5) The cost per unit time ( Cs(i) ) occurs when a process is executed before the target production time of the process (i = 1 means before switching and i = 2 means after switching).

(6) The cost per unit time ( Cp(i) ) occurs when a process is executed after the target production time of the process (i = 1 means before switching and i = 2 means after switching).

(7) When

of n periods, the delay cost Cp occurs

(8) When

of n periods, the idle cost Cs occurs.

Some notations are also defined.

For i = 1, 2,…, n,

C (T1, T2, … Tn) : the total cost of the production process.

C(i) : the production cost of period i

Ti : the production time of period i.

Xi : the production time of i periods

Pr(Xn > nT) : the probability of delay.

Pr(Xn ≤ nT) : the probability of idle.

By assumptions mentioned in section 2.1, the object function is set as follows:

where,

E[C(i; T1,T2,…,Ti)] is the expected cost of period i,

C pP r {X n > nT} is the delayed expected cost,

C sP r {X n ≤ nT} is the idle expected cost,

E[C(n+ 1)] is production cost after due time,

and for i =1, 2,…, n

where x _i-1 is the total time from start to period (i-1) ending.

In this paper, for i =1, 2,…, n, the production time of process i is denoted by T_i which is assumed to be exponentially distributed and statistically independent, respectively. The usual processing rate is μ₁ , and the emergency processing rate is μ₂ .

Based on the relation between exponential distribution and Poisson distribution, the terms in equation (1) are given as follows:

For i =1, 2,…, n and t ≥ 0,

Gc (i; t) : The distribution function of total production costs of period i ended on time t, and process doesn’t exceed k times continuously from period 1 to i (before switching).

gc (i; t) : The probability density function of Gc (i; t) .

G (i; t) : The distribution function of total production costs of period i ended on time t, and process doesn’t exceed k times continuously from period 1 to i (after switching).

g (i; t) : The probability density function of G (i; t)

The probability of period i ended on time t, and process doesn’t exceed k times continuously from period 1 to i, and Xi < t

Ge (i; t) : The probability of period i ended on time t, and process exceed k times continuously from period 1 to i, and . Xi < t

He (i,l; t) : The probability of period i ended on time t, process doesn’t exceed k times continuously from period 1 to i-l-1, and period i-l doesn’t exceed, and period i-l-1 to i all exceed.

Theorem 1:

For i =1, 2,…, n,

Theorem 2:

For i =1, 2,…, n, and l =1, 2,…, n,

EC⁽⁰⁾ (i; l) is the expected production cost of l period from (i-1) period to i period under the production process conditions shown in Figure 2.

Theorem 3:

For i =1, 2,…, n

EC_T^(1,2) (i; l₁, l₂, l₁ + k - y - 1) is defined in (iii) of Theorem 4, where l₁ + k - y - 1 is a switching point, and 0 < y ≤ l₁ + k ? n ? 2 .

Theorem 4:

(i) For i =1, 2,…, n, l₁ = i, i + 1,…, n and

l₂ = l₂,l₂+ 1,…, n ( i ≤ l₁, l₁≤ l₂ ),

EC⁽¹⁾ (i; l₁, l₂) is the expected production cost of l period from (i-1) period to i period under the production process conditions shown in Figure 3.

(ii) For i =1, 2,…, n, l₁ = 1, 2,…, n, and

l₂ = l₁,l₁+1 ,…, n (l₁≤l₁),

EC⁽²⁾ (i; l₁, l₂) is the expected production cost of l period from (i-1) period to i period under the production process conditions shown in Figure 4.

(iii) For i =1, 2,…, n - 1, l₁ = 1, 2,…, i - 1,

l₂ = l₁,l₁+1 ,…, n (i > l₁,l₁ ≤ l₂) and

l =1, 2,… l =1, 2,…, k+(l₁-1)(l-(l₁?1)≤k ),

where, for j = 1, 2,

and

Theorem 5:

For i =1, 2,…, n?1, l₁ =1, 2,…, i?1,

In this section, we consider the optimal switching times to minimize the total expected cost by numerical experiments, where μ₂ = 0.3, C_S = 10, μ₁ = 0.1, C_s⁽¹⁾ =4, T=3, C_P⁽¹⁾ = 6, C_s⁽²⁾ = 8, C_P⁽²⁾ = 10, C_P⁽¹⁾ = 20,

We show three cases by production process situations as follows:

(I) Total cost concludes production cost before due time, delay and idle costs.

(II) Total cost concludes production cost (before due time and after due time), delay and idle costs.

(III) Total cost concludes production cost (before due time and after due time).

We can note that (II) is the case of equation (1).

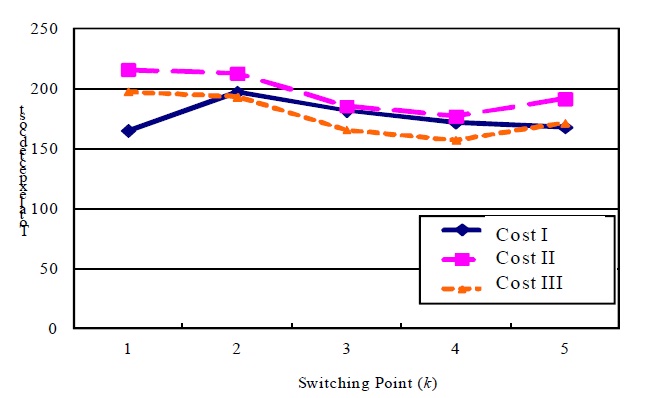
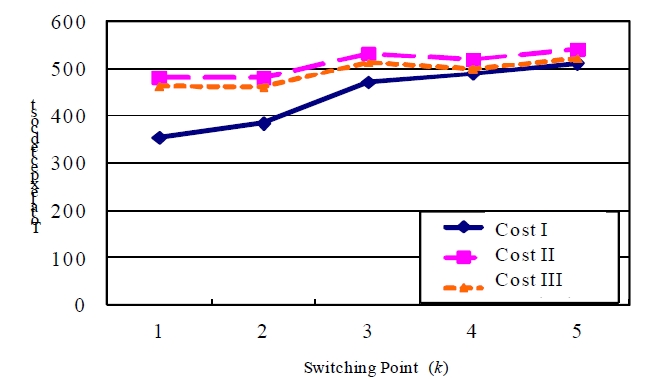
Figure 5 and Figure 6 show the relation of expected costs and switching point k (i.e. continuous delay times).

Figure 5 shows the behavior of the optimal switching point by change of continuous delay times (k) when n = 5. From Figure 5, it can be noted that when cost cases are I, II and III, the optimal switching k are 1, 4 and 4, respectively.

Figure 6 shows the behavior of the optimal switching point by change of continuous delay times (k) when n = 10. From Figure 6, it can be noted that when cost cases are I, II and III, the optimal switching k are 1, 2 and 2, respectively.

From Figure 5 and Figure 6, it also can be noted that optimal switching point k is smaller when the period number n is large. It is means the rate should be switched to a faster one ahead of time when the period number is large. This is because the delay cost could be decreased.

In this paper, we considered the optimal switching point to minimize the total expected cost in limitedcycle problems with multiple periods. First, the optimal switching frequency model is proposed. Next, the mathematic formulation of the total expectation is presented. Finally, the policy of optimal switching frequency is investigated by numerical experiments, and the optimal switching point could be found, too.