It is a common practice to customize processes from reference processes or templates in order to reduce the time and effort required to design and deploy processes on all levels (Lu and Sadiq, 2006). In order to address redundancy and underutilization problems, a generic process model, called as business process (BP) reference, is absolutely necessary to cover the best of process variants. Industrial process model collections and reference process models (e.g., ITIL, SCOR, eTOM) are some related concepts, practices and standards for developing such a process model. However, those concepts are settled as a high-level model without considering the customization implementation. Customization is a major trend that occurs in many industries and markets resulting from the customer’s specific demand on goods and services.
The notion of BP variant is important in explaining the customization in this study. We use the terminology of BP variant to represent the different kind of customized BP with almost similar business objectives. For example, a supplier offers, specifies, produces and delivers different kinds of products to its customers, or suppliers have different kinds of actor relationships that separate orders and frame contracting. Due to the different kinds of BP, there will be a problem in resolving which process is appropriate to a given organization. The difficulty derives from the fact that the activities involved in taking an account to contribute in two or more than hundreds of process. It is certain that a “good” process should be obtained. In order to obtain a “good” process, it is necessary to find a generic process, later called as reference model, that considers a part of sequential view of process with an understanding of the business properties included in the activity.
Approaches to the generation of BP reference models have been explored. Previous work on BP reference model generation has utilized proximity score measurement (PSM) and dealt with activity proximity and frequency as well as validity (Yahya
This study presents a method of solving the multi-objective optimization problem by using forms of genetic algorithms. In multi-objective genetic algorithms we attempt to optimize not only one fitness parameter but also a collection of them. To achieve this, we generate a method of measuring the overall fitness of the set of objectives.
This paper is organized as follows. Section 2 discusses works related to this study. The proposed approach is described in Section 3. The result of experiments is presented in Section 4 and Section 5 concludes this study.
Many efforts have been made on BP modeling research and research on finding reference BP based on BP models is on the increase. van der Aalst
Multi-objective genetic algorithms (MOGA) have been widely used in many areas including order allocation (Wu
In the domain of BP, Quan and Tian (2009) presented a research on business processes’ multi-objective optimization to point out at three criteria of variables: processing time, process cost, and quality. The proposed research used simulation as the result experiments. Vergidis
3.1 Mixed-Integer Linear Programming Model
This section provides definitions of process model and structural schema to describe a formal model of BP.
Definition 1 (Process model).
We define a process model
Ak = {ai| i = 1, …, I} is a set of activities where ai is the i-th activity of pk and I is the total number of activities in pk.
A is defined as a set of all activities in the process repository, where A is the union of all Ak,
Lk ⊆{lij = (ai, aj) | ai, aj ∈Ak } is a set of links where lij is the link between two activities ai and aj in the k-th process. The element (ai, aj) represents the fact that ai immediately precedes aj.
ai+ is the activity following ai and ai- is the activity preceding ai
L is a set of all links in the process repository, where L is the union of all Lk, k = 1, …, K, i.e.,
For a split activity ai, such that |Ni| > 1, where Ni = {aj+ |(ai,ai+)∈L}, f(ai+) = ‘AND’ if all ai+ should be executed; otherwise, f(ai+) = ‘XOR.’
For a merge activity ai, such that |Mi| > 1, where Mi = {aj-|(ai-, ai) ∈ L}, f(ai-) = ‘AND’ if all ai- should be executed; otherwise, f(ai-) = ‘XOR.’
In order to collect information on the variety of start and end activities among process variants, we define AS and AE as the sets of start and end activities, respectively.
AS = {ai| ai ∈ Ak, |Mi| = 0, ∀k ∈ K} is a set of start activities in all K process variants where ai is an activity in pk with an empty set of preceding activities, |Mi| = 0.
AE = {ai| ai ∈ Ak, |Ni| = 0, ∀k ∈ K} is a set of end activities in all K process variants where ai is an activity in pk with an empty set of succeeding activities, |Ni| = 0.
Definition 2 (Structural flow schema).
A structural schema is a set of tuples, each of which has an index and link information. A structural schema (H) required for the chromosome generation is defined as
H = {(s, lij) | s = 1, 2, …, S, and lij ∈ L}
The value of
K : the number of process variants
K : process variant index, k = 1, …, K
S : structural flow schema index, s = 1, …, S
i, j, r, t : activity index
pk : process k in a process repository
Ak : a set of activities in process k
Lk : a set of links in process k
A : a set of all activities in the process repository
AS : a set of start activities among K processes
AE : a set of end activities among K processes
L : a set of all links in the process repository
H : a set of structural flow schema in a group of process variants
Pi : a set of immediately preceding activities (predecessors) of activity i in the process repository
Si : a set of immediately succeeding activities (successors) of activity i in the process repository
Ci : expected cost to execute i-th activity
Cij : proximity score for executing a link (ai, aj) (∈ L)
Ei : expected time to execute i-th activity
Ni : number of predecessors of i-th activity
Mi : number of successors of i-th activity
Vs : coordination time between activities in schemes.
Ws : average coordination time.
(derived from average duration divided by number of links in one structural scheme)
M : big M, a very large positive
ri : ready time for i-th activity
fi : finish time for i-th activity. Particularly, fi = ri+Ei
vi : equals to 1 if activity is selected, ai ∈ A; 0, otherwise
yi : equals to 1 if activity ai ∈ AS is a start activity and an element of the set of start activities; 0, otherwise
zi : equals to 1 if activity ai ∈ AE is an end activity and an element of the set of end activities; 0, otherwise
: equals to 1 if activity ai immediately precedes activity aj in scheme s, (ai, aj) ∈ L, (s, lij) ∈H; 0, otherwise
Note that a tri-objective integer programming model for generating a BP reference model is provided as an extension of a single objective problem. First, it attempts to find the maximum proximity score, (notice that it has been converted into a minimization problem), among the links existing in the process variants. The BP reference should satisfy the business requirements, which are defined as duration (2) and cost (3). Activity duration, called makespan, is a measure to evaluate the expected execution time of a BP reference model. In respect to cost, it will sum the costs of all selected activities for the best BP reference model.
In particular, the constraint can be decomposed into four segments; scheme (4)-(5), predecessors (6)-(9), successors (10)-(13), and predefined duration (14)-(16), respectively. Scheme constraint (4) specifies that a scheme behavioral relation of an activity should be less than or equal to 1. Among all structural schema relations, it should be a scheme that is consistent with (5). With regard to predecessors, constraint (6) expresses that there should be at least one link entering activity
Constraints
Subsequently, with regard to successors, constraint (11) expresses that there should be at least a link leaving activity
Constraints (16)-(19) relate to process duration. Constraint (16) denotes that the ready time of activity
3.2 Multiple-Objective BP Genetic Algorithm
This section proposes a solution to the BP reference selection problem, using a multi-objective genetic algorithm with maximizing proximity score measurement, cost minimization and duration minimization objectives (MOBPGA). MOBPGA considers four parameters, including generation size (
Procedure: Multi-objective business process genetic algorithm (MOBPGA)
begin
initialize P(t);
evaluate P(t) based on the NSGAII;
generate Pareto solutions;
for t = 1 to gen_size do
recombine P(t) to yield O(t) based on the partial- mapped crossover and random key representation mutation;
evaluate O(t) based on the NSGAII;
update Pareto solutions;
select P(t+1) from P(t) and O(t) based on the composite Pareto ranking selection (cPrs);
end
end
The MOBPGA begins with initialization and ends when the number of run generations reaches the generation size. Following several generations of evolution, the algorithms improve solution quality and, in some cases, converge to the optimal solutions of the problem. Increasing the population size, generation size, crossover rate, or mutation rate explores more of the solution space while requiring greater computational effort. The final decision is made by the decision makers, who manually select the preferred Pareto solution according to their preference structures.
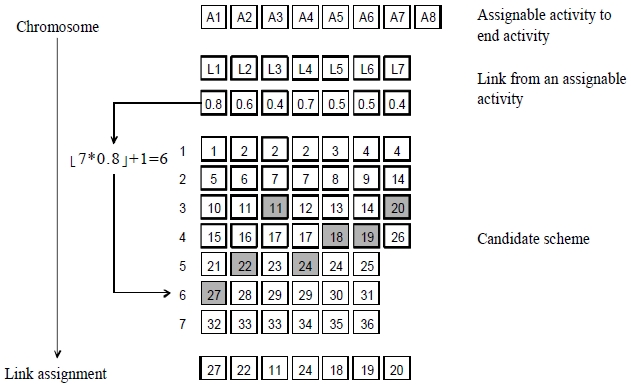
The proposed MOBPGA includes specific random key representation for encoding and decoding, partially mapped crossover, random key representation mutation, an algorithm for efficient Pareto sorting (NSGAII), and composite Pareto ranking selection (cPrs) (Goldberg, 1989). Figure 1 shows the random key representation of encoding method used in this study.
Due to the random genetic processes (crossover and mutation) that might produce an invalid result, it is necessary to verify the process for further generation. We apply the soundness properties of business processes to verify the process well-formedness. For a business process model to be sound, three properties are required (van der Aalst, 2000): 1) for every activity
In order to generate a valid BP, there should be a decoding mechanism that follows some procedures. In this approach, there are three important mechanisms of decoding mechanism for establishing a valid BP. First, it checks the
Step 1: Disqualify schemes flowing to Start of flowing from End.
Step 2: Disqualify pair of activities that are not existed in the repository
Step 3: Disqualify activities that are not available in the path
Step 4: Restructure feasible activities and schemes
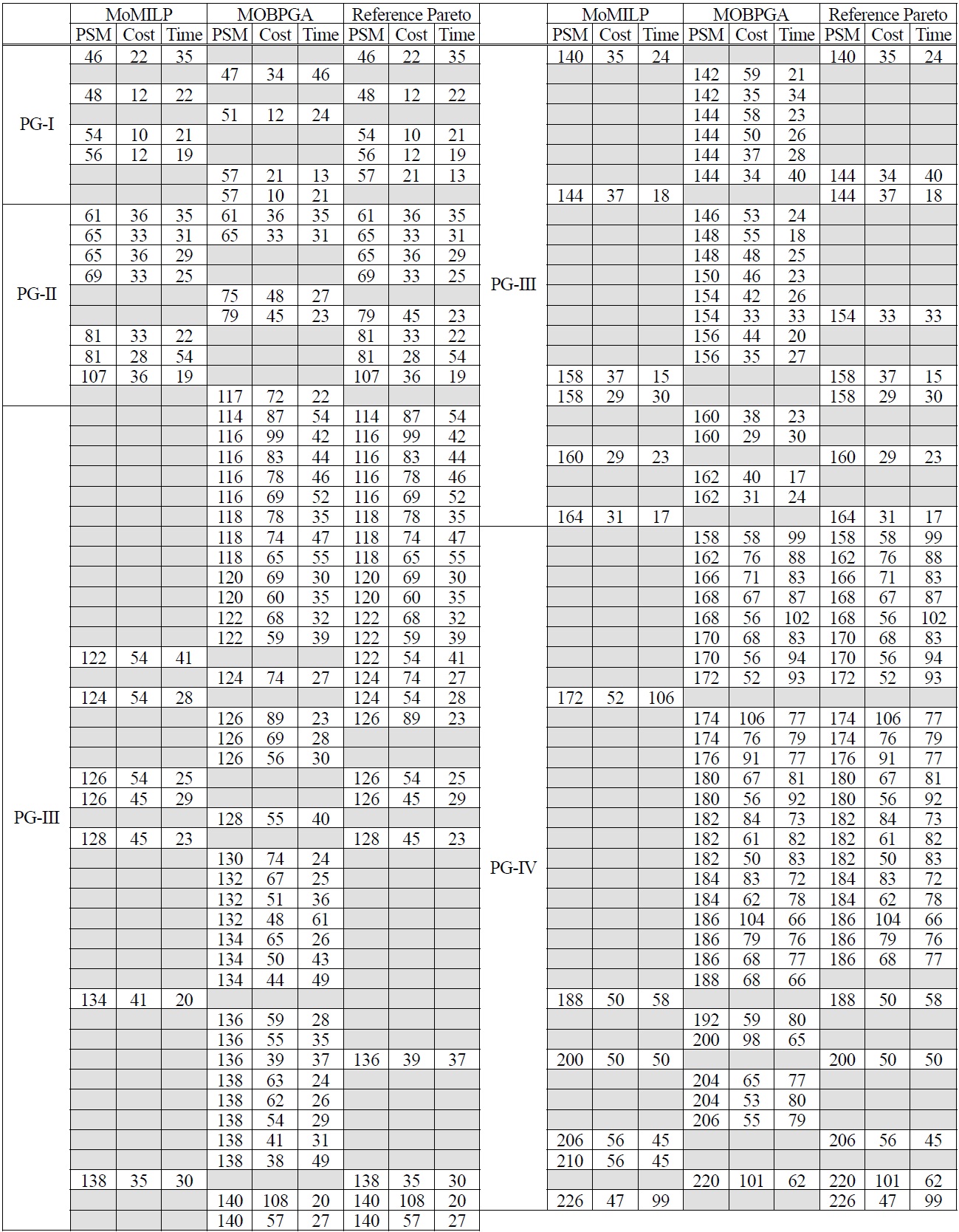
In order to validate our approach, several experiments were conducted. The experiment estimates the validity of the proposed algorithm in real settings by using logistics processes that contain a various types of process structure. Numerical analysis was performed on a desktop computer equipped with an Intel® Pentium® D 3.40GHz CPU and 2GB RAM. The commercial software LINGO 11.0 (LINGO System) was used to generate a reference set of non-dominated solutions, R, utilizing embedded integer programming (IP) packages. For each scenario, LINGO solved the weighted-sums problem with objectives (1)-(3) subject to (4)-(20), which was recognized as ILP (shown in Lingo) and terminated at local optimal solutions. For each problem instance, a local optimal solution was collected within various ranges of computation time. Hence, each scenario has a set of non-dominated solutions for further comparison. The performance metrics discussed above were used to compare the performances of MOBPGA and multi-objective mixed integer linear programming (MoMILP).
We conducted an experiment with various numbers of activities among four process groups (PG). Four groups from PG-I to PG-IV, each consisting of ten process variants (
[Table 1.] Mean number of activities in each group of 4 processes

Mean number of activities in each group of 4 processes
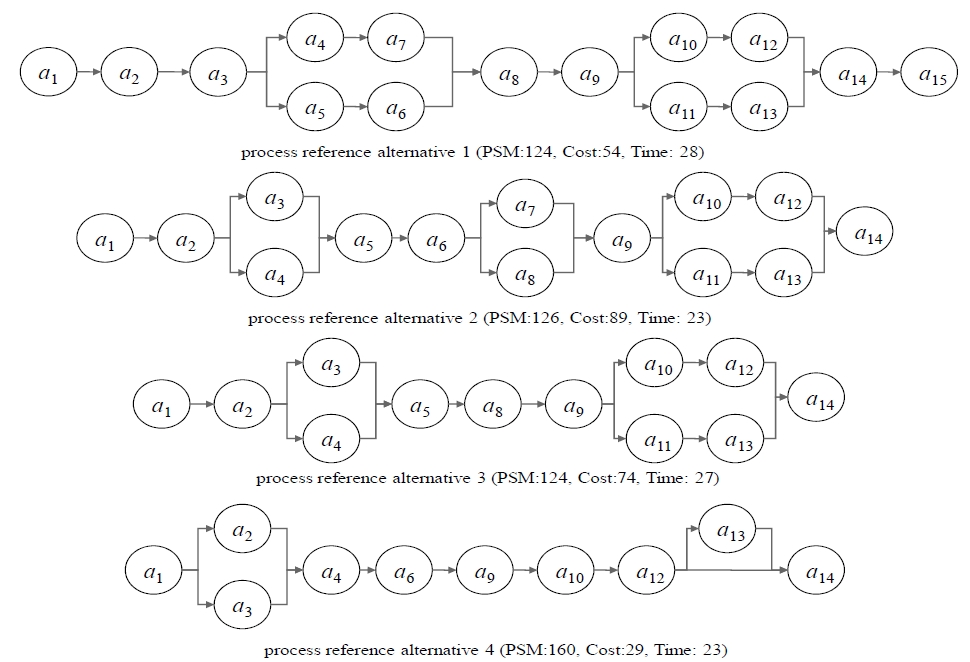
Based on our results using process group III (PG-III), the single-objective approach can produce only a single process reference model, with no guarantee of meeting some requirements (Figure 2). Our proposed approach has several alternatives for decision makers. For example, a process manager might want to select a BP reference model for duration of less than 30 units of time. Some of these alternative candidates are shown in Figure 3. The choice of generating given alternatives will correspond to the stakeholders’ business requirements and will accrue benefits to business organizations in terms of strategic competitiveness.
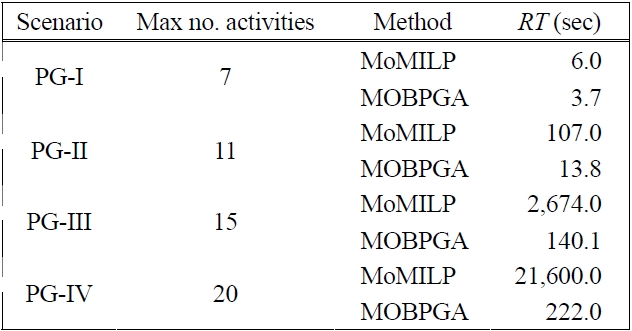
When we applied process variants of activity number 20 (PG-IV), MoMILP computation time was intractable. Thus, we set a cut-off time of 21,600 seconds to obtain feasible solutions. The MOBPGA parameters operative were 1,000 generations, a population size of 20, a mutation rate of 0.8 and multiplier (set on 0.9) for the purpose of selection. Experiment result is shown in Table 2. The computational time of the approaches,
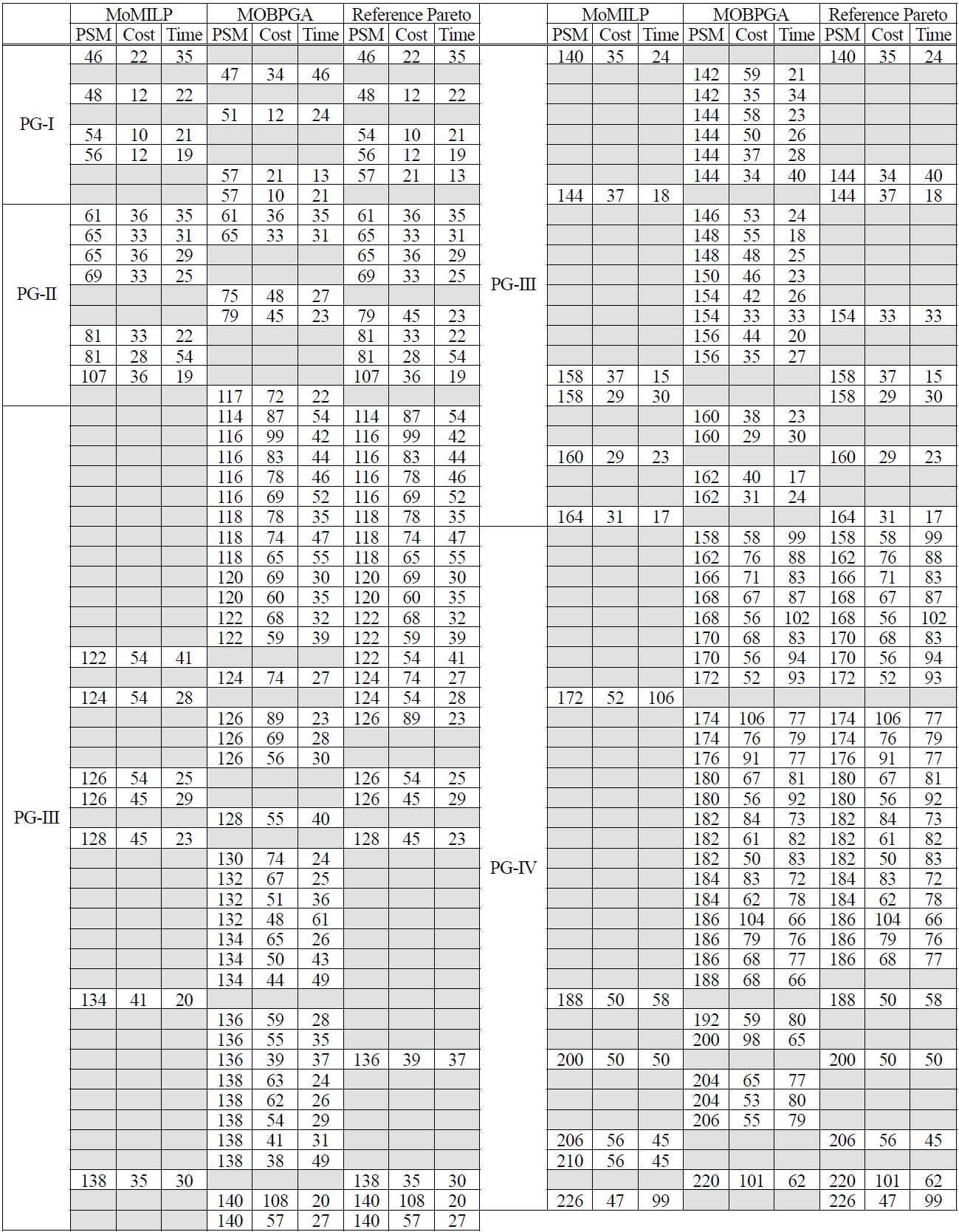
Experiment result
MoMILP and MOBPGA, are listed in Table 3. MoMILP sets a cut-off time of 21,600 seconds for feasible solutions, compared with MOBPGA’s 222 seconds for an activity num-ber of 20. Finally, the performance of the MOBPGA is robust and our performance evaluations showed little dif-ference from MoMILP in terms of quality of the solutions.
[Table 3.] Performance evaluations of three scenarios using MoMILP and MOBPGA
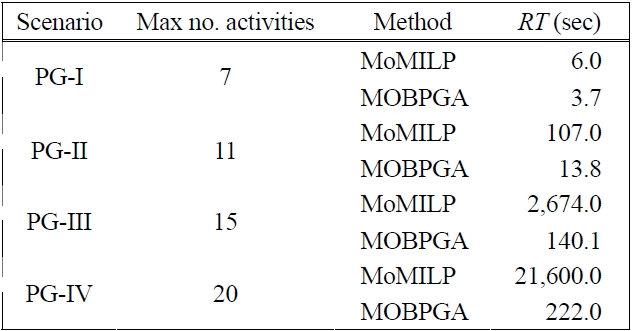
Performance evaluations of three scenarios using MoMILP and MOBPGA
This paper proposes a MOBPGA with specific random key representation of encoding and decoding to solve the problem of BP reference model generation with objective functions maximizing process proximity while minimizing cost and duration. The proposed model meets customer requirements by coordinating objectives, specifically by incorporating the process topology into the operational objectives. It also presents a compromise approach that can facilitate decision making in the context of a large set of Pareto solutions, thereby enabling decision makers to incorporate other preferences or business concerns. By utilizing the results of non-dominated solutions both from MOBPGA and MoMILP, we can suggest alternative solutions to stakeholders based on certain conditions. Compared with the conventional ap-proach, this provides more solutions to decision makers, enabling them to select process reference models based on their requirements.
BP reference model generation will have to be improved, considering the following limitations. First, this study employed experiments using the block concept of process structure. Whereas there are some benefits on the experiments, this approach covers a little issue with regard to deadlock and flawless process in BP. Moreover, there are some issues remaining with regard to operation dependency within activities. Second, since the graph generation was assumed to be flawless, there is a need to carefully consider the control flow semantics such as AND or OR control-flow in generating the BP reference model. These are issues that will require further research.