Let V and W be two sets of separated points in the plane, specifically, the black points and the white points, respectively. If |V| = n and |W| = m, then the average distance between V and W, denoted by μ(V,W), is defined to be the average distance of p and q for all point pairs (p,q) ∈ V × W:

wher e d(p,q) denotes the distance of p and q in the plane, in particular, we will only consider the L¹-distance of the plane in this paper.

In this paper, we consider the case in which V and W are completely separated by a wall. This is inspired by the situation where the Palestinian area and the Israeli area are separated by a wall. We cannot go through the wall from a black point to a white point. Thus we wish to make a gate in the wall in order to connect black points and white points. Then, to go from a black point to a white point, we should go from the black point to the gate and then from the gate to the white point. Therefore, for agate g, the distance d(p,q) between a black point p and a white point q in this environment is given by

In this paper, we will investigate a location problem in this environment, which is about where to make a gate in the wall. In particular, we are concerned in locating the gate to minimize the average distance between V and W, which means constructing the gate to make mutual visits between the two separated areas easy.

This is closely related to the well-known facility location problem, in which a company wants to open up a number of facilities to serve their customers. In the problem, both the opening of a facility at a specific location and the service of a customer by a facility incurs some cost. The goal is to minimize the overall cost of opening enough facilities to serve all the customers.

There are four primary problems in facility location: the p-median problem, the p-center problem, the uncapacitated facility locationproblem (UFLP) and the quadratic assignment problem (QAP). These problems are specific variants of the general facility location problem.

Our problem may be considered one of a number of variants of the facility location problem. It corresponds to the case in which there is no cost to open a facility, say a gate, and the service costs are the distances between the pairs of black and white points.

In this paper, we will obtain an efficient algorithm to find a gate in the wall minimizing the average distance between black points and white points.

The problem of determining the average distance is mostly concentrated on the graph. One method of computing the average distance of a graph with n nodes is simply to compute the distances between all pairs of vertices, which is performed in time O(n²). In [1], the author asked whether the average distance of a graph is easier to compute than all distances between vertices of the graph. An affirmative answer is given in [2], which presents an algorithm that computes the average distance of an interval graph with m edges of unit weight in time O(m). The author provides an algorithm that computes the average distance of a tree with n nodes and p edges in time O(n).

Our problem is related to variants of the facility location problem in the Euclidean space: the median problem and the center problem. In the median problem, the sum of distances from the clients to their nearest facilities is minimized, whereas the maximum distance between the clients and their nearest facilities is minimized in the center problem.

For the 1-median problem, it is well-known that there is a linear time algorithm in R. But solving for the exact location of the Euclidean 1-median in two or more dimensions is difficult in general. Indeed, no polynomial-time algorithm is known, nor has the problem been shown to be non-deterministic polynomial-time hard (NP-hard) [3]. There is a randomized algorithm with its running time linear in n and polynomial in 1/e [4, 5].

For an arbitrary p, in R, the p-median can be solved exactly in O(pn) time [6]. However, it is NP-hard even inR²[7]. Arora et al. [8] provide an O(n^(O(1+1/e)))-time e-approximation algorithm.

In the case of the 1-center problem, there is a deterministic O(n)-time algorithm in R² [9]. This result has been extended to R^d for any fixed d in O(d^(O(d))n) time by [10, 11]. The 2-center problem has been solved by a number of works [12-17]. The best recentsolution is an O(nlog² nlog² logn)-time algorithm given in [18]. Agarwal and Sharir [19] provide a generalization of Drezner’s algorithm from R² to R^d to give an algorithm requiring O(n^d+1) time.

The Euclidean k-center problem can be solved in linear time in R using the algorithm of [20] for finding the k-centers in a tree. The problem is shown to be NP-hard in R² [7]. There are many approximation algorithms for the Euclidean k-center problem [21-24].

The problem that we will deal with is one of various variants of the facility location problem and it is first investigated in this paper. We will propose an efficient algorithm running in linear time.

Let V and W be the sets of black points and white points, respectively, where |V| = n and |W| = m. There is a wall located between V and W and dividing the black points and the white points.

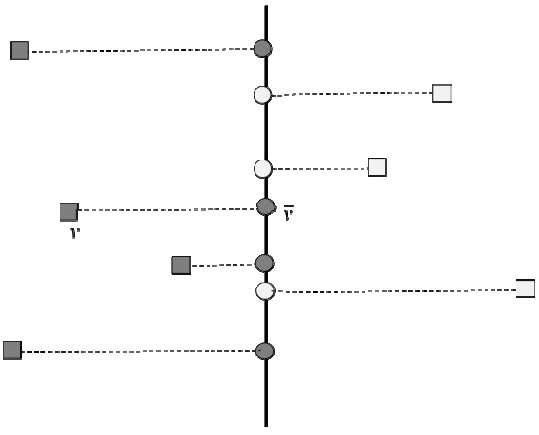
We consider a gate g, a point lying on the wall. Then the distance d(p,q) between p ∈ V and q ∈ W is given as d(p,q) = d(p,g) + d(g,q). To compute the distance easily, we will apply the projections of points in V ∪ W onto the wall as shown in Fig. 1. Let v be a point in V ∪ W. Then the projection of v onto the wall is denoted by

Thus the distance from v to the gate g can be given by

Here both the point

and the gate g are located on the wall. Also note that

is uniquely determined regardless of the location of the gate g.

For p ∈ V and q ∈ W, the distance d (p,q) is given as

Thus, for any black point p ∈ V, the sum of distances between it and all white points q ∈ W is obtained by

Thus the sum of distances of all pairs of p ∈ V and q ∈ W is

Let

and O =

Then both P and Q are fixedly determined. Therefore, the goal is transformed to minimizing the function O. That is, we derive a one-dimensional equivalent problem that finds a gate g to minimize the function O for (n + m) points given on the line. From this point on, we will solve the equivalent problem.

Given points

on the line where |V|=nand |W|=m, we want to obtain a (gate) point g that minimizes the objective function O given by

Here, we will provide an algorithm A to solve the above problem. We consider the points

as points p_i with weights w_i on the line. If p_i ∈ V, then

If p_i ∈ W, then

Then the objective O'=∑_iw_i d(p_i,g) is the same as

Thus the optimal solution g also minimizes O'. We will show that the weighted median of points p_i minimizes the objective O'.

The weighted median of points p_i is defined to be p_k, one of the points satisfying

where ∑_iW_i =1.

Thus we consider an algorithm A to find the weighted median of points p_i. In A, first sort the points p_i in non-decreasing order. Then sum up the weights of points until we have found the median, that is, until the sum is more than or equal to

Thus A is run in O(n log n) time.

Given the validity of the algorithm A, it remains to prove that the weighted median of points minimizes the objective O'. The next theorem shows that.

Theorem 1: Given points p_i with weights w_i on a line, where ∑_iw_i =1, for the weighted median μ of the points, the objective function ∑_iw_i d(p_i ,p) is minimized when p=μ.

Proof: First, sort the points p_i in non-decreasing order. Then let the weighted median μ be the point p_k. Assume to the contrary that the point p minimizing the objective function is not p_k. Then we should consider two cases:

because the points p_i are sorted in non-decreasing order. Then we also obtain the following inequalities:

Then we consider L₁-Land L₂-L. We can show the terms are both non-negative as follows:

because from the definition of the weighted median,

Consequently, we show that L₁ ≥ L and L₂ ≥ L. This completes the proof.

Corollary 1: Let V and W be the sets of black points and white points, respectively, divided by a wall, where |V| = nand |W| = m. There is an O((n + m) log(n + m))-time algorithm to find a gate minimizing the average distance between V and W for the L¹-distance of the plane.

In this paper, we consider a variant of the facility problem in a plane. Given separated points divided by a wall, we find a gate locationon the wall to minimize the average distances between the points in L¹-distance. An O(n log?n)-time algorithm is provided, where n is the total number of points.

For further work, we may considervarious objective functions, for example, the longest distance between points, called by the diameter. Also the problem in which the number of gates is more than one is interesting.