



Spread spectrum (SS)-based watermarking is one of the most representative method of the blind additive embedding (AE) model, which relies on the theory of spread spectrum communication for information embedding and detection. More specifically, in case of SS-based watermarking, the host signal acts as interference at the blind detector (the host signal, x, is not used during the watermark detection process) and because the host signal has much higher energy than the watermark, host interference causes the detection performance to deteriorate at the blind detector (or detectors, hereon unless otherwise stated). Superior detection performance is one of the desirable features of the blind AE model.
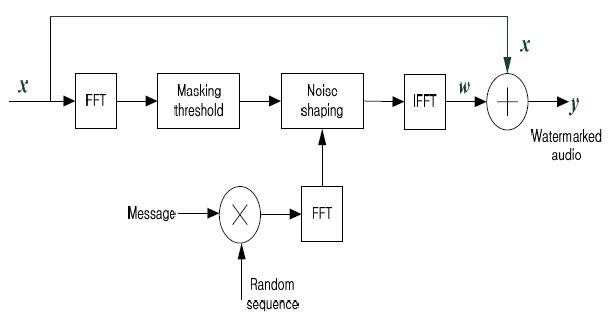
The main motivation of this paper is to design a blind detector for SS-based watermarking. Existing detectors for SS-based watermarking schemes are bounded by the host signal interference at the detector. The proposed detector intends to reduce the host signal interference by developing an estimation-correlation-based detection framework. The proposed detector, therefore, consists of two stages: 1) watermark estimation stage, and 2) watermark detection stage. The objective of the watermark estimation stage is to estimate the embedded watermark, which has a higher watermark-to-signal-ratio (WSR) than the watermarked audio. To accomplish this goal, blind source separation based on the underdetermined independent component analysis (UICA) framework (i.e., ICA for more sources than sensors) is used for watermark estimation. To this end, we model the problem of blind watermark detection for AE as that of blind source separation (BSS) for underdetermined mixtures. To ensure better WSR at the watermark estimation stage, the watermarked audio is pre-processed to remove correlation in audio signal using linear predictive (LP) filtering. It has been shown that the received watermarked signal is an underdetermined linear mixture of the underlying independent sources obeying non-Gaussian distributions, therefore BSS based on the UICA framework can be used for watermark estimation [1].
A similarity measure based on correlation is then used to detect the presence or the absence of the embedded watermark in the estimated watermark. Performance of the proposed watermark detection scheme is evaluated using a sound quality assessment material (SQAM) downloaded from [2]. Simulation results for the SQAM dataset show that the proposed scheme performs significantly better than existing estimation-correlation-based detection schemes [2] based on median filtering and Wiener filtering.
The majority of existing SS-based watermarking schemes [3] use an AE model to insert the watermark into the host audio. Mathematically, the SS-based watermark embedding process can be expressed as
where
respectively. It is assumed further that
Adversary attacks or distortion due to signal manipulations,
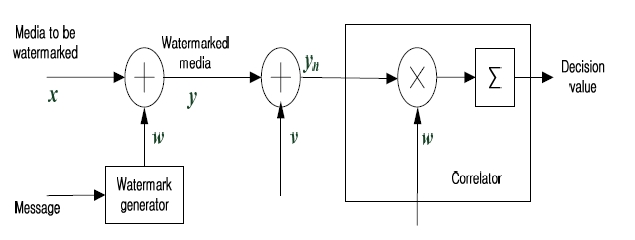
is processed at the detector to detect the presence or the absence of the embedded watermark. The basic additive embedding and correlation based detection framework is shown in Fig. 1.
A correlation-based detector is commonly used to detect the presence or the absence of the embedded watermark. The decision threshold,
where
is the energy of the watermark, E
It is important to mention that detection performance of the correlation-based detector depends on the decision threshold used. Let us assume that watermark detection threshold
where
It can be summarized that the detection performance of a blind detector for additive watermarking schemes is inherently bounded by the host-signal interference at the detector. The motivation behind this paper is to design a watermark detector for AE with improved watermark detection performance. Towards this end, the proposed detector uses the theory of ICA by posing watermark estimation as a BSS problem from an underdetermined mixture of independent sources. The fundamentals of the ICA theory are briefly outlined in the following section followed by the details of the proposed ICA-based detector.
>
A. Independent Component Analysis
ICA is a statistical framework for estimating underlying hidden factors or components of multivariate statistical data. In the ICA model, the data variables are assumed to be linear or nonlinear mixtures of some unknown latent variables, and the mixing system is also unknown [4]. Moreover, these hidden variables are assumed to be non-Gaussian and mutually independent. The linear-statistical, static ICA generative model considered in this paper, which is given as
where
The mixtures in which the number of observations(dimensionality of observation vector,
Before BSS based on underdetermined ICA can be used to estimate the watermark from the watermarked audio, we need to verify the following: 1) the watermarked audio is an underdetermined mixture of independent sources, and 2) the underlying sources obey a non-Gaussian distribution. It can be observed from Eq. (1) that the AE model fits into an underdetermined linear mixture model; therefore, BSS for underdetermined mixtures can be used to estimate the embedded watermark given that the underlying latent sources (
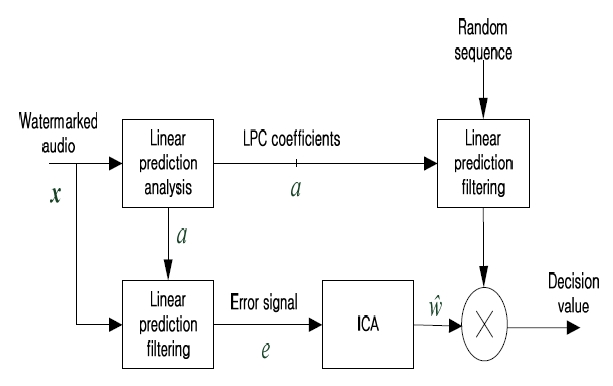
This section provides an overview of the proposed blind watermark detection scheme from the received watermarked audio signal obtained by additive embedding. The proposed watermark detection scheme consists of two stages: 1) the watermark estimation stage, and 2) the watermark detection stage. It was mentioned earlier that the watermark estimation stage is further divided into two sub-stages: the spectral removal stage and the source separation stage.
The goal of the watermark embedder is that the embedded watermark should survive intentional and unintentional attacks, whereas the goal of the watermark detector is to detect the embedded watermark with very low false rates in the presence of an active adversary and signal manipulations. In case of the AE model, low false rates are difficult to achieve due to strong host interference. For detector performance analysis, existing correlation-based schemes model the audio signal as a white Gaussian channel. Recent results in audio processing and compression community, however, show that samples of the real audio signals are highly correlated, which can be exploited to improve the detection performance by de-correlating the input audio before detection. The proposed detection scheme achieves this goal by applying whitening or de-correlation before watermark estimation. Simulation results presented in this paper show that the whitening before watermark estimation using ICA improves detection performance significantly. This improvement can be attributed to the fact that whitening actually increases the watermark to interference ratio and hence yields superior detection performance.
To remove the correlation in the audio signal, an autoregressive modeling named linear predictive coding (LPC) [7] can be used. The LPC method approximates the original audio signal,
where the coefficients
where
Likewise, watermark audio can also be expressed as,
where
is the residual signal of the watermarked audio signal. We assume that, by the characteristics of linear predictive analysis,
has the characteristics of both
defined as
Here prediction error,
It can be observed from Eq. (11) that the estimate
with the audio spectrum removed has the characteristics of both the excitation signal of the original audio
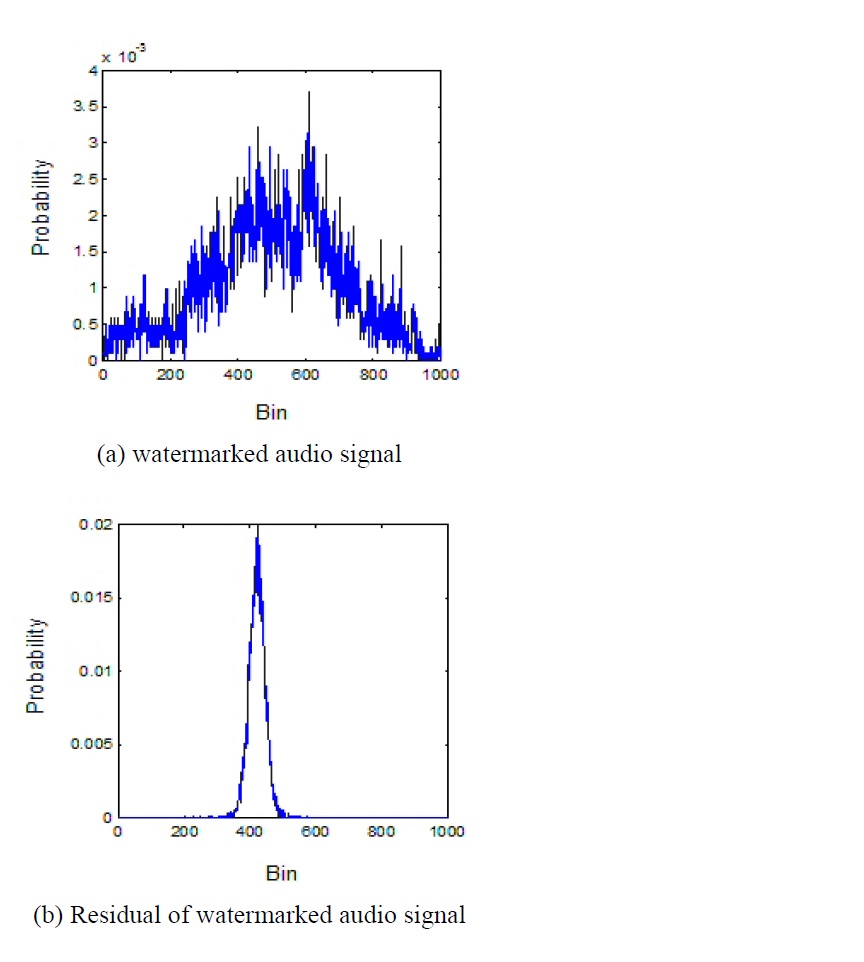
This method transforms the non-white watermarked audio signal to a whitened signal by removing the audio spectrum. It can be observed from Fig. 2 that is the empirical probability density function (pdf) of a small segment of the watermarked audio signal before LP filtering and the residual or error signal of the watermarked audio signal after LP filtering. The empirical pdf of the watermarked audio signal is clearly not smooth and has large variations due to the voiced part. On the other hand, the empirical pdf of the residual signal has a smoother distribution and a smaller variance than the watermarked audio signal.
It is important to mention that the LPC stage also improves WSR which ultimately improves the source separation performance of the BSS used for watermark estimation. This is because, the watermark sequence is i.i.d., so the de-correlation stage does not reduce its energy in the residual signal, whereas, de-correlation does reduce audio signal energy.
The residual signal is the then used to estimate the hidden watermark using BSS based on UICA. For watermark estimation, the probabilistic ICA method based on mean-field approaches is used. Superior source separation performance is the only motivation behind using of the probabilistic ICA presented in [1]. This is, however, not the limitation of the proposed scheme, as any of the BSS schemes based on UICA can be used for watermark estimation from the residual signal. Estimated sources are then correlated with the watermark,
The binary message to be embedded is first modulated by a key-dependent random sequence. The watermark is then spectrally shaped in the frequency domain according to a masking threshold estimated based on the human auditory system (HAS) ISO/MPEG-1 Audio Layer III model [8]. The motivation here is to design the weighting function that maximizes the energy of the embedded watermark subject to a required acceptable distortion. The resulting watermark is then added into the original audio signal in the frequency domain, which is then transformed to the time domain to obtain the watermarked audio. A semantic diagram of the audio watermark embedding scheme discussed above is shown in Fig. 4.
The simulation results presented in this section are based on the following system settings: 1) 44 kHz sampled and 16-bit resolution audio signals are used as the host audio, 2) a 1,024-point watermark is then embedded into four consecutive non-overlapping frames, 3) the watermarked signal is first segmented into non-overlapping frames of 4,096 samples each, then each frame is further segmented into four non-overlapping sub-frames which are then applied to the ICA block to estimate the embedded watermark after LPC filtering. For performance evaluation, SQAM downloaded from [2] was used.
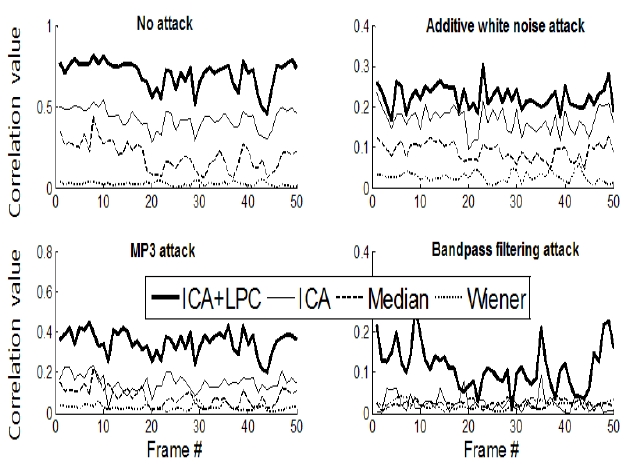
The robustness performance of the proposed the proposed watermark estimation scheme was evaluated for the following attack scenarios: 1) no adversary attack, 2) additive white Gaussian noise, 3) MP3 compression (128 kbps), and 4) bandpass filtering (2nd-order Butterworth filter with cutoff frequencies 100 and 6,000 Hz).
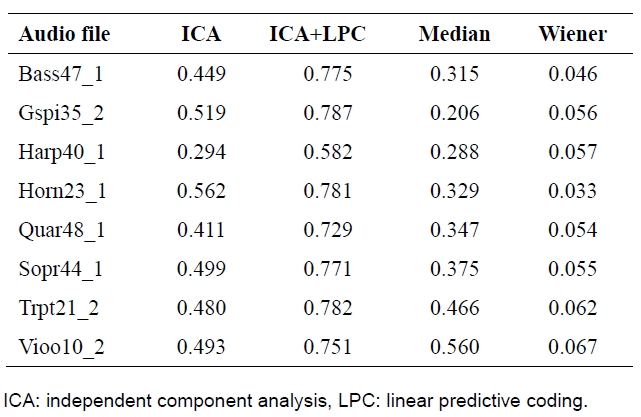
Correlation values depending on the detection method using the sound quality assessment material [2] database for magnetic propertie
Detection performance of the proposed estimation-correlation based detector scheme and the existing schemes for these attacks is given in Fig 5. It is observed from Fig. 5 that, for four attack scenarios, the proposed detector outperforms the exiting detectors. In addition, detection performance of the watermark detectors under consideration for the SQAM database is given in Table 1. It can be observed from both Fig. 5 and Table 1 that the proposed detector performs significantly better than its counterparts. Improved detection performance of the proposed detector can be attributed to its better host signal interference cancelation capability.
In this paper, we described a new framework for estimation-correlation based detection for additive embedding. The proposed blind detection method extracts the embedded watermark signal suppressing the host signal interference at the detector. The proposed framework exploits mutual independence and non-Gaussianity of the audio signal and the embedded watermark to estimate the embedded watermark using BSS-based UICA. Experimental results showed that the proposed detection scheme is robust.
![Correlation values depending on the detection method using the sound quality assessment material [2] database for magnetic propertie](http://oak.go.kr/repository/journal/11020/E1ICAW_2012_v10n2_175_t001.jpg)