Many natural and man-made systems are structured in the form of graphs. Typical examples include communication networks,biological systems, social networks and transportation infrastructures. The increasing popularity of these graph data has initiated a fertile research area in information extraction and data mining that benefits various application fields such as sociology,marketing, biomedicine and counterterrorism. However,as more real world graph data have been made publicly available,the privacy preservation, which already has a rich body of research on transactional data [1-4], becomes an important concern associated with graph analysis. In this paper, we focus on protecting sensitive identities of individuals in a graph from background knowledge attacks. That is, if certain local knowledge can uniquely identify some vertices in a graph and is known by an adversary, the privacy of these entities can be breached, even if the data has been perturbed before publication.

Some recent studies [5, 6] show that the simple technique of anonymizing graphs by removing the identities/labels of vertices before publishing the actual graph does not always guarantee privacy. For example, the work in study of Zhou and Pei [7]identifies neighborhood attacks that an adversary has knowledge about neighbors of a target vertex and the relationship among the neighbors. Another study [8] discusses a specific knowledge attack, assuming an adversary has prior knowledge of the degree of a target vertex. They argue that, if the degree of a vertex is unique in the degree sequence of all vertices, this entity can be easily re-identified, even without its original label.

A common character of the studies mentioned above is that they all concentrate on simple graphs (i.e., undirected, unweighted

[Fig. 1.] Examples of degree anonymized weighted graph.

and loopless graphs) and avoid weighted networks that are often perceived as being harder to analyze than their unweighted counterparts are. However, as has long been appreciated, many networks are intrinsically weighted, their edges having differing strengths. There may be stronger or weaker social ties between individuals in a social network. There may be longer or shorter distances between stations in a transportation network. There may be more or less bandwidth or data flow between routers/clients in a communication network. There may be more or less flux along particular reaction pathways in a metabolic network.There may be more or less energy or carbon flow between predator-prey pairs in a food web.

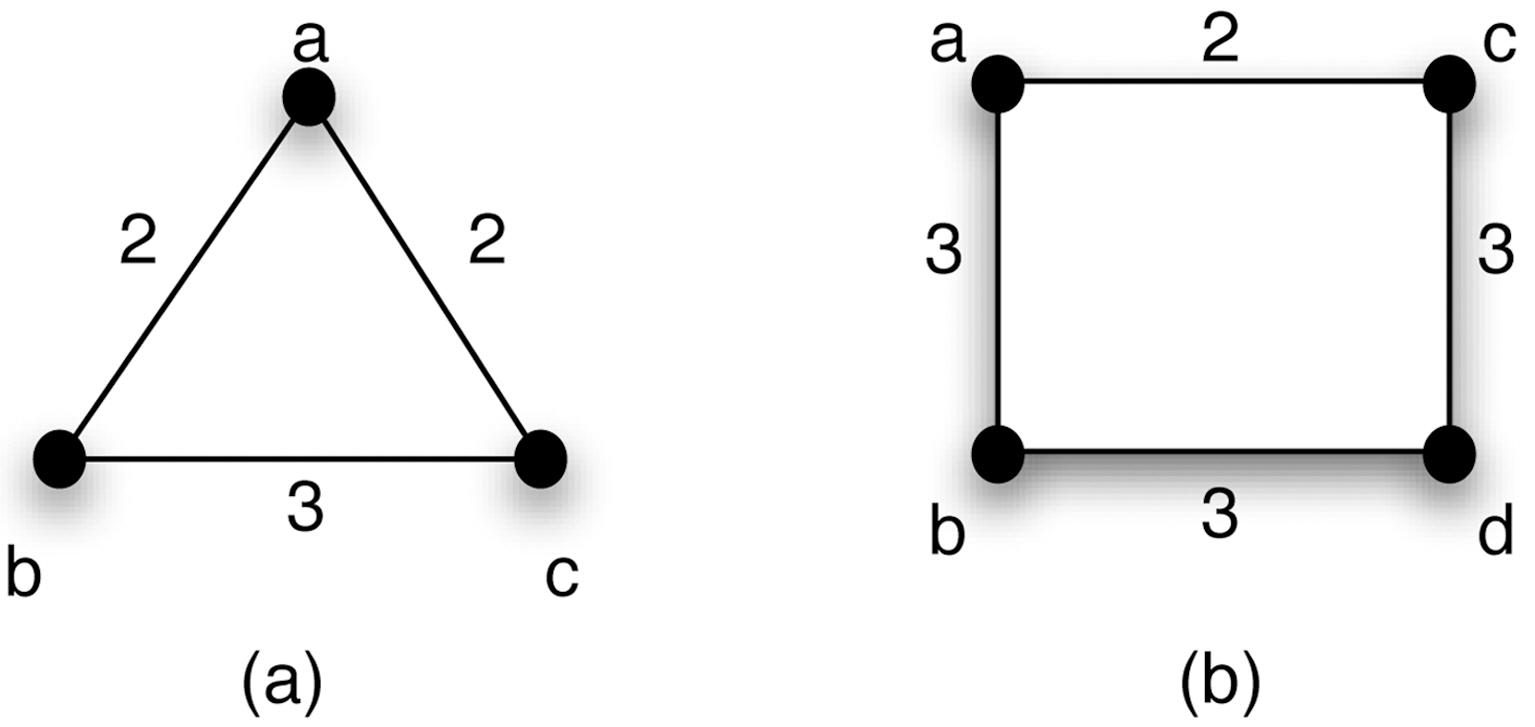
In this paper, we discuss weighted-related properties that may lead to potential background knowledge attacks in a graph.Two important properties are introduced here: 1) volume, which is sum of weights for a node; and 2) histogram, which represents the neighborhood weight distribution of a node. From both theoretical and practical views, a weighted graph provides more unique structural information than a simple graph that increases the risk of identity disclosure. For example, a realworld graph, called NetSci, which has 1; 589 nodes and will be introduced in the experimental section, consists of 1% nodes with unique degree values but more than 6% with unique volume values. We will show the details in the experimental part.Furthermore, many preservation algorithms for simple graphs may not be extended or adapted to their weighted version. For instance, Fig. 1 states two weighted graphs, which are 3-degree anonymous and 4-degree anonymous respectively, according to the definition in [8]. However the weight values provide some extra unique information for a vertex, e.g., the volume of the vertex a is unique in Fig. 1a. In the real world, such information may be known as background knowledge and used by adversaries for re-identification.

While the privacy preservation has the highest priority in our discussion, we also consider another aspect, which is to maintain the so-called community in graphs. In societies, a community can be a variety of group organizations, such as families,friendship circles or colleagues. In online social networks, a community can be a virtual interest group. In protein-protein interaction networks, a community can be a group of proteins having the same specific function within a cell. As one of the major features of graphs representing real systems is community structure [9], detecting such communities is of great importance in various disciplines, such as sociology, biology and computer science. This is usually known as community detection in the graph clustering area, and has been a vibrant research field for the last few years [10-14]. Therefore, it is either necessary or practicable to ensure a privacy preservation approach to maintain the community structure of a published dataset.

- We discuss the identity disclosure problems in weighted graphs with certain weight properties as background knowledge.Two weight characteristics are considered: 1) volume:the sum of weights for a vertex; and 2) histogram: the neighborhood weight distribution of a vertex, and we show empirically how high the disclosure risk is with these weight attacks to breach real-world graphs.

- We formalize a general model for weighted graph anonymization,which is to modify edges and weights in a graph to prevent weight-related attacking.

- We provide a complete solution for the weight anonymization problem introduced in this paper, and show theoretically and empirically how the proposed methods perform on both data privacy and utility.

- We consider the change of graph spectrum as information loss incurred in graph perturbation, and use the algebraic connectivity as a quantitative metric.

- We also theoretically justify the impact of weight modification on the graph spectrum.

- We explore the impact of the proposed approaches on community detection that is a concrete and popular application in the field of graph mining and analysis.

The remainder of this paper is organized as follows. Section II brief overviews the literature on the graph anonymization problem. In Section III, we formally define a general model for weighted graph anonymization and provide two concrete cases of weight-related attacks. We also discuss the use of a graph spectrum as the information loss during anonymization in this part. Section IV focuses on methods against both weight attacks. We present the experimental results in Section V. In Section VI, we explore the issue of community detection with graph anonymization. We conclude this paper in Section VII.

In recent years, a large number of techniques, such as data swapping [15], microaggregation [2], and k-anonymization [4,16, 17], have been proposed for the identity disclosure problem in relational databases. Most of these fundamental studies are group-based that means the approaches will partition data according to a certain metric and generalize/suppress data tuples in each group. An extensive study can be found in [18].

Hay et al. [5] point out the risk that simply removing the identifiers (or label) of the nodes does not always guarantee privacy.They study a spectrum of adversary external information and its power to re-identify individuals in a social network. Two types of adversary knowledge are formalized in detail: 1) vertex refinement queries that reveal the structure of a graph around a vertex. For a node v, such information includes its label, degree,the list of its neighbors’ degree, and so on. 2) subgraph knowledge queries, which investigate the uniqueness of a subgraph around the target node. The above two directions are also extended by the following studies [7, 8] that we will describe in the following part. The paper also provides a solution to anonymize the social network data based on random perturbation.

The work in [6] describes a family of attacks on a social network whose labels for vertices are replaced with meaningless unique identifiers. The idea behind these attacks is to create or find unique subgraphs embedded in an arbitrary network. Then,adversaries can learn whether edges exist between specific targeted pairs of nodes.

The work in [7] identifies an essential type of privacy attack,called neighborhood attacks. That is, if an adversary has some knowledge about the neighbors of a target node and the relationship among them, it is possible to reidentify the node from a social network. The authors modelled the k-neighborhood anonymization problem systematically and proposed an anonymization approach based on the neighborhood component coding technique, but admitted that the algorithm would be a computational serious challenge as the neighborhood size increased. It is believed that this observation is closely related to the subgraph knowledge queries discussed in [5].

Liu and Terzi [8] study a specific graph-anonymity model called k-degree anonymity that prevents the re-identification of individuals by adversaries with a priori knowledge of the degrees of certain nodes.

Definition 2.1. (k-degree anonymous [8]) A graph G(V, E) is k-degree anonymous if each vertex v ∈ V has the same degree with at least k ? 1 other vertices.

They provide a two-step framework for the k-degree anonymity problem: degree anonymization and graph reconstruction.The first step is solved by a linear-time dynamic programming algorithm, and the second step is solved by a set of graph construction algorithms that are related to the realizability of degree sequences. Experiments on a large spectrum of synthetic and real network datasets demonstrate that their algorithms are efficient and can effectively preserve the graph utility, while satisfying k-degree anonymity.

Zheleva and Getoor [19] consider the problem of protecting sensitive relationships among the individuals in the anonymized social networks. This is closely related to the link-prediction problem that has been widely studied in the link mining community.The work in [20] studies how anonymization algorithms based on randomly adding and removing edges change certain graph properties. More specifically, they focus on the change caused in the spectrum of the network.

Liu et al. [21] take weights as consideration for privacy preservation in social networks. They study situations, such as in a business transaction network, in which weights are attached to network edges that are considered confidential. Then, they provide two perturbation strategies for this application. In particular,their methods yield an approximate length of the shortest path, while maintaining the shortest path between selected pairs of nodes, but also maximize privacy preservation of the original weights. The research in [22] extends the above work by formulating an abstract model based on linear programming. However,the objective of their work focuses on maintaining a certain linear property of a social network by reassigning edge weights.

The work in [23] proposes a historically important algorithm in the field of community detection. The main idea behind is to first calculate the centrality for all edges and then invoke an iterative process that in each iteration removes the edge with the largest centrality and recomputes centralities on the running graph. A large variety of methods have been since developed based on the Girvan-Newman algorithm. Tyler et al. [24] presented a modified version of the algorithm that aims to improve the speed of the calculation. The work in [25] provides a modification of the Girvan-Newman algorithm in which vertices,rather than edges, are removed based on a vertex-based centrality metric. In addition, as the Girvan-Newman algorithm is unable to detect overlapping communities, both studies in [26]and [27] explore the modified algorithms in which vertices can be split between communities.

Another popular type of community detection methods is based on the so-called modularity [28] that is a stopping criterion for the Girvan-Newman algorithm. Since the problem of modularity optimization has been proved NP-complete [29],several heuristic algorithms are proposed to find approximations of the modularity maximum in a reasonable time, which are based on different techniques, including greedy technique[24], simulated annealing [30], extremal optimization [31], and spectral optimization [32]. An extensive study of community detection can be found in [9] for further reading.

In this section, we first provide some preliminaries and notation used throughout the paper. Then, a general model is proposed to define the weight anonymization problem (WA) for a graph. Furthermore, we consider an efficient metric to quantify the information loss incurred by the graph perturbation and its relations with other measures in previous studies. Finally, we discuss two concrete weight-related attacks.

An undirected and weighted graph G(V, E, W) is specified by its vertex set V , edge set E, and weight set W. The cardinalities are 'V' = n and 'E' = m, respectively. In most studies of graph theory, each entry in W is represented as a numeric label w(e) associate with each edge e ∈ E. Deviating from this convention,this paper considers a vertex-related definition as an alternative.

Definition 3.1. (weight bag) For each vertex v_i ∈ V, we define a weight bag for v_i as the sequence of weights on all edges connecting vi to other vertices, denoted by w_i = [w_i1, w_i2, …., w_idi](w_i1 ≥w_i2 ≥ … ≥ w_idi), where di represents the degree of v_i.

A weight bag can be a multiset, since different edges can have the same weight in real world cases. Then the weight set can be described as the complete set of weight bags in G, i.e., W= {w_i,…, w_n}, where n is the number of vertices. For example,the weight bag for the vertex b in Fig. 1a is w_b = [w_bc, w_ba] = [3,2] and the weight set for this three-point graph is W = {[2, 2],[3, 2], [3, 2]}. Although the following studies are restricted to undirected graphs, most of the results are suitable for directed cases by selecting edges with v_i as either a source or a sink in Definition 3.1.

In this paper, we allow weights to be integers, rational numbers or real numbers but non-negative. Given a graph G' (V, E',W') perturbed from G, the above constraint requires there are no negative entries in the perturbed weight set W'.

In general, a large variety of weight properties derived from the weight set can be used to identify a vertex. Let f be a function mapping W ？ P, i.e., P = f(w) w ∈ W. Note it is unnecessary for f to be a linear function. Here, we say P is the weight property corresponding to the function f. Assume that P_i ∈ P is the weight property for vertex v_i. Then, if P_i has the unique value in P and has been known by an adversary, v_i can be successfully identified from the graph. Hence, we first introduce the following term about the k-weight anonymous graph.

Definition 3.2. (k-weight anonymity) A graph G is k-weight anonymous if for every vertex v, there exist at least k ? 1 other vertices in the graph with the same weight property P ∈ P as v.

Let C_A be the cost during weight anonymization and C denote the information loss incurred in the entire perturbation process.For a weight property P, we formally propose the weighted graph anonymization (WGA) problem as follows.

Problem 3.3. (weighted graph anonymization) Given a graph G(V, E, W) and an integer k, find a k-weight anonymous graph G'(V, E', W') according to the weight property P, such that both C_A and C = (C; C_A) are minimized.

The information loss is a critical measure to quantify the utility of a perturbed graph, and we will introduce efficient metrics in the next section. Most previous work [9, 21, 22] uses a twostep strategy that splits the problem into two sub-problems,called property anonymization and graph reconstruction, to solve graph perturbation problems. The idea behind this is to reform the structure of a graph according to either its randomized weight matrix or anonymized property sequence. For each step, the methods are devoted to minimizing the information loss incurred by perturbation or reconstruction. Such a strategy is quite attractive for large graph anonymity due to its reasonable complexity in real applications. Therefore, all methods proposed in this paper will follow this track.

From a general view, each privacy preserving approach has its limitations due to the wide concepts of data privacy and utility,which means it only works efficiently on protecting data from a certain family of attacks and maintaining pre-specified data utility. There is no exception here. The task to determine an efficient measure becomes even more complex in graph analysis due to its topological structure.

Differentiating from some other problems, such as k-anonymity on transactional data, we use a conditional metric C =(C; C_A) to assess the quality of an approach for the WGA problem.The anonymizing cost C_A is usually related to the operations of anonymization, while C represents one of the real graph properties that we suppose to preserve. Here, we can only guarantee a solution of C to be optimal for WGA with the condition of certain C_A. It can be seen as a trade-off between utility and efficiency. That is, an anonymizing algorithm becomes too complex to implement with a real graph property as C_A, since it must construct the adjacency matrix to obtain the real property at each perturbation step. Intuitively, we expect there exists a tight and determined relation between C_A and C, leading to an optimal solution in the whole process. However, the difficulty to find such a relation relies on the selected metrics. The metrics for both of them can vary within different applications.

1) Anonymizing Cost:The privacy metric for anonymity is indistinguishing level k in general. Besides the security requirements,we also expect the perturbation to have a minor effect on the original data. As our basic operations for perturbation is to add, delete or reallocate edges/weights in graphs, the method for weight anonymization is naturally required to minimize the changes of weights. Some previous work in [8] quantifies anonymizing cost, using the number of edges changed before and after graph perturbation. We first consider extending this metric as anonymizing cost in the WGA problem. Given a sequence of certain weight property w = [w1 . . . , wn], the anonymizing cost incurred by property anonymization is mathematically formalized as follows,

where m is the number of anonymizing groups, gi and wi* represent the number of objects and the anonymizing object in each group. Although it is quite simple and intuitive to use CA as the anonymizing cost incurred in the perturbation, the underlying relationship between such anonymization cost and the topological structure of a graph is still unclear. However, our extensive experimental results with real-world data have shown its efficiency,which implies underlying relations with real graph properties.

2) Spectrum-based Information Loss: Our next task is to define an efficient metric for information loss. In this paper, we consider a spectrum-based metric derived from the spectral graph theory. Recall that, the Laplacian matrix of a weighted graph G(V, E) is defined as L = D ? A, where D and A are the degree matrix and the adjacency matrix respectively. The set of eigenvalues of L, λ = (λ1, λ2, . . . , λn), is called the spectrum of G. If the graph only contains one component, we have 0 = λ1 ≤λ2 ≤ . . . ≤ λn. Many studies [33-35] point out that the spectrum plays a central role in understanding of graphs, since it is closely related to most invariants of a graph, such as mean distance,diameter, connectivity, expanding properties, maximum cut, isoperimetric number and randomness of the graph. Particularly,the second smallest eigenvalue λ2, known as algebraic connectivity, has been discovered in its application to several difficult problems in graph theory. In this paper, we use the bias of λ2 to measure the information loss. Let λ2 be the second smallest eigenvalue of the anonymized graph G'. Then, the information loss C is defined as

Therefore, an anonymizing algorithm aims to find a perturbation to minimize Equation 2, while guaranteeing the privacy of entities in the graph.

Now, we discuss the relation between C_A in Equation 1 andλ₂. The following theorem describes impacts of the weight modification on the spectrum.

THEOREM 3.4. λ₂ ≤ λ₂ whenever G' is obtained from G by increasing the weight value on an edge. Similarly, λ₂ ≥ λ₂ whenever G' is obtained from G by decreasing the weight value on an edge.

The proof of THEOREM 3.4 is omitted here due to the space limitation. THEOREM 3.4 shows the change of weights can approximately estimate the bias of λ₂, this leads to an efficient way to develop anonymization algorithms. It is ideal to quantify the relation between λ₂ and the modification of weights with a determined function λ₂ = f(W). However, exploring such a function is still an open problem in the matrix perturbation theory. In this paper, we allow single operation only, i.e., either increasing weight or decreasing weight. With such an assumption, the optimal anonymization problem can be reduced to the problem of minimizing the weight changes C_A in the anonymization progress.

Equation 1 only provides an efficient measure to achieve the minimal information loss in designing an anonymization algorithm.However, the bias of the spectrum can be influenced by reconstructing a graph as well. The work in [36] provides theoretical analysis of reconstructing a weighted graph from its spectrum, which maintains the eigenvalues perfectly. However,the conditions for reconstructability of weighted graphs are only sufficient and it can be costly to implement. Therefore, we provide efficient methods for graph construction with the objective of minimizing the information loss C in a later section.

There exist a variety of weight properties in a weighted graph. Based on the general model for weight anonymity, we will discuss two types of weight-related attacks and apply the general model on these anonymization problems.

1) Volume Attack: We first consider a weight property, called volume, which describes the sum of a weight bag. That is, the function f = Σ, and for a vertex vi, Pi =Σj=1di wij. Notice that, the value of the volume is sometimes used as degree in research on weighted graphs, but we use it separately for a clearer statement.Using si to specifically represent the volume of vi, we can form a sequence S = [s1, . . . , sn] (s1 ≥ s2 ≥ . . . ≥ sn), where n is the number of vertices. It is easy to find that, if there exists a unique si in S and the value is known by an adversary, the entity represented by vi will be identified from the published graph.We term this privacy breaching process a volume attack. Correspondingly,we can define k-volume anonymity for a graph as follows.

Definition 3.5. (k-volume anonymity) A graph G is k-volume anonymous if for every vertex v ∈ V, there exist at least k ? 1 other vertices in the graph with the same volume as v.

For example, the graph (a) in Fig. 1 is 1-volume anonymous,since S = [5, 5, 4]. The graph (b) is 2-volume anonymous, as S =[6, 6, 5, 5].

2) Histogram Attack: Another weight-related attack refers to the histogram of a weight bag. In statistics, a histogram is a graphical display of tabular frequencies. Let Bi be the set of histogram bins for the vertex vi and each bin consists of weights falling in the bin range. We use Bi = (bi1, bi2, . . . , bim) to represent the set of bin frequencies for vi, where bij is the number of elements in the corresponding bin and m is the number of bins.Here, we assume the partitioning of histogram bins is the same for all vertices. Then, we can define k-histogram anonymous for a graph, as follows.

Definition 3.6. (k-histogram anonymity) A graph G is k-histogram anonymous if for every node v, there exist at least k?1 other node in the graph with the same histogram as v.

A special case of histogram attack is that weights are all integers and the bin width in every histogram is 1. Then, the similarity of histograms can be transferred to the similarity of weight bags. We say two weight bags are equal if and only if they have the same elements and the same multiplicity for each element. The graph (a) in Fig. 1 is 1-histogram anonymous as W= {[3, 2], [3, 2], [2, 2]} and (b) is 2-histogram anonymous as W= {[3, 3], [3, 3], [3, 2], [3, 2]}.

3) Discussion: It is worth discussing the relationships among various weight anonymity problems, since this may provide alternatives to design anonymization algorithms. The degree anonymity is also considered as a special case of weight anonymity.We have the following proposition.

PROPOSITION 3.7. If a graph G is k-histogram anonymous,then it is also k₁- degree anonymous and k₂-volume anonymous,where k₁, k₂ ≥ k.

The proof is obvious with the equality property of weight bags. This proposition shows that an approach for histogram anonymity achieves degree and volume anonymity at the same or a higher security level. We have to point out that Proposition 3.7 is just a sufficient condition. That is, degree and volume anonymity cannot guarantee the same level of histogram anonymity.

In this section, we consider methods to protect a graph from histogram attack. Based on our general model and the definition of k-histogram anonymity, the histogram anonymization (HA)problem is formally defined as follows.

Problem 4.1. (histogram anonymization) Given a weighted graph G(V, E, W), and an integer k, construct a k-histogram anonymous graph G'(V, E', W') such that the information loss C is minimized.

The solution to Problem 4.1 follows the two-step strategy discussed in the previous section. It first tries to find the optimal anonymity W' for W with the minimal cost C_A, and then constructs a weighted graph with W' and the original vertex set V.Now, we introduce algorithms for these steps respectively in the following two parts.

The first challenge in histogram anonymization is to perform appropriate data preparation for the calculation of information loss, since weight bags in a weight set may come in different sizes. Considering each weight bag as a point in a unified multidimensional space, the preparation procedure is required to maintain these points as densely as possible. Mathematically,for a vertex v_i, its weight bag w_i = [w_i1, . . . . , w_idi] can be seen as a vector in the d_i-dimension space, where di is the degree of vt. If let m = max(d_i) i ∈ [1, n], we can map all weight bags in W to the m-dimension space, denoted as U_m×n, in which each weight bag is represented by a column vector with length m. This mapping procedure will expand weight bags with d_i < m by filling(m ? d_i) zeros.

LEMMA 4.2. Given a graph with a weight set W, the k-weight anonymization with the lowest cost C_A can be achieved if every column vector in the set U is sorted in descending order.

Proof: Recall that a weight bag is defined as a sorted multiset.Let W_p be a weight bag with 'W_p' = m and W_q be a weight bag with 'W_q' = m ? 1. Assume that U_q and U_q^' represent the mapped vectors with and without in descending order respectively.

Let us say U_q = [w_q1, . . . . , w_q(m?1), 0] and U_q^' = [w_q1, . . . , 0,w_q(m?1)]. It is simple to see that ∥U_p - U_q∥.< ∥U_p> -U_q^'∥. All other cases of U_q^' can be justified by iterative process.

Lemma 4.2 is a necessary condition for an anonymization algorithm to achieve the lowest cost. It implies that, to guarantee the lowest information loss, we have to assign 0s to the end of weight bags whose sizes are smaller than m. For instance, in

[101] Algorithm 1. Histogram anonymization algorithm

Algorithm 1. Histogram anonymization algorithm

Fig. 1b, if we connect the vertices a and d with weight 1, we have the weight set as W = {[3, 2, 1], [3, 2], [3, 3], [3, 3, 1]}.Then, this set can be mapped to a 3-dimension space as U = [3,2, 1; 3, 2, 0; 3, 3, 0; 3, 3, 1]^T.

Another issue in the HA problem is to determine the anonymous object for data generalization in each anonymous group.Generally, these objects are expected to be chosen from the original dataset. However, this constraint is too strict for histogram anonymization, as the unique weight operation is allowed only so far. Here, we relax the constraint to allow the method building the ‘largest’ vector as the anonymous object. That is,for a group g_i = (u₁, . . . . , u_q), we generate a vector as its anonymous object, where u_i,j^*= max_j(u_ij). For example, given U= [3, 2, 1; 3, 2, 1; 2, 2, 1; 3, 3, 0]^T, a vector u* = [3, 3, 1]^T is formed as the anonymous object for U.

The complexity of this problem has not been assessed, as far as we know. However, the work in [37] discusses a similar problem with the u* being the mean vector of a group that has been proven NP-hard. Although it is unclear whether the HA problem can be inducted from this existing problem, we can prove its NP-hardness using a similar induction process, omitted here due to space limitation. Therefore, we describe an efficient heuristic algorithm as a solution in Algorithm 1.

The computational complexity of Algorithm 1 is O(n²log□).Here, we form a symmetric n × n distance matrix in which each entry represents the Euclidean distance between two weight bags in U. This reduces the complexity of the initialization step to linear. The algorithm introduces O(n²) operations to calculate all new distances among groups in each recursive step. Finally,there are log□ recursions due to the group merging. Therefore,the total complexity is

Graph construction is the second stage of the two-step strategy that aims to construct a graph with an anonymized weight set. The graph construction based on a specified degree or volume sequence has been extensively studied in previous work[38-40]. Although the k-histogram anonymity guarantees the kvolume anonymity, the realizability of volume sequences is insufficient for that of weight sets. Therefore, by a given weight set W, we provide a Weighted Graph Construction (WGC) method based on edge removal in Algorithm 2.

The WGC algorithm takes the specified weight set W as inputs and returns either a successfully constructed graph or“Fail”, meaning W is not realizable. Step 2 is a basic condition to ensure the total degree of the graph is even. For a vertex,Steps from 6 to 9 describe an efficient procedure to remove edges by matching each element in its weight bag. Specifically,for a picked vertex v_r, when it chooses a candidate v_s to join, the procedure has to ensure w_s contains an element w_sj that appears in w_r as well, i.e., _wsj = _wri. The lay-off procedure for sequence realizability only guarantees the sum of weights and the combination of edge connections can vary. The constraint introduced by histogram anonymity can be too strict to satisfy. This may break the weight anonymity but significantly increase the success rate of constructing a graph. In addition, it is still impossible for an adversary to identify an entity, since the weight will be increased anyway. In practice, we can relax the condition w_sj= w_ri as 'w_sj ? w_ri' < β, where β? is a specified threshold. As we show in our experimental evaluation, the constructing algorithms can successfully generate anonymized graphs in most cases with a small value of β. Step 11 is to ensure the connectivity of the output graph. That is, if the construction results in a graph with several components, it will bridge them by swapping certain edges. For example, assuming that (v_i, v_j) ∈ E_G^1' and (v_r, v)∈ E_G2^' with w_ij = w_rs, where G' = G₁' ？ G₂' and G₁' G₂' = Φ, the graph G' can achieve complete connectivity by swapping (v_i, v_j)and (v_r, v_s) as (v_i, v_r) and (v_j, v_s). If the algorithm terminates and outputs a graph, then this graph has the specified weight set W.

The computational complexity of Algorithm 2 is O(n₂m₂),where n is the number of vertices and m is the maximal degree for all vertices. For each vertex v_i, there are maximal m edges connecting vi with other nodes. For each edge, the worst case is traversing all remaining vertices to find v_s, which is n × m times. As there are n vertices, the total complexity is O(n₂m₂).

Notice that, Step 7 makes a trade-off between efficiency and accuracy in Algorithm 2, as there may exist a group of vs and this may result in various information losses by connecting vr to different vs. We provide a sort-then-switch procedure on the edge set of a constructed graph to optimize the information loss incurred in graph construction (the implementation of this procedure is omitted here). The procedure takes a constructed graph G and the eigenvalue λ₂ computed from the original graph. The idea is to determine the range of switching candidates by sorting the edge set first, and then switch edges to find the connections leading to the closest eigenvalue to λ₂. The complexity of this procedure is O(n³m²). in the worst case,where n and m are the sizes of V and E, respectively, while the major cost is to calculate the eigenvalue in each iteration with the standard eigen decomposition taking O(n³) operations. However,it can be significantly improved using eigenspace approximation techniques, such as the Lanczos algorithm and its variation [41]. Moreover, let p be the size of the switching set with maximal candidates. Our experiments show that the value p is much less than m in general; this means the inner iteration in Step 5 only has a small number for real graphs. Therefore,Algorithm 2 is also efficient to work on large scale graph data

[102] Algorithm 2 Weighted graph construction algorithm

Algorithm 2 Weighted graph construction algorithm

with the sort-then-switch procedure.

In this section, we evaluate the performance of the proposed graph anonymization algorithms. The experiments are conducted on a 2.16 GHz Intel Core 2 Duo Mac with 4 GB of 667 MHz DDR2 SDRAM running the Macintosh OS X 10.5.8 operating system. All algorithms are implemented using Matlab 7.0.

We use both synthetic and real-world datasets. For experiments with synthetic data, we generate a random weighted graph G_r with n nodes randomly connected to each other with a specified probability p. Here, we set n = 2; 000 and p = 0.5. For each edge, the model assigns a random integer weight in the range [1, 100].

We also use two real-world graph datasets, named BkFrat and NetSci, respectively. All these graphs are weighted and undirected. The BkFrat graph [42] concerns interactions among students living in a fraternity at a West Virginia college. The graph contains 58 nodes with all integer weights in the range of[0, 51]. The NetSci graph [10] contains a coauthorship network of scientists working on network theory and experiments.

The version given here consists of 1; 589 scientists and assigns real weights as described in [43]. All the testing data have been simply generalized by removing all real labels for their vertices. All the real-world graph datasets are available at http://www-personal.umich.edu/~mejn/netdata/.

Our first experiment is to show how possible weight attacks may occur on realworld graphs. We consider both volume attack and histogram attack, and provide results of degree attack as a comparison. Table 1 shows our results. The parameter α is a threshold to assess a breach. That is, while the number of vertices sharing the same value of a weight property is no larger than α, these vertices are considered to be disclosed. It clearly shows that weight attacks are a real issue for graph data publishing.All testing datasets have relatively high risk of entity disclosure.For BkFrat data, the success rate of volume attack withα = 1 is as high as 93%, and even as high as 98% for histogram attack, implying that most of its vertices can be uniquely identified.In addition, the disclosure risk grows quite fast as αincreases. For example, the success rate of volume attack on the NetSci dataset increases nearly 10&#37; with α = 10 than that with α = 1.

[Table 1.] Weight attacks on real-world data

Weight attacks on real-world data

Moreover, the results show that weight attacks have much higher success rate to breach a dataset than degree attack. This means such attacks are more practical in real-world scenarios.In addition, both weight attacks maintain similar success rates,while the impact of degree attack is decreased significantly, as the data size increased. The result for NetSci data shows there are 11:01% vertices with high disclosure risk, as α = 10 for volume attack. That is, around 180 entities have the possibility of being identified. However, the number is only 46 for a degree attack.

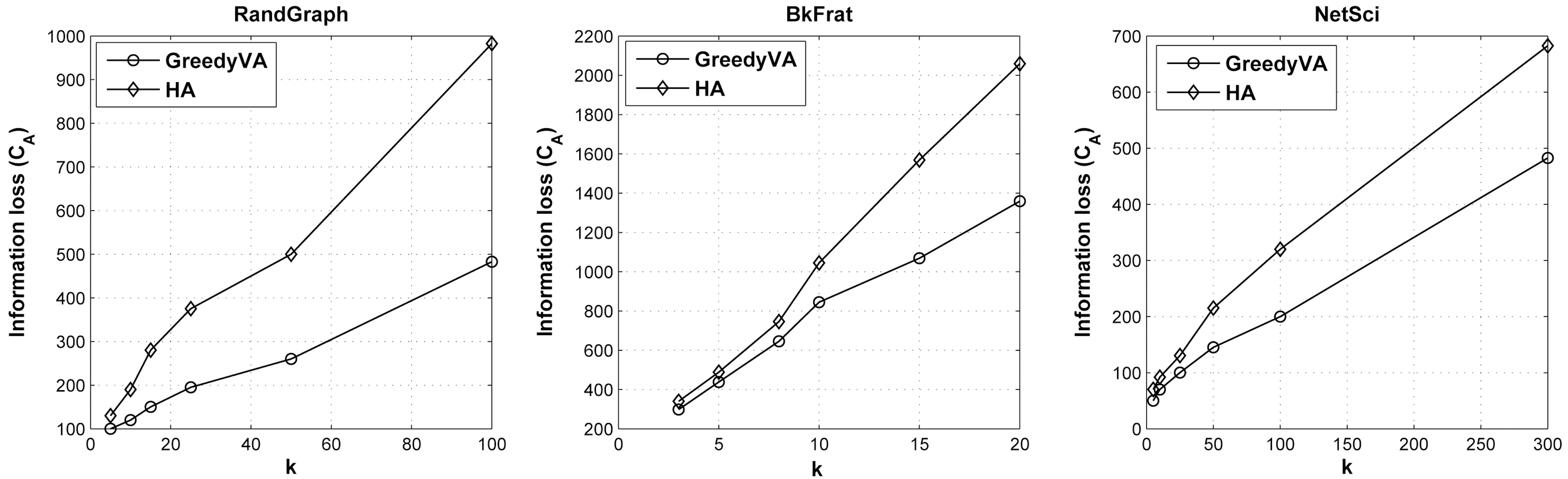
In this section, we assess the qualitative performance of information loss incurred by applying histogram anonymization.As a comparison, we also implement a greedy anonymization algorithm for volume attack, termed GreedyVA, modified from degree anonymization [8] by replacing the degree sequence with volume sequence.

The graphs in Fig. 2 describe the relations between anonymization cost C_A and various k for the RandGraph, BkFrat, and NetSci datasets, respectively. The results show that the anonymization costs increase slowly, while k is not large (e.g., k < 20 in RandGraph or k < 50 in NetSci) for both anonymization algorithms.In addition, we note that the HA results in a bigger cost,as expected, than the GreedyVA, in all cases. However, the relative differences are much smaller in real-world data than in the synthetic graph.

[Fig. 2.] The relation between CA and k.

[Fig. 3.] The relation between C and k.

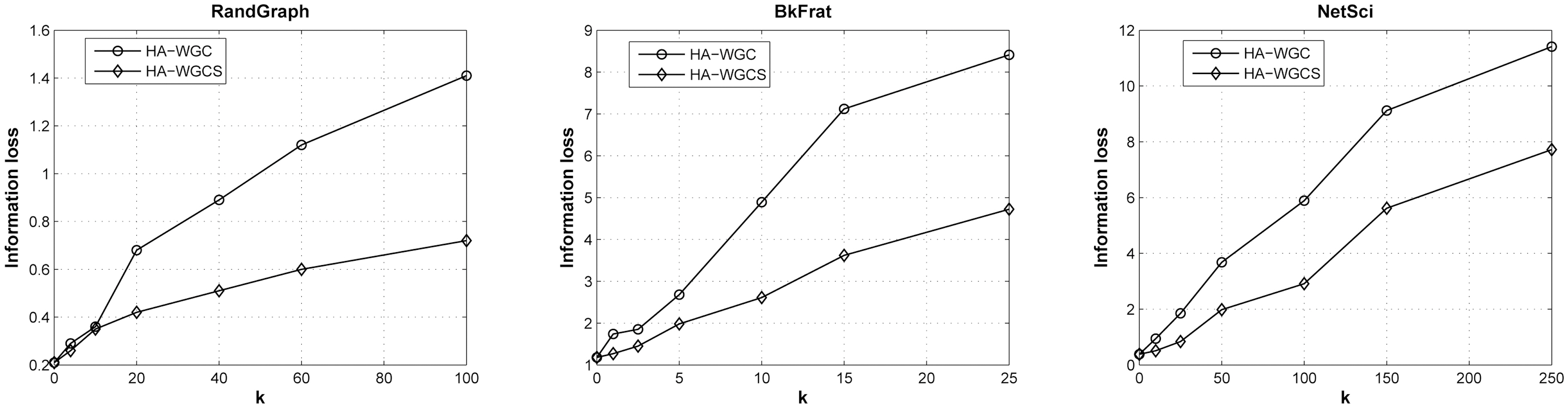
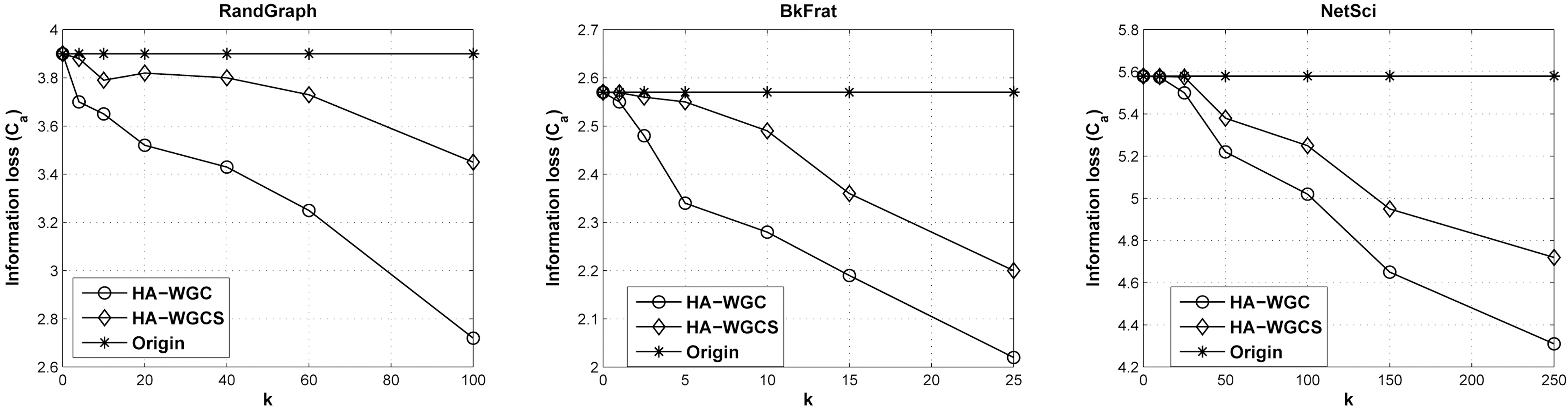
1) Impacts on Graph Spectrum: We evaluate and compare the information loss for the complete histogram anonymization.Fig. 3 summarizes the impacts on the spectrum λ2 on the Y-axis,varying k for the testing datasets. Two construction methods are compared here: WGC (HA-WGC) and WGC with the sort-thenswitch procedure (HA-WGCS). From the plots, we can observe the sort-then-switch procedure can significantly improve the utility performance of histogram anonymization. For example,in RandGraph, such a procedure reduces the bias of information loss from 1.4 to 0.6 for k = 250. The gap is insignificant for NetSci compared to other data, and it is not obvious to decide on the major reason.

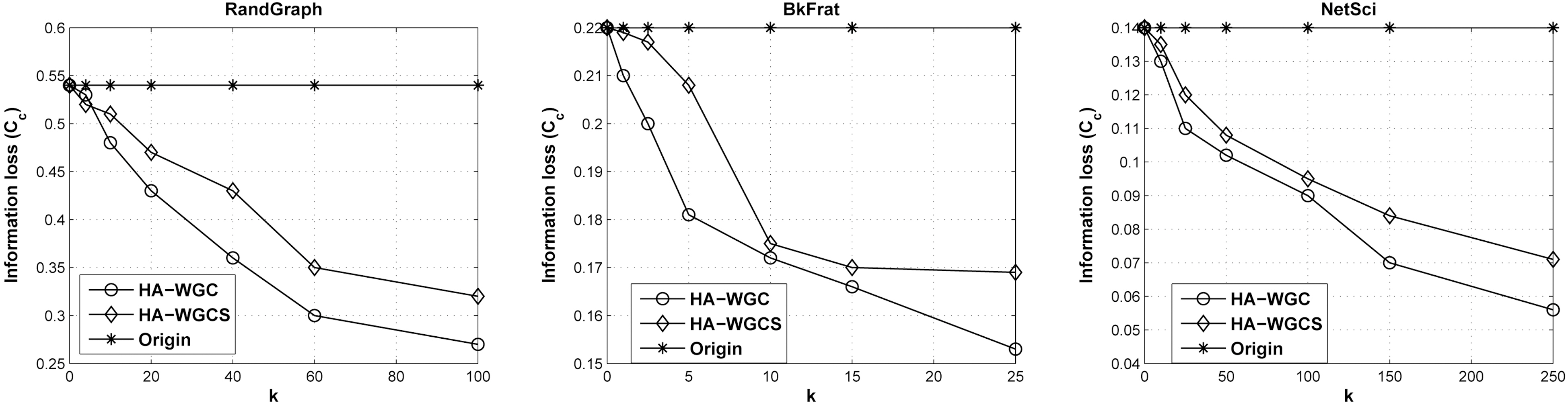
2) Impacts on Real Graph Characteristics. As mentioned above, the spectrum of a graph has close relations with many real graph characteristics. In this section, we evaluate the information loss based on real graph characteristics of the test data with the algorithms of HA-WGC and HA-WGCS. We focus on two of the most robust metrics of network topology. The first is the global clustering coefficient that is a measure of the degree to which nodes in a graph tend to cluster together. A generalized clustering coefficient is formally defined in [44] as

where ω_Δ is the total value of triangles and ω₃ is the total value

[Fig. 4.] The relation between CC and k.

[Fig. 5.] The relation between Ca and k.

of triplets. In addition, we define the value of a triplet as the geometric mean of the weights of ties. The second one is the weighted average path length, C_a, this is defined as the average cost of steps along the shortest paths for all possible pairs of network nodes.

Figs. 4 and 5 show the relative changes of the real graph properties C_c and C_a with HA-WGC and HA-WGCS approaches by varying _k. In each figure, a constant line appears to the property value of the original graph, which is unaffected by the value of _k. As expected, the anonymization process decreases both graph properties, since new edges and weights are increased. The results show that HAWGCS maintains both real graph properties much better than does HA-WGC; this corresponds to the impact on the spectrum. In addition, it is easy to observe that HAWGCS can lead to very small bias of property values from their original values in both cases.

So far, we have extensively explored the problem of privacy preservation on weighted graphs against weight-related attacks.The theoretical and experimental results show that our algorithms perform effectively on not only protecting graphs from identity disclosure, but also maintaining elementary graph properties,such as spectrum, clustering coefficient, and average path length. Such utility preservation can guarantee the data quality for statistical analysis applications. However, it is poor in answering the following question: how the proposed methods will affect data quality for data mining analysis.

In this section, we discuss how to extend our approaches to ensure the quality of graph clustering with published data. This is known as community detection in the related field. Instead of providing a comprehensive solution for privacy preserving graph mining, our intention is just to show that the proposed methods can be used to solve concrete data mining problems with only slight modification.

According to the basic preliminaries in Section III-A, we can introduce notation for community description. A natural approach for graph clustering is based on the concept of graph cut. In graph theory, a cut of a graph G(V, E, W) is a proper partition of the vertices of a graph into two disjoint subsets. The cut-set of the cut is the subset of edges S ⊂ E whose end points are in different subsets of the partition. Edges are said to be crossing the cut if they are in its cut-set. The weight of a cut is the sum of the weights of all edges in S. A minimum cut of G is a cut of minimum weight. The weight of a minimum cut is called edge connectivity of G and denoted by s_G. A cut and its complement can naturally be identified with each other.

Then, we can initially introduce a popular definition of community based on edge connectivity, as follows:

Definition 6.1. (community [12]) Let G(V, E, W) be a graph and H ⊆ G a subgraph. A community generated by H is a subgraph C of G, such that

(1) H ⊆ C,

(2) sC ≥ sH' for each subgraph H' ⊆ G with H ⊆ H',

(3) H' ⊆ C for each subgraph H' ⊆ G with H ⊆ H'and sC = sH'.

The above definition interprets a community as the largest subgraph of maximal edge connectivity among all subgraphs of G containing H. The family of all communities of G is denoted by O_G. Then, our objective is to minimize the change of O_G.That is, an anonymized graph G' is required to maintain the similar communities as the original graph.

Appropriate metrics need to be defined in advance to quantify the information loss of graph anonymization on community detection. We first consider an intuitive metric, termed intragroup error, which records the local information loss. Let a matrix A_n×n present the pair-wise relations of vertices according to a community set O, where a_ij = 1 if vertices v_i and v_j belong to the same community and a_ij = 0 otherwise. Then, assuming O_G and O_G' are generated by G and G' respectively, the intra-group error is defined as,

where a_ij is the corresponding entry of a_ij in A'. This metric describes the direct difference in each community with a very easily understood concept.

Another important metric for community detection is modularity,known as a global quality function to identify good partitions[9]. One of the most popular concepts of modularity is proposed by Newman [45]. It is based on the idea that a random graph is not expected to have a cluster structure, so the possible existence of clusters is revealed by the comparison between the density of edges in a subgraph and the density one would expect to have in the subgraph, if the vertices of the graph were attached, regardless of community structure. This expected edge density depends on the chosen null model, i.e. a copy of the original graph keeping some of its structural properties but without community structure. Mathematically, the modularity M of a partition of a graph into clusters is

where N_G is the number of communities, L is the number of edges in the graph, l_C is the number of edges between vertices in community C, and d_C is the sum of the degrees of the nodes in C. It is clear that l_Lis the ratio of edges inside community C, and

pproximates the ratio of edges that one would expect to have inside the community from chance alone. Let M_G and M_G' be the modularity derived from G and G' respectively.Then, we can define the modularity bias as information loss:

In this part, we provide a community preservation procedure aiming to minimize the change of the community set O_G. Our main idea is to first assign a two-way label for each vertex v ∈ V in G(V, E, W) according to the community and the min-cut that contains it. Then, we perform vertex addition or deletion only in its incident domain(s). For example, assuming that a graph G has two non-overlapping communities C₁ and C₂ with the mincut S, a label (C₁, S_v) for a vertex v ∈ V implies v ∈ C₁ and v ∈S_v. We also use S₀ as a virtual set to denote a vertex does not appear in any min-cuts. Therefore, in both graph construction algorithms, we can perform the selection of v_s within the domain in which the elements have the same label. Apparently,this procedure is application-oriented, since a number of algorithms exist for community detection. However, this limitation can be released in the real-world applications, in which the data publisher can make consistent standards on the methods of community detection with data users.

In this section, we evaluate the impact of graph anonymization on community detection in terms of the proposed metrics.The experimental setup and testing data are the same as that in Section V.

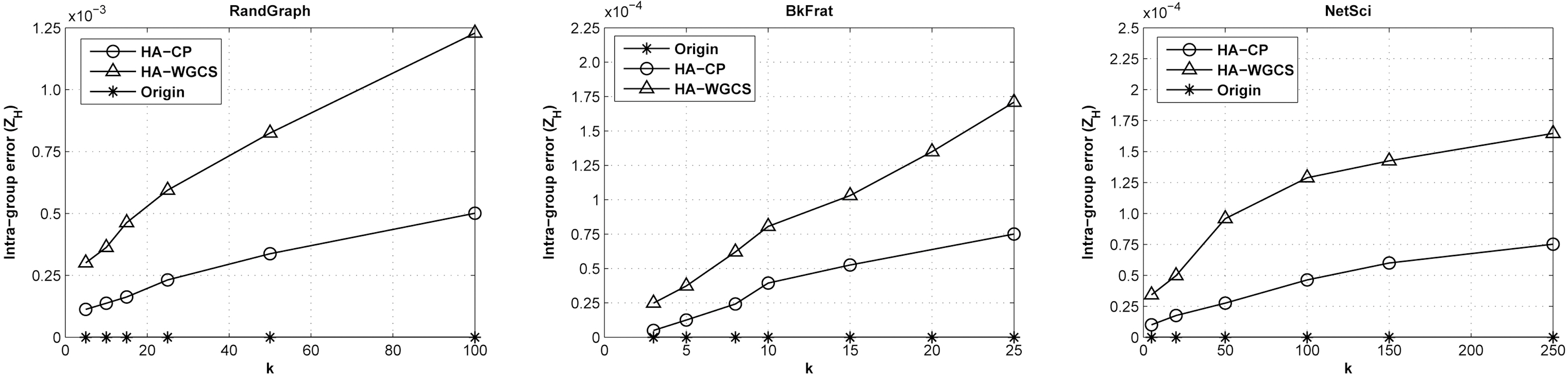
1) Intra-group Error ZH: We first assess the intra-group error defined in Equation 3 for graph anonymization. We compare two approaches: the basic HA-WGCS algorithm and the HA-WGCS algorithm with the community preserving procedure(HA-CP).

Fig. 6 summarizes the intra-group error Z_H on the Y-axis with varying k for the testing datasets. It is obvious that Z_H is monotonically increasing with k for all testing cases. Therein,the HA-CP approach outshines the comparison in all plots. The results show HA-CP can maintain significantly better graph clustering than the method that does not consider community

[Fig. 6.] The relation between ZH and k.

[Fig. 7.] The relation between ZM and k.

preservation during the perturbation process. In addition, it reveals that this method can still maintain a relatively low information loss, even for a large k. That is, the proposed approach can better preserve the utility without sacrificing much privacy protection.

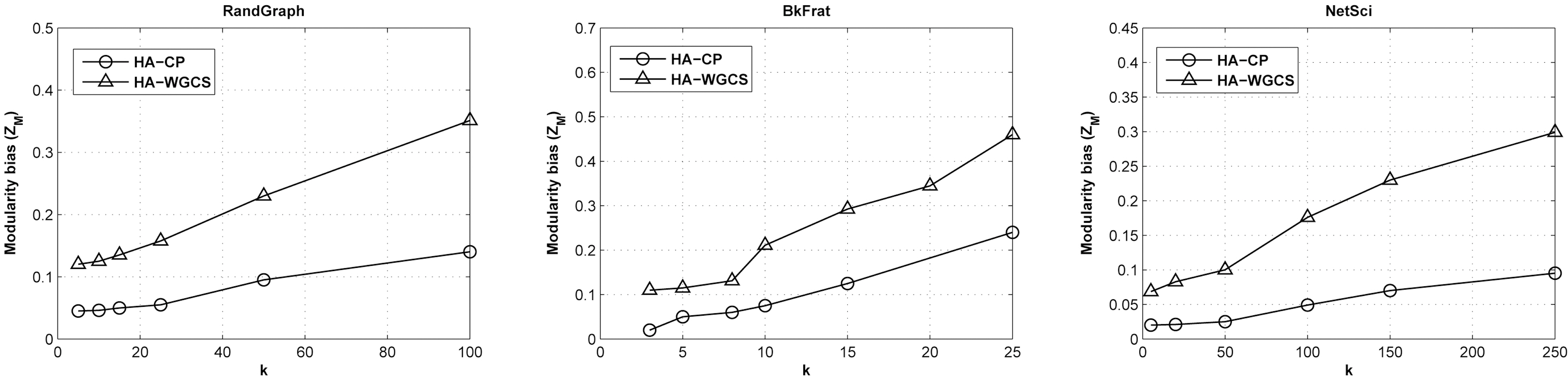
2) Modularity Bias ZM:The second experiment explore the relationship between the modularity bias defined in Equation 4 and k. Fig. 7 shows the relative changes of ZM with HA-CP and HA-WGCS by varying k. The modularity bias increases as k increases that follows the similar trend of ZH. However, the gradients are not as steep as that of ZH, especially when k is not large. This implies that the impact of perturbation on modularity is insignificant as the intra-group error, as ZM is a global measurement.In addition, HA-CP performs much better than HAWGCS in all cases, as expected. Moreover, the BkFrat data have the smallest difference, especially when k is not large (< 10).The reason for this is still unclear and we suppose it is related to certain structural properties of the dataset itself.

It is clear that the community preservation scheme can significantly improve the quality of community detection. However,in all experiments, we can see that HA-WGCS also has reasonable performance on community preservation, when the privacy level is not too high. This implies that in the real-world scenarios, HAWGCS is also practicable.

In this paper, we discussed a class of important background knowledge attacks in a weighted graph. We provided a general model for the weight anonymization problem to defend against weight-related attacks. As a proof of concept, we considered the k-volume anonymity and the k-histogram anonymity as two cases that could occur in the real-world privacy graph data publication.We provide a complete solution to achieve both volume anonymity and histogram anonymity using the graph spectrum as an effective metric for information loss. We also analyzed the complexity of the models, and experimentally validate our analysis using both synthetic and real-world weighted graphs. Finally, we extend our work to preserve the quality of community detection that is a popular application in the graph mining field.

Many issues of this work need that to be addressed clearly merit further research. As a NP-hard problem, it is worth developing approximation algorithms for the histogram anonymization problem. Also, if we allow random weight modification(increment and decrement), the impact on graph spectrum has to be reconsidered. In addition, this paper only evaluated the clustering coefficient and average path length as real-graph properties,and the affect on other topological structures is still unclear.