With the availability of an ever increasing number of transistors, higher power density and longer wire delay, microprocessor designers have chosen to integrate multiple cores onto a single chip rather than adding complexity to a single-core CPU. While multi-core processors for the desktop and server markets have gained much attention, the embedded industry is also increasingly adopting the multi-core design. The examples of embedded multi-core processors include the dual-core Freescale MPC8641D, dualcore Broadcom BCM1255, dual-core PMC-Sierra RM9000x2, quad-core ARM11 MPcore and quad-core Broadcom BCM1455 etc. Compared to uniprocessors, multi-core chips can offer many important advantages such as superior performance, higher power efficiency, lower temperature and better system density, all of which are important for embedded systems as well. In particular, with the growing demand of high performance by high-end real-time applications such as HDTV and video encoding/decoding standards, it is expected that multi-core processors will be increasingly used in real-time systems to achieve higher performance/throughput cost-effectively. Actually, it has been recently projected that real-time applications will be likely deployed on large-scale multi-core platforms with tens or even hundreds of cores per chip fairly soon [Calandrino and Baumberger 2007].
For real-time systems, especially hard real-time systems, it is crucial to obtain the worst-case execution time (WCET) of each real-time task, which will provide the basis for schedulability analysis. Missing deadlines in those systems may lead to serious consequences. While the WCET of a single task can be measured for a given input, it is generally infeasible to exhaust all the possible program paths through measurement. Another approach to obtaining WCET is to use static WCET analysis (or simply called WCET analysis). The WCET analysis typically consists of three phases: program flow analysis, low-level analysis and WCET calculation. While the program flow analysis analyzes the control flow of the assembly programs that are machine-independent, the low-level analysis analyzes the timing behavior of the microarchitectural components. Based on the information obtained from the program flow analysis and low-level analysis, the WCET calculation phase computes the estimated worst-case execution cycles by using methods such as the path-based approach [Healy et al. 1995; Stappert et al. 2001] or IPET (Implicit Path Enumeration Technique) [Li and Malik 1995; Li et al. 1996].
There have been many studies on WCET analysis, and most efforts have focused on analyzing the WCET for single-core processors [Healy et al. 1995; Stappert et al. 2001; Li and Malik 1995; Li et al. 1996; Ottosson and Sjodin 1997; Puschner and Burns 2000; Hardy 2008; White et al. 1997; Ramaprasad and Mueller 2005; Lundqvist and Stenstrom 1999a; Staschulat and Ernst 2006]. A good survey of WCET analysis can be found in [Wilhelm et al. 2008]. Recently, Rosen et al. [2007] studied the WCET analysis and bus scheduling for real-time applications on multiprocessor system-onchip(MPSoC). Although this approach considered the implicit bus traffic due to cache misses by different processors, it did not investigate the challenging problem of interthread cache interferences in a shared cache, which is common in multi-core processors. Also, Rosen et al.’s work is limited to a specific MPSoC architecture without shared caches, whereas this paper aims at developing a WCET analysis for a generic multicore chip with shared caches. Stohr et al. [2005] examined the WCET estimation in a symmetric multiprocessor (SMT) system. However, the latter approach is based on measurement alone, which is generally unsafe as it is impossible to exhaust all possible paths with various inputs.
The WCET analysis for multi-core processors is a very challenging task. Even for today’s single-core processors, many architectural features such as cache memories, pipelines, out-of-order execution, speculation and branch prediction have made the “accurate timing analysis very hard to obtain” [Berg et al. 2004]. Multi-core computing platforms can further aggravate the complexity of WCET analysis due to the possible inter-thread interferences in shared resources such as L2 caches, which are very difficult to analyze statically. While there have been recent studies on real-time scheduling for multi-core platforms [Calandrino and Baumberger 2007; Calandrino and Anderson 2007; Anderson et al. 2006], all these studies basically assume that the worst-case performance of real-time threads is known. Therefore, it is a necessity to reasonably bound the WCET of real-time threads running on multi-core processors before the multi-core platforms can be safely employed by real-time systems.
As the first step towards WCET analysis of multi-core processors to enable reliable real-time computing, this paper examines the timing analysis of shared L2 instruction caches for multi-core processors1. In this paper, we assume that data caches are perfect, thus data references from different threads will not interfere with each other in the shared L2 cache2. We propose to exploit the program control flow information (i.e., loops) of each thread to safely and efficiently estimate the worst-case L2 instruction cache conflicts. Built upon the static cache analysis results, we integrate we integrate them (ED note: by them do you mean results? Please, specify) with the pipeline analysis and path analysis to calculate the WCET for multi-core processors.
The rest of the paper is organized as follows. First, we discuss the difficulty of WCET analysis for multi-core chips with shared caches due to the timing anomalies in Section 2. In Section 3, we describe our approach to computing the worst-case shared L2 instruction cache performance and the WCET for multi-core processors. The evaluation methodology is given in Section 4, and the experimental results are presented in Section 5. Finally, we conclude this paper in Section 6.
2. DIFFICULTIES IN WCET ANALYSIS FOR MULTI-CORE CHIPS WITH SHARED
L2 CACHES: In a multi-core processor, each core typically has private L1 instruction and data caches. The L2 (and/or L3) caches, however, can either be private or shared. While private L2 caches are more time-predictable in the sense that there are no inter-core L2 cache conflicts, each core can only exploit limited cache space. Due to the great impact of the L2 cache hit rate on the performance of multi-core processors [Liu et al. 2004; Chang and Sohi 2006], private L2 caches may have worse average-case performance than shared L2 caches with the same total size, because each core with a shared L2 cache can possibly make use of the aggregate L2 cache space more efficiently. Moreover, the shared L2 cache architecture makes it easier for multiple cooperative threads to share instructions, data and the precious memory bandwidth to maximize performance [Tian and Shih 2011]. Therefore, in this paper, we focus on studying the WCET analysis of multi-core processors with shared L2 caches (by contrast, the WCET analysis for multi-core chips with private L2 caches is a relatively less challenging problem, since it does not need to consider the inter-core interferences in the shared cache).
2.1 A Dual-Core Processor with a Shared L2 Cache and Our Assumption
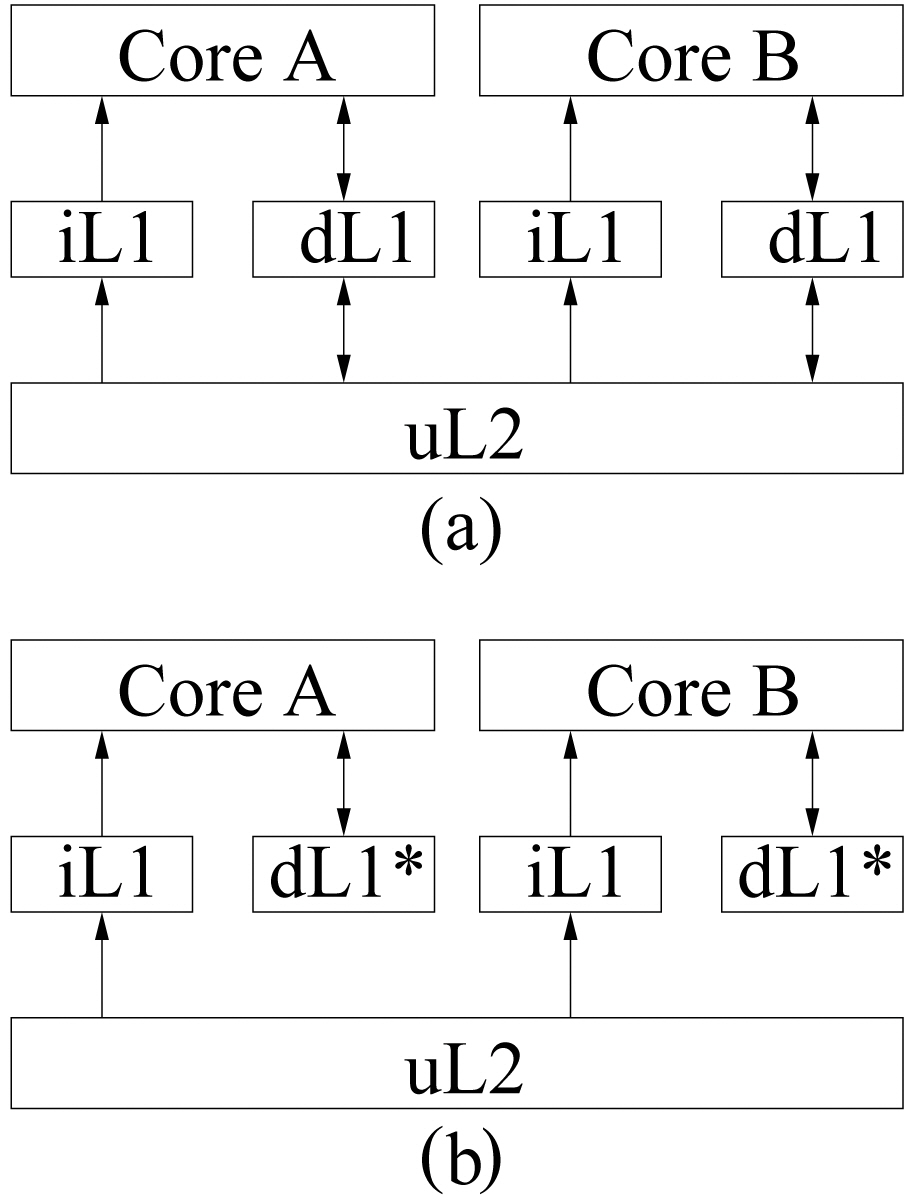
Without losing generality, we assume a dual-core processor with two levels of cache memories, and the proposed static analysis approach can be easily extended to multicore processors with a multi-level memory hierarchy. Figure 1(a) shows a typical dualcore processor, where each core has private L1 instruction and data caches, and shares a unified L2 cache. Since this work focuses on analyzing the inter-thread interferences caused by instruction streams (note that we plan to analyze the worst-case interthread data interferences in our future work), we assume that the L1 data cache in each core is perfect (i.e., no L1 data cache misses so that the instruction accesses to L2 are not affected by data accesses). Specifically, the assumed dual-core architecture is depicted in Figure 1(b), where each core has its own L1 instruction cache and a perfect L1 data cache (i.e., dL1*), and shares the L2 cache.
Also, we assume that two threads consisting of a real-time thread (RT) and a non real-time thread (NRT) are simultaneously running on these two cores, and our task is to safely and accurately estimate the WCET of the real-time thread (assuming nonpreemptive execution)3 by taking into account the possible L2 cache interferences from the non-real-time thread. It should be noted; however, that our work is also effective for two RTs running on a dual-core, where the second RT is just treated as a NRT in our analysis.
2.2 Timing Anomalies in Multi-Core Computing
In a multi-core processor with a shared L2 cache, the data and instructions needed by different cores may be mapped to the same cache blocks in the shared L2 cache, thus leading to inter-core (or inter-thread) cache conflicts. Since the L2 miss latency is typically very high, these inter-thread L2 cache conflicts may greatly impact the performance of each thread, resulting in large performance variation and thus worsening the WCET of each thread. Due to the inter-thread cache conflicts, the WCET analysis of a single task running on a particular core of a multi-core processor has to consider other threads that are executed in other cores on the same processor; otherwise, the WCET analysis of this task is likely to be unsafe.
The inter-thread cache conflicts in multi-core processors with shared cache memories can lead to timing anomalies. Timing anomalies were first discovered in out-of-order superscalar processors by Lundqvist and Stenstrom [1999b], where the worst-case execution time does not necessarily relate to the worst-case behavior. For instance, Lundqvist and Stenstrom [1999b] found that a cache miss in a dynamically-scheduled processor may result in a shorter execution time than a cache hit, which is counterintuitive. Similarly, we find that in a multi-core processor with a shared L2 cache, the worst-case behavior of a single thread does not necessarily lead to the worst-case execution time of that thread, because of the inter-thread cache conflicts.
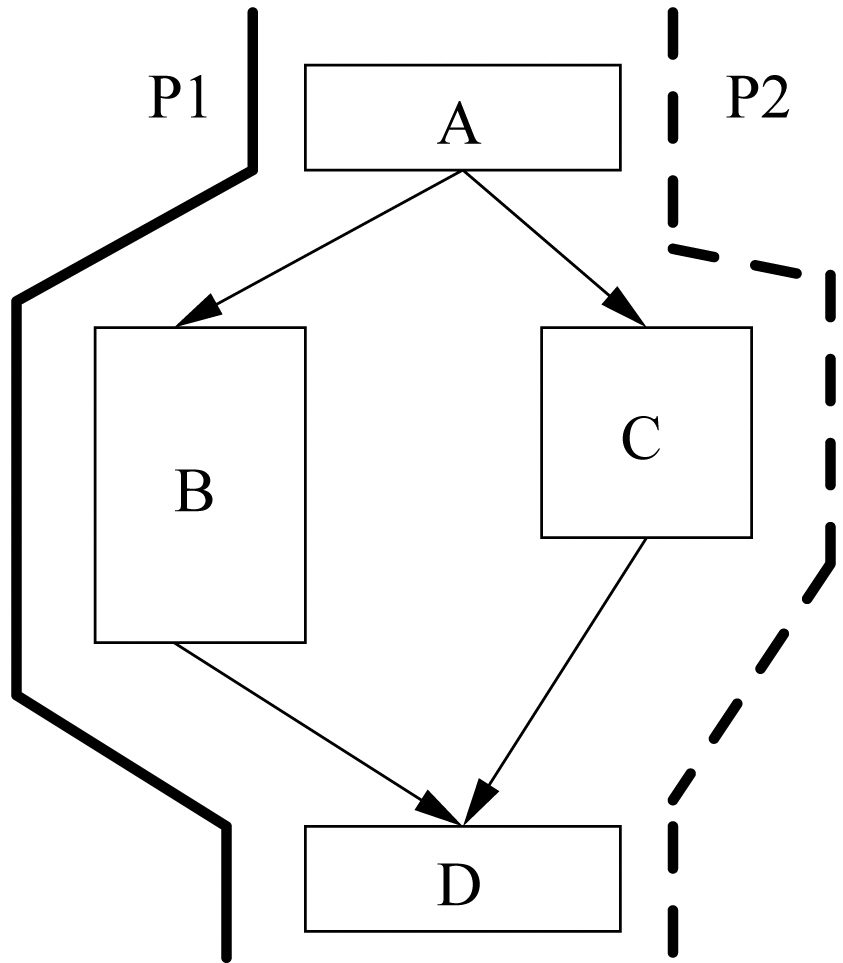
For example, Figure 2 shows the control flow graph of a code segment, which contains two paths:
Because of the timing anomalies in multi-core processors, the WCET analysis of each thread running on each core cannot be performed independently, which can significantly increase the complexity of the timing analysis. In particular, although current timing analysis techniques [Wilhelm et al. 2008] can reasonably bound the performance of a single-core processor, they cannot be easily extended to compute the worst-case performance of each thread running on a multi-core processor. For instance, in Figure 2, while we can use existing single-core WCET analysis techniques [Wilhelm et al.2008] to obtain the worst-case path, i.e.,
1This submission is based on our conference paper entitled “WCET Analysis for Multi-Core Processors with Shared L2 Instruction Caches”, which is published in the 14th IEEE Real-Time and Embedded Technology and Applications Symposium (RTAS), 2008. 2It should be noted that this paper does not solve the full problem of WCET analysis for multi-core chips. However, we believe we have made an important step by reasonably bounding the worst-case shared multi-core cache performance due to instruction accesses. 3It should be noted that this paper focuses on analyzing the WCET of a single real-time task running on a dual-core processor, thus the study of the effects of context switching within a single core and/or across multiple cores falls out of the scope of this paper.
We propose a WCET analysis approach for multi-core processors with shared L2 instruction caches in three major steps, including cache analysis, pipeline analysis and path analysis. Our analysis is built upon extending a single-core timing analysis tool called Chronos [Chronos n.d.], which uses IPET [Li and Malik 1995; Li et al. 1996] to calculate WCET. In this section, we first introduce the static cache analysis to bound the worst-case L2 instruction misses by considering the inter-core instruction interferences in subsection 3.1. Then, we explain the pipeline analysis and path analysis in subsection 3.2 and subsection 3.3, respectively.
3.1 Static Analysis of Inter-Core Instruction Interferences in the Shared L2 Instruction
Cache: The most difficult problem of the multi-core WCET analysis is to reasonably bound the worst-case inter-core interferences in the shared L2 caches. The inter-core L2 instruction interferences depend on several factors, including (1) the instruction addresses of the L2 accesses of each thread, (2) which cache block these instructions may be mapped to, and (3)
identify the worst-case inter-core instruction interferences by distinguishing instructions that are in loops from those instructions not in loops (i.e., used at most once).
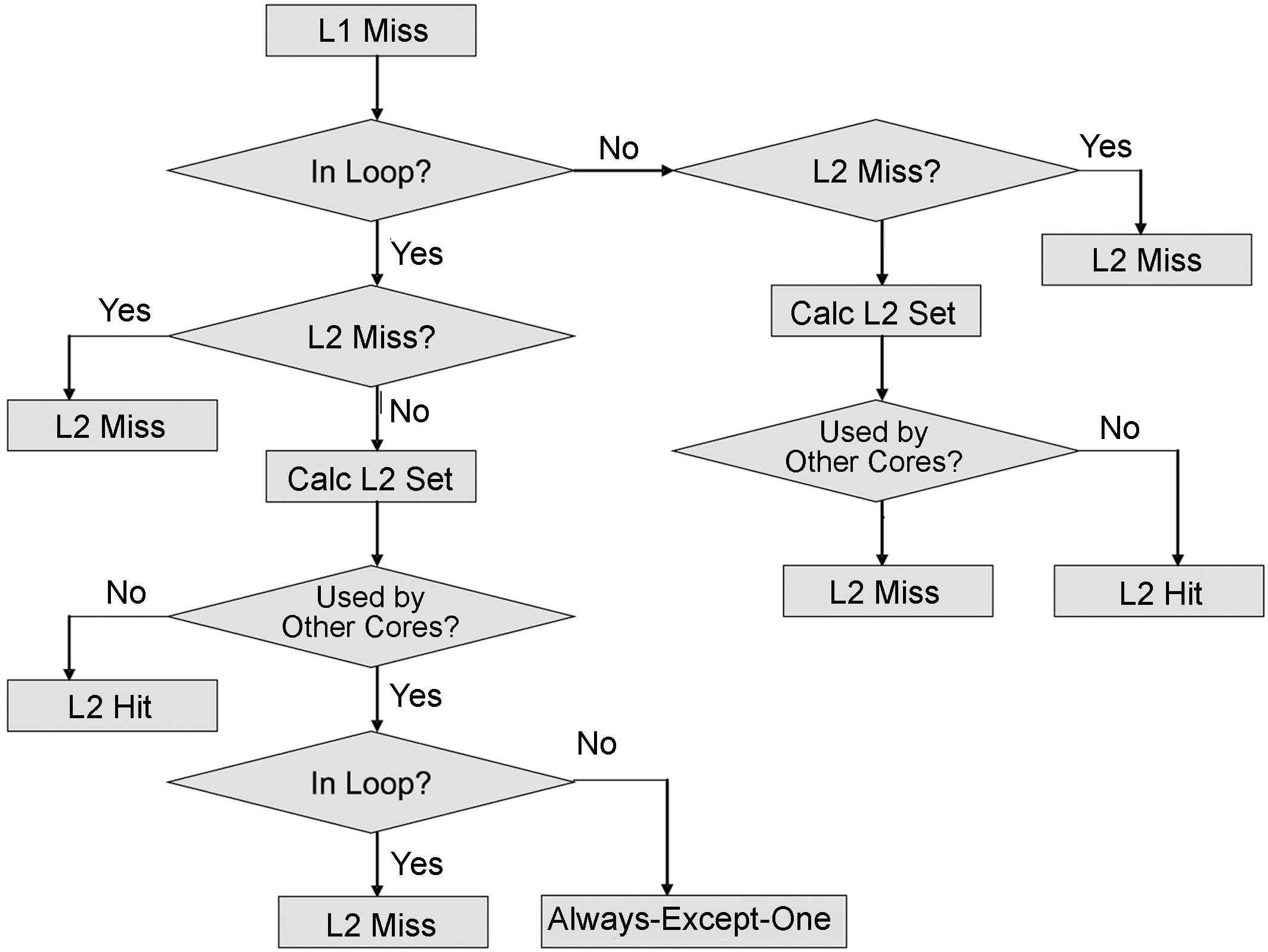
Our approach to estimate the worst-case inter-core instruction interference is shown in Figure 3, which works on each basic block level. As can be seen, when a L1 cache miss is determined (by using the cache static analysis proposed by Ferdinand and Wilhelm [1999]), this information is used as the input to determine the worst-case number of L2 misses. Specifically, when there is a L1 cache miss, we first check whether or not this miss happens in a loop. If this miss is not in the loop, then we determine whether or not it is a L2 miss. If it is not a L2 miss but a L2 hit, then we calculate its cache set number and the conflict set due to L2 accesses from other core(s). If another core may use this set during its execution time, then this L2 hit becomes a L2 miss (in the worst-case). Otherwise, it is still a L2 hit (i.e., “always hit” [Ferdinand and Wilhelm 1999] in the shared L2 cache).
Another situation is when a L1 miss occurs in a loop, as can be seen from Figure 3. If this L1 miss hit is in L2, then we need to determine whether or not this set is used by other cores and whether or not it is used in a loop. If this cache set is used by other cores and at the same time used in a loop, then this L2 hit is classified as a L2 miss. However, if this cache set is used by another core but is accessed by instructions not in loops, then this L2 hit becomes “always-except-one hits”. Otherwise, it is identified as a L2 miss.
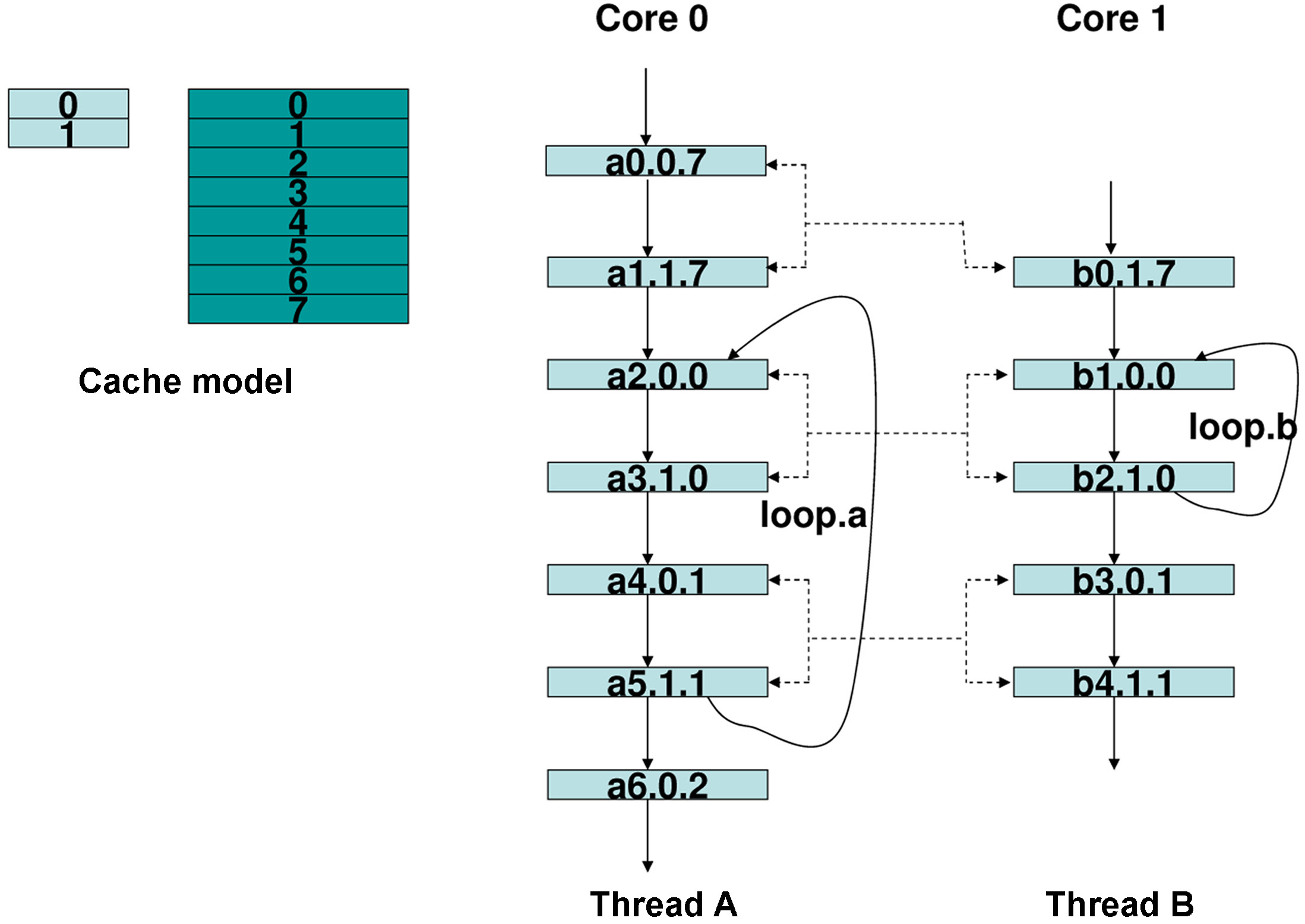
For instance, Figure 4 shows an example to illustrate our approach to bounding the worst-case shared L2 instruction cache performance by considering the inter-core interferences. As can be seen in Figure 4, without loss of generality, we assume that two threads, A and B, are running in a dual-core processor. In this processor, core 0 is time-sensitive and is running thread A; core 1 is not time-sensitive and is running thread B. The control flow graph of two threads is also given in Figure 4. The cache model we use is shown in Figure 4, in which L1 cache has 2 sets and each set can
hold 1 instruction, and L2 cache has 8 sets and each set can hold 2 instructions. Each instruction in Figure 4 is labeled as follows. The starting letter is the affiliated thread number. The number immediately following this letter is the number of this instruction. Then, the next number is the set number of the L1 cache. The last number indicates the set number of the L2 cache. For instance, b2.1.0 means that this is the 2nd instruction in thread B, which refers to set 1 of the L1 cache and set 0 of the L2 cache.
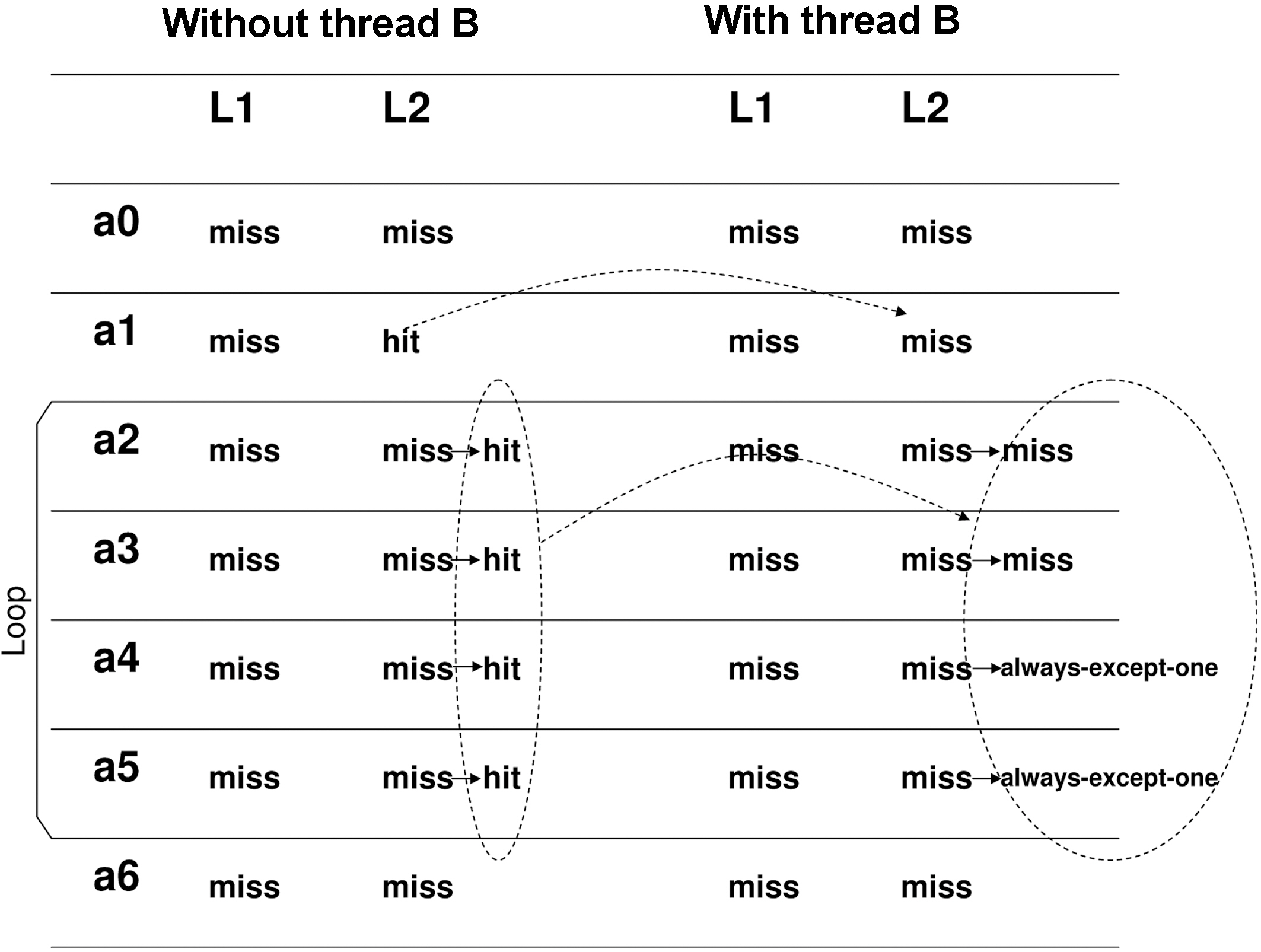
The status of each instruction with and without considering inter-core interferences is shown in Figure 5. For instance, without considering thread B, instruction a0.0.7 is a cold miss of L1 in set 0 and a cold miss of L2 in set 7. After that instruction, a1.1.7 should only suffer L1 miss, since it uses set 1 in the L1 cache and set 7 in the L2 cache. However, if we consider thread B that is concurrently running in core 1, then instruction b0.1.7 may use set 7 of L2 cache too. Thus it may happen that when core 0 finishes instruction a0 but before executing instruction a1, core 1 starts to run instruction b0. In this case, contents in set 7 of the L2 cache will be evicted by core 1. Thus, the status of instruction a.1.1.7 is changed to L2 cache miss in the worst case.
Figure 5 also illustrates how to exploit the loop information to categorize the status of each instruction. For example, loop.a in thread A contains 4 instructions, i.e., a2.0.0, a3.1.0, a4.0.1 and a5.1.1. As can be seen, a2 and a4 conflict with each other in the L1 instruction cache, and so do a3 and a5. However, their references to L2 have no conflicts. During each iteration of loop.a, core 0 needs to fetch these 4 instructions from the L2 cache. Therefore, without considering thread B, the number of L2 cache misses of thread A is 2 at the first iteration and becomes 0 for the subsequent iterations. However, if we take thread B into consideration, as can be seen in Figure 4, then in the worst-case, the alternative running of instructions (a2, a3) and (b1, b2) will lead to two extra L2 cache misses when accessing a2 and a3 from the L2 cache. In contrast, since instructions a4 and a5 only interfere with instructions b3 and b4, which are not in any loop of thread B, their status becomes “always-except-one hits.”
For each core in a multi-core processor, the number of L1 instruction cache misses can be easily obtained by using static analysis techniques for instruction caches [Ferdinand and Wilhelm 1999]. By using the algorithm depicted in Figure 3, we can statically categorize the L2 instruction accesses for each basic block by considering the possible inter-core interferences in the shared L2 cache, which are then used to compute the worst-case number of L2 instruction misses for the program (i.e., the real-time thread) by using the Integer Linear Programming (ILP) equation as shown in Equation 1.
In Equation 1,
is the number of misses caused by “always-except-one hits”, which is only determined by the execution of basic block
As aforementioned, the pipeline analysis, path analysis and WCET calculation in our approach are built upon the IPET method [Li and Malik 1995; Li et al. 1996]. The static analysis of both L1 and L2 caches provides the basis for pipeline analysis to determine the worst-case latency of each instruction at different pipeline stages, as depicted in Figure 6. For any L2 instruction access (which obviously must be a L1 miss), the pipeline latency will be updated based on its categorization by considering possible conflicts from other co-running threads. As can be seen from Figure 6, function
Based on pipeline analysis, the cost of each basic block in terms of the number of execution cycles can be determined, which is used in the objective function given in (2). In this function,
Malik 1995; Li et al. 1996].
The path analysis determines possible paths of a program based on the control flow constraints. As shown in equation (3),
Finally, by putting together equations (1), (2) and (3), the WCET of the real-time thread can be calculated by using an ILP solver.
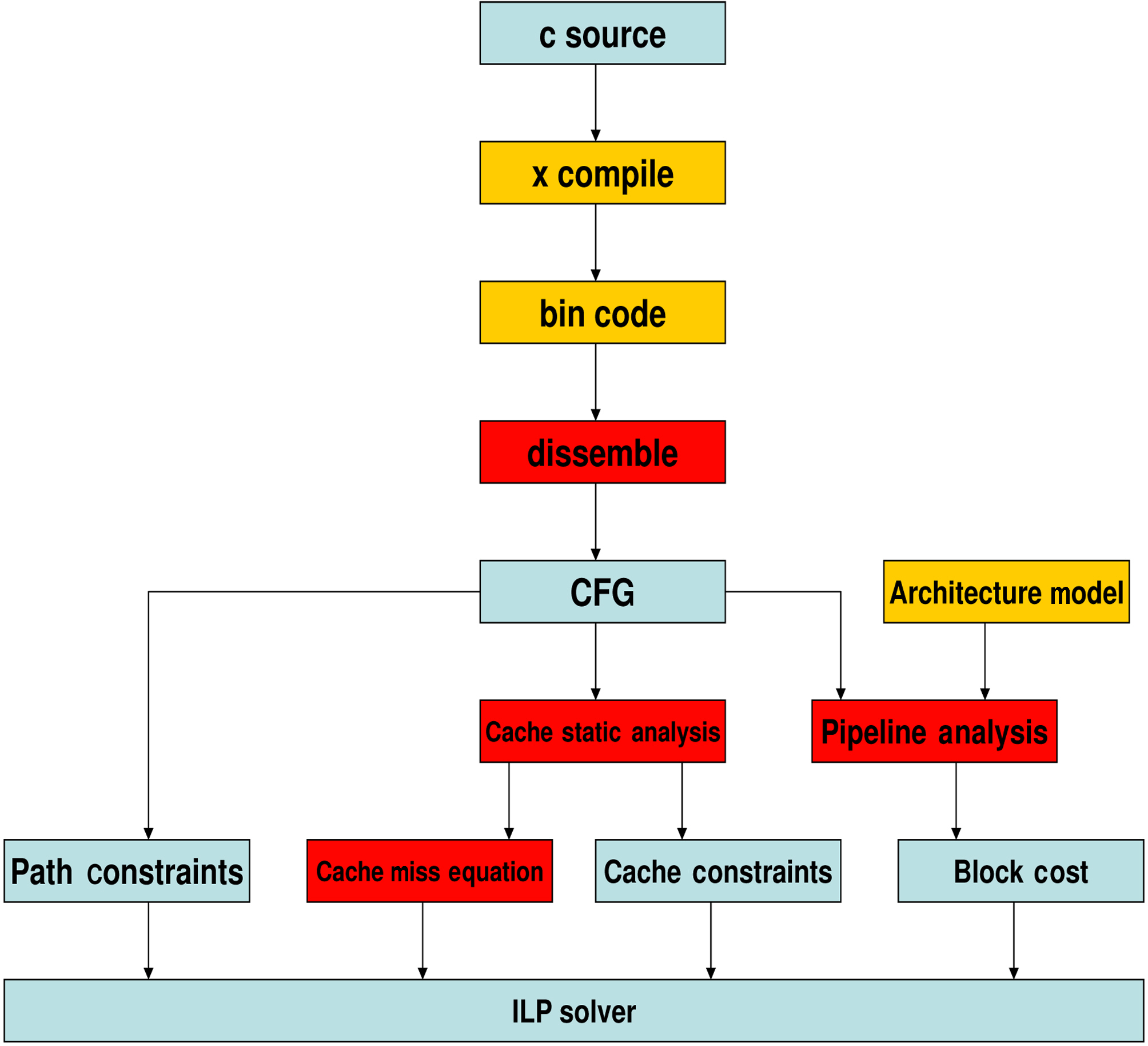
The WCET analysis for multi-core processors is based on extending Chronos timing analysis tool [Chronos n.d.]. Chronos is originally a single core WCET analysis tool, which targets SimpleScalar architecture. We have extended it to implement the proposed inter-core cache static analysis and pipeline analysis for multi-core processors, as is shown in Figure 7. We use gcc to compile two threads (i.e., a real-time thread and a non-real-time thread) into ELF format targeting MIPS R3000 architecture, which can be run on SESC simulator [Renau 2007] to obtain simulated performance. Since Chronos [Chronos n.d.] originally targets SimpleScalar binary code, which is based on COFF format, the front end of Chronos has been retargeted to support SESC binary code based on ELF format, which has been implemented in the dissembling stage in Figure 7. After disassembling the binary code, the control flow graph (CFG) of each individual
[Table 1.] Configurations of the dual-core chip memory hierarchy.

Configurations of the dual-core chip memory hierarchy.
procedure is constructed. Then, Chronos [Chronos n.d.] translates the CFG into
To compare the worst-case performance with the average-case performance (i.e., the simulated performance based on typical inputs), we use SESC simulator [Renau 2007] to simulate a dual-core processor, in which each core is a 4-issue superscalar processor with 5 pipeline stages. The important parameters of the dual-core memory hierarchy are given in Table I. The benchmarks are selected from Malardalen real-time benchmarks [Mal 2007].
5.1 Observed and Estimated Worst-Case Performance Results
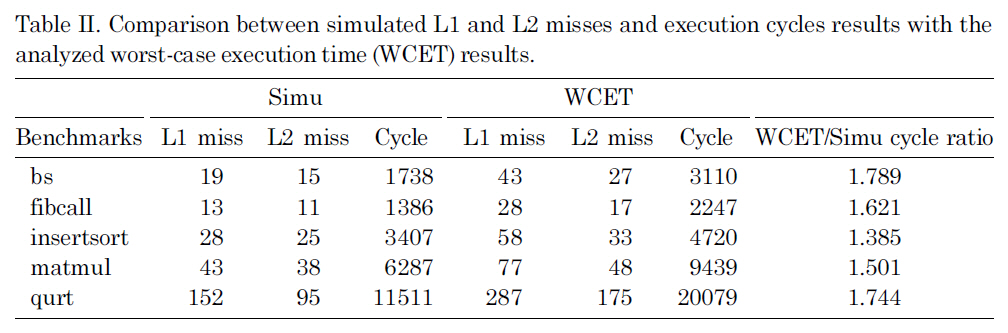
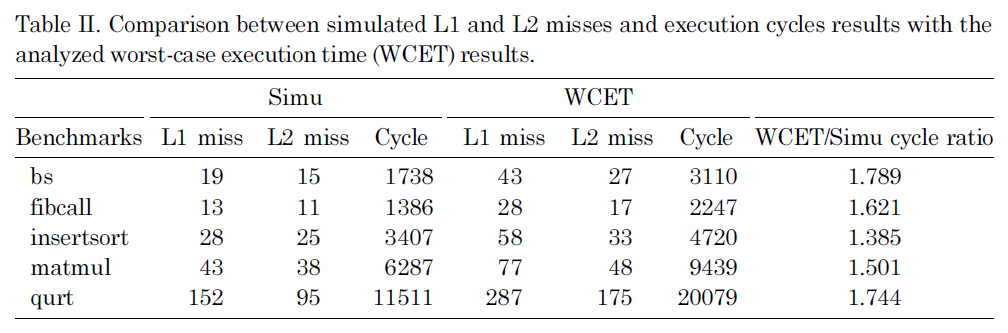
Table II compares the execution cycles, the number of L1 misses and the number of L2 misses between the observed results through simulation and the estimated results through WCET analysis. In these experiments, we choose five real-time benchmarks (i.e., bs, fibcall, insertsort, matmul and qurt) from Malardalen benchmark suite [Mal 2007], and another benchmark adpcm-test is used as a non-real-time benchmark, which is simultaneously executed with each real-time benchmark on the dual-core processor. Since our concern is to obtain the worst-case performance for the real-time benchmarks, Table II only shows the simulated and analyzed results for those five real-time benchmarks, by taking into account the L2 cache interferences from adpcmtest.
As can be seen in the last column of Table II, the estimated WCET is not too far from the observed WCET for most benchmarks. The overestimation in our WCET analysis mainly comes from three sources. First, the worst-case execution counts of basic blocks estimated through ILP calculation are often larger than the actual execution counts during simulation. Second, the cache static analysis approach [Ferdinand and Wilhelm 1999] used for the L1 instruction cache analysis is very conservative. As can be seen in Table II, the estimated number of L1 misses is much larger than the simulated number of L1 misses that will not only directly increase the
Comparison between simulated L1 and L2 misses and execution cycles results with the analyzed worst-case execution time (WCET) results.
estimated WCET, but also lead to overestimation of L2 misses. Third, our static L2 instruction miss analysis does not consider the timing of interferences from other threads (i.e.,
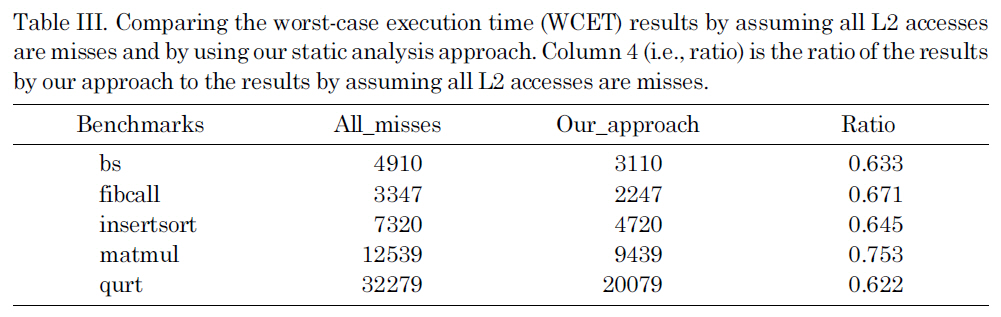
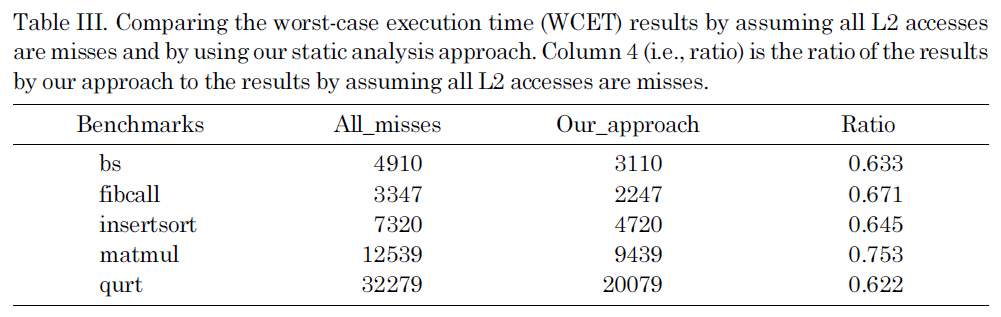
Due to the difficulty of analyzing the inter-thread cache interferences and bounding the worst-case performance of the shared L2 caches in a multi-core chip, an obvious solution is to simply disable the shared L2 cache (i.e., assuming that every access to the L2 cache is a miss), which provides the reference values that we compare the results of our analysis to. Table III compares the estimated WCET by assuming all L2 accesses are misses with the WCET estimated by our approach. As we can see, by statically bounding the L2 cache instruction interferences, the estimated WCET is much smaller than the results by assuming all the L2 accesses are misses, indicating the enhanced tightness of WCET analysis. This improvement is because our approach can reasonably estimate the upper bound of the L2 instruction misses by considering the inter-core interferences, which can be seen from Table II by comparing the simulated number of L2 misses (i.e., column three) with the estimated number of L2 misses (i.e., column six).
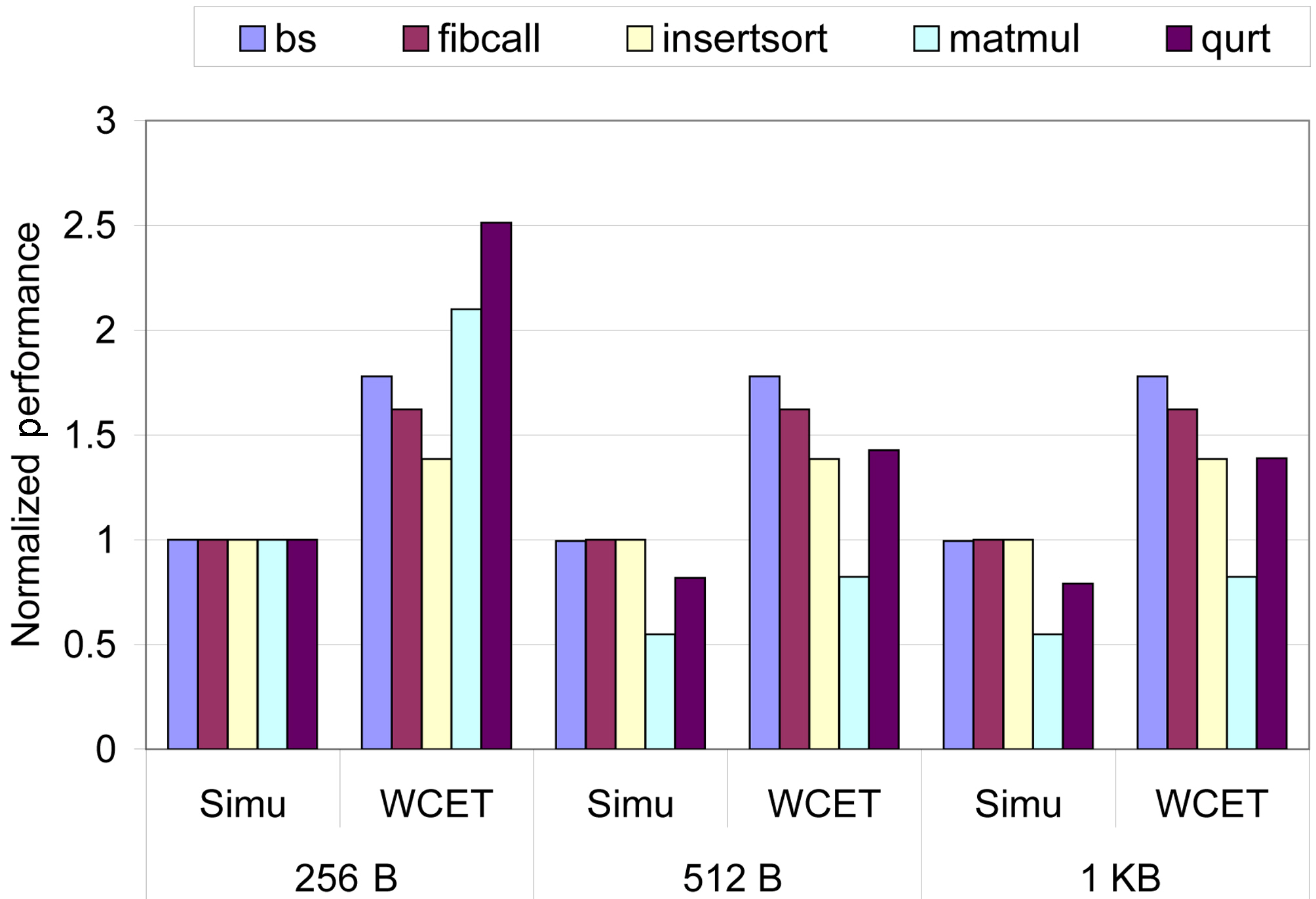
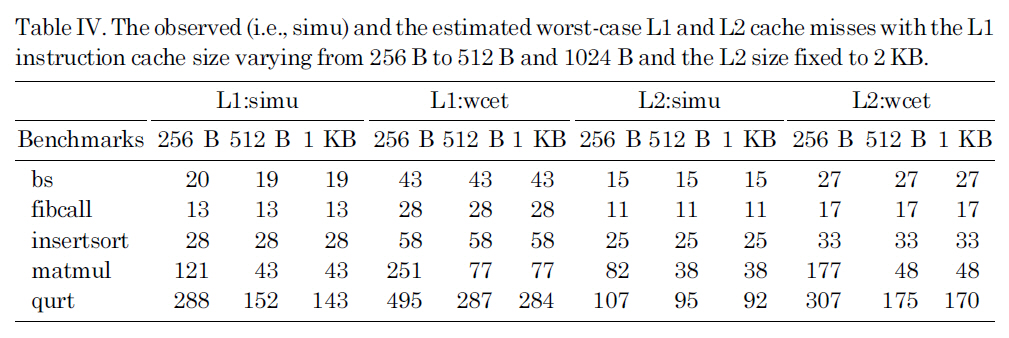
Figure 8 compares the observed (i.e., simu) WCET and the estimated WCET for multicore processors with the L1 instruction cache size varying from 256 B to 512 B and 1 KB, while the L2 cache size is fixed to 2 KB, which are normalized with the observed WCET with the 256 B L1 instruction cache. We find that for small benchmarks such as bs, fibcall and insertsort, increasing the L1 cache size has no impact on both the observed and estimated WCET. However, for other benchmarks including matmul and qurt, the observed WCET is decreased as the size of the L1 instruction cache increases, due to the reduction of cache misses. For all these three L1 instruction cache configurations, we find that the proposed static analysis approach can safely bound the worst-case execution cycles. Also, we observe that the estimated WCET is reasonably tight for 512 B and 1 KB instruction caches; however, the overestimation becomes larger with a 256 B L1 instruction cache, because of the increased L1 and
Comparing the worst-case execution time (WCET) results by assuming all L2 accesses are misses and by using our static analysis approach. Column 4 (i.e. ratio) is the ratio of the results by our approach to the results by assuming all L2 accesses are misses.
L2 cache misses and more inter-core cache conflicts.
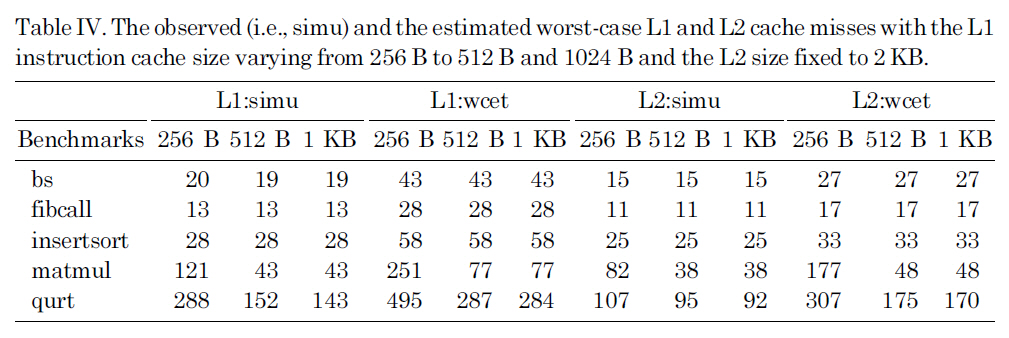
Table IV lists observed (i.e., simu) and the estimated worst-case L1 and L2 cache misses with the L1 instruction cache size varying from 256 B to 512 B and 1024 B and the L2 size fixed to 2 KB. The results in this table can clearly explain the performance change in Figure 8. More specifically, as we can see in Table IV, for bs, fibcall and insertsort, increasing the L1 instruction cache size has little or no
The observed (i.e. simu) and the estimated worst-case L1 and L2 cache misses with the L1 instruction cache size varying from 256 B to 512 B and 1024 B and the L2 size fixed to 2 KB.
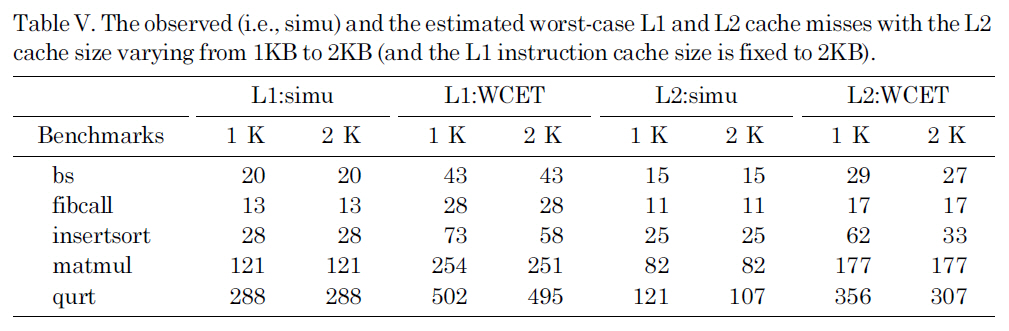
The observed (i.e. simu) and the estimated worst-case L1 and L2 cache misses with the L2 cache size varying from 1KB to 2KB (and the L1 instruction cache size is fixed to 2KB).
impact on the L1 and L2 instruction cache misses. As a result, both the simulated and estimated WCET for these benchmarks remain stable with different L1 instruction caches. By comparison, for matmul and qurt, as the L1 instruction cache size is increased from 256B to 512B, the number of L1 instruction cache misses is significantly reduced, leading to substantial reduction in the L2 cache misses and WCET. For all different instruction cache sizes, the experimental results indicate that the proposed approach can safely predict the upper bound of the L1 and L2 cache misses.
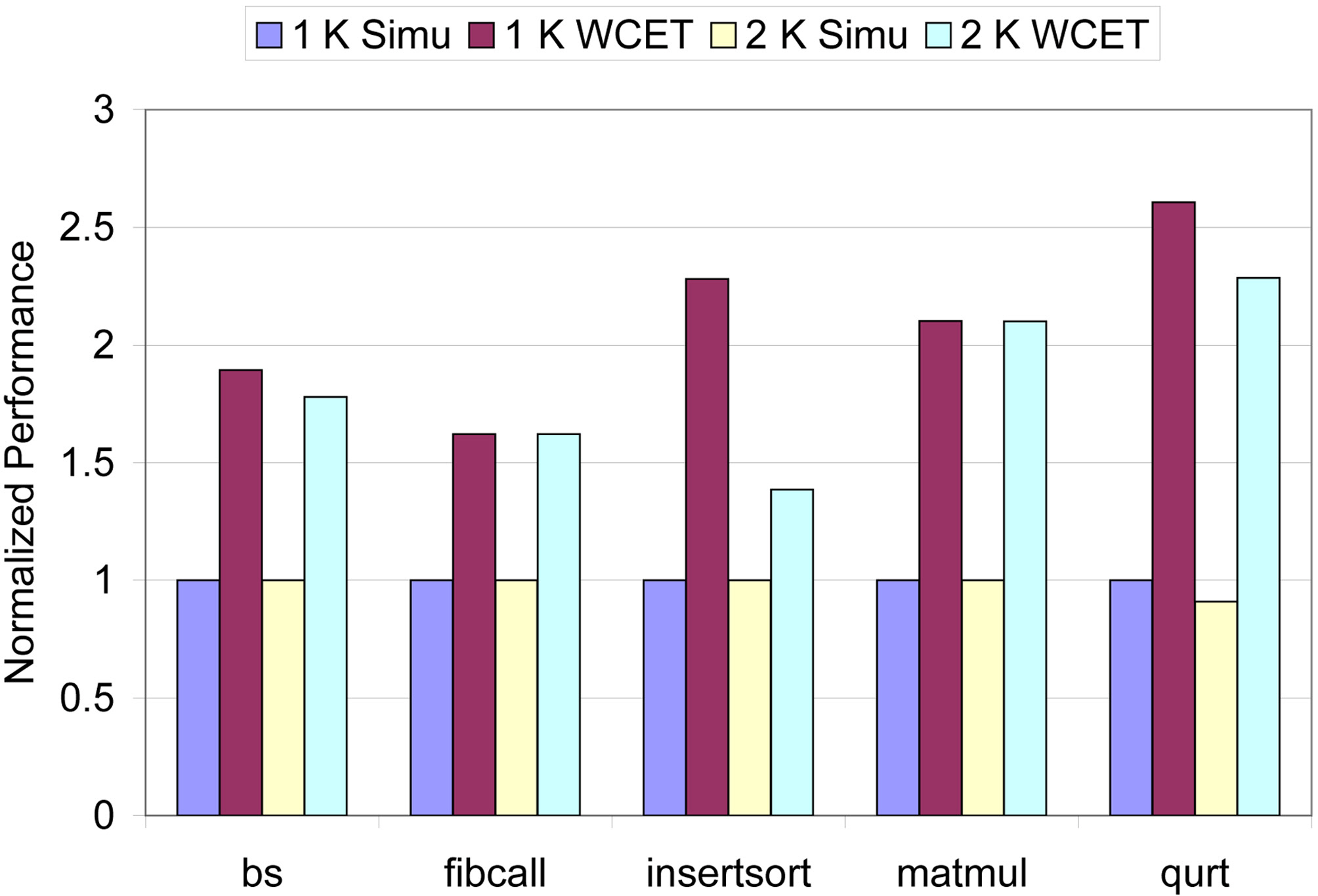
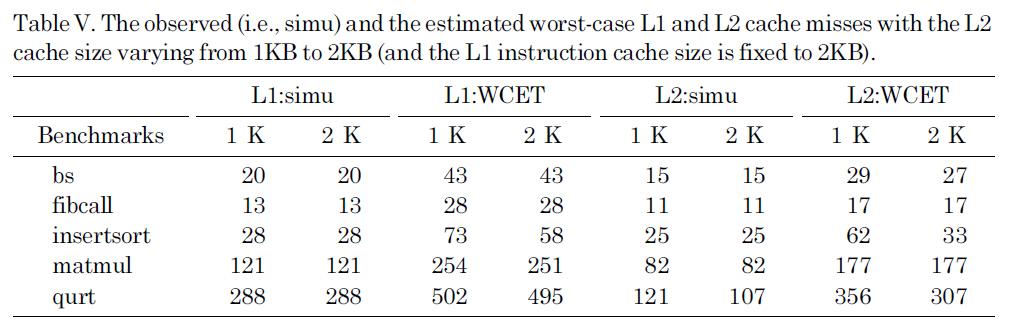
Our next sensitivity study focuses on the L2 cache. Figure 9 shows the observed (i.e.,simu) and the estimated WCET with the size of the L2 cache varying from 1 KB to 2 KB and with the L1 instruction cache size fixed to 256 B, which are normalized with the observed WCET with the 1 KB L2 cache. The corresponding L1 and L2 cache misses are listed in Table V. As we can see in Figure 9, the proposed approach can safely estimate the WCET with reasonable accuracy for both 1 KB and 2 KB L2 caches. As can be seen in Table V, increasing the L2 cache size substantially reduces the L2 cache misses for qurt, while having no impact on the L1 and L2 cache misses for other benchmarks. As a result, as depicted in Figure 9, both the observed and estimated WCET of qurt decrease as the L2 cache size increases from 1KB to 2KB, while for other benchmarks, the impact of increasing the L2 cache size from 1 KB to 2 KB is insignificant.
This paper presents a novel and effective approach to bounding the worst-case performance of multi-core chips with shared L2 instruction caches. To accurately estimate the runtime inter-core instruction interferences between different threads, we propose to categorize L2 accesses by exploiting the program control flow information (i.e., instructions in loops vs. instructions not in loops). The cache analysis results (including the shared L2 instruction cache) are then integrated with the pipeline analysis and path analysis through ILP equations to obtain the worst-case execution cycles. Our experiments indicate that the proposed approach can reasonably bound the worst-case performance of threads running on multi-core processors by considering the inter-thread interferences due to instruction accesses to the shared L2 cache by different co-running threads. Also, compared with the approach by simply disabling the L2 caches to avoid interferences, our approach can provide much better worst-case performance for real-time benchmarks.
In our future work, we plan to further enhance the tightness of the static analysis for shared L2 caches. Specifically, we would like to take into account the time ranges of interferences to minimize the overestimation of worst-case instruction interferences between threads. Also, while this paper focuses on analyzing direct-mapped caches, we intend to study multi-core WCET analysis for the set-associative caches as well. In addition, we plan to investigate shared data cache analysis for multi-core chips that can then be integrated with this work to fully analyze the worst-case performance for multi-core processors with shared cache memories.