The joint transform correlator (JTC) has shown remarkable achievements for real time pattern recognition and target tracking applications. Especially for pattern recognition, it can be applied to facial appearance, fingerprints, handwriting,and character recognition [1-6]. The typical advantages of the JTC are that it uses a type of real time optical system which quantitatively analyzes and compares the images by measuring a correlation peak and peak signal to-noise ratio(PSNR). This kind of optical pattern recognition system goes through a double random encryption and double-encryption process using the JTC method. However, it also has drawbacks in that it is sensitive to rotation or shifting of images.Moreover, it has some problems with nonlinearity of the optical components such as a digital camera, and with weak correlation discrimination caused by noise. Recently many methods for solving such problems in the JTC have been studied. Among them, the nonlinear joint transform correlator (NJTC), which can solve the problem of the nonlinear components in the JTC system, may be the most typical [7-9]. In addition, an essential technique in pattern recognition and identification is that of finding an accurate recognition method when the input images are rotated in angle and translated in position [10-11]. In spite of such efforts, weak correlation discrimination and noise problems still remain. Such kinds of weak correlation discrimination and noise problems originate from the interference fringes constructed with a Fourier transformed reference and a sample image in the Fourier transform plane. Some attempts to improve the discrimination ratio as well as the optical efficiency have been made in the spatial domain or in the frequency domain. However, most attempts are divided into two groups, one group uses an intensity or a phase threshold and the other group uses some kinds of filtering. Alam successfully applied the synthetic discrimination function(SDF) filter concept to a JTC system and used a Fourier plane image subtraction technique [12-14]. Although this technique successfully improved the correlation peak and reduced the side-lobe noise, it adopts a simple input joint images enhancement using an image normalization and spatial domain iterative filtering process. Thus it has problems finding suitable parameter values to adjust the fringe with a minimum error function, and it needs another liquid crystal display (LCD) in the spatial domain. In order to solve these problems, we [15] have proposed a technique of modifications of the interference fringes by adopting a spectrum domain iterative filtering technique which can find the optimum condition with minimum error for a highly improved PSNR and reduced side-lobe noise. Unlike Alam’s technique, our technique has dealt with fringe-adjustment by inserting an iterative filtering step in the joint power spectrum (JPS) domain to enhance the interference fringe pattern instead of inserting the iterative filter after the input joint images. Although this technique successfully increased the PSNR ratio to reduce the side-lobe noise, it showed rather low correlation peak ratio compared with Alam’s technique [14].

In order to enhance both the correlation peak and the PSNR, we present a new technique of modifications of the interference fringes by introducing a sinusoidal amplitudemodulated iterative filter convolved with the interference fringe in the JPS domain. Experimental results are presented to show that the proposed technique can successfully improve the correlation peaks and the PSNR. In the following section, the proposed new method of fringe-adjusted JTC system and its algorithm, including the sinusoidal amplitude modulated iterative filtering technique, are described in detail. Section III describes simulation results for a pattern recognition enhancement and, finally some comments are contained in the Conclusion.

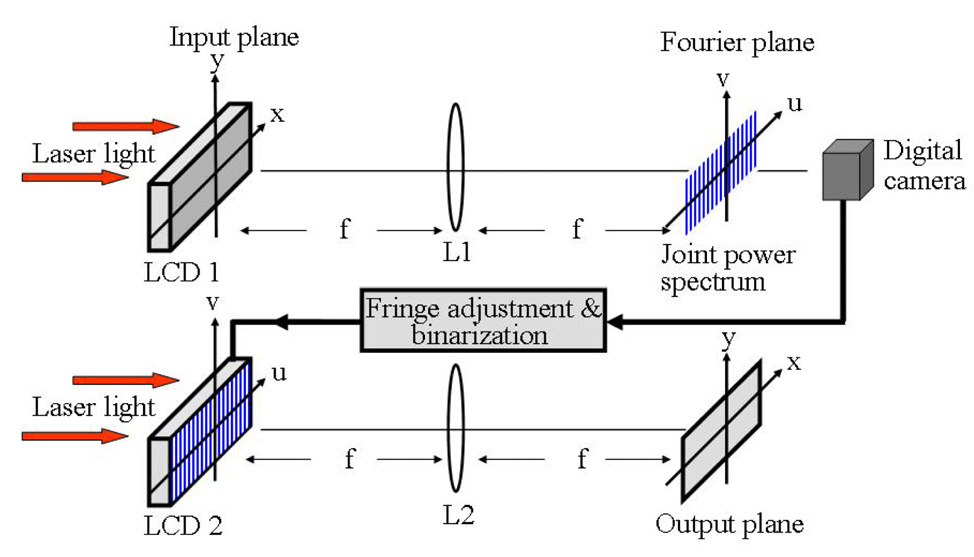
Fig. 1 shows the optical structure of the basic NJTC system which compensates for the nonlinear optical components such as a CCD camera. NJTC uses a two-stage process. In both stages the image of a coherently illuminated input passes through a lens to take its Fourier transform.In the first stage of NJTC the basic operation is to get the information of the Fourier transformed object from the Fourier transform lens L1 onto the Fourier plane. Let us call the reference image (x,y) and the input image s(x,y)and assume that those two inputs are separated by 2x_o.Then, the input joint images g(x,y) can be expressed as

The information acquired on the Fourier plane is shown

as a mutually interfered fringe pattern between the Fourier transformed value R(u,v) of the reference image r(x,y) and the Fourier transformed value S(u,v) of the input image s(x,y). The Fourier transformed signal of the input joint images can be expressed as

The intensity of this interference fringe pattern is called the joint power spectrum (JPS). Therefore, JPS, the intensity of the interfered light acquired with a light detector on the Fourier plane, can be expressed as in Eq. (3)

Here, * is the phase conjugate, u and v are independent spatial frequency variables adjusted in their size by 2π/fλ, λ is the wavelength of input light and f is the focal length of the Fourier transform lens L1. The JPS contains noise and DC components which degrade the correlated signal obtained on the output plane in the second stage. These DC components should be blocked to obtain a well-correlated signal. The blocking of the DC components may be solved by use of a Fourier-plane image-subtraction technique. First,we display the input image at the input-plane SLM of the JTC in the absence of the reference image and record the input-image-only power spectrum. Then we display only the reference image at the input plane to obtain the reference only power spectrum. Both the input-image-only power spectrum and the reference-only power spectrum are then subtracted from the JPS of Eq. (3). This paper also introduces a non-linearity parameter k to compensate the nonlinear component problem caused by elements such as the digital camera. Now, the nonlinear characteristics of the NJTC system are denoted by g(E) where E is the modified JPS excluding the DC terms as shown in Fig. 2. [16]This kind of transfer function adapts the model of Sigmoid function similar to the input-output characteristics of the SLM. Now, Eq. (4) indicates the JPS G'(u,v) excluding the DC terms and including the non-linearity parameter k.

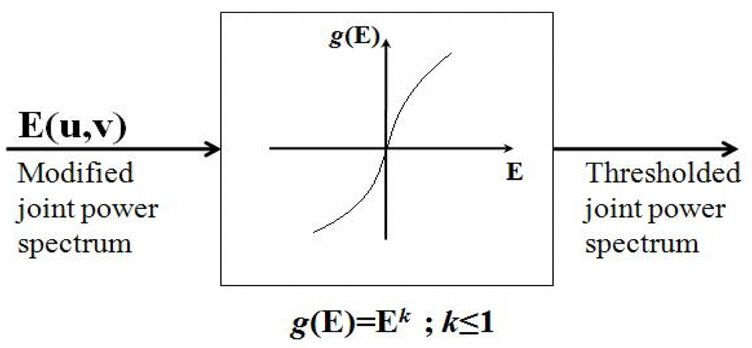
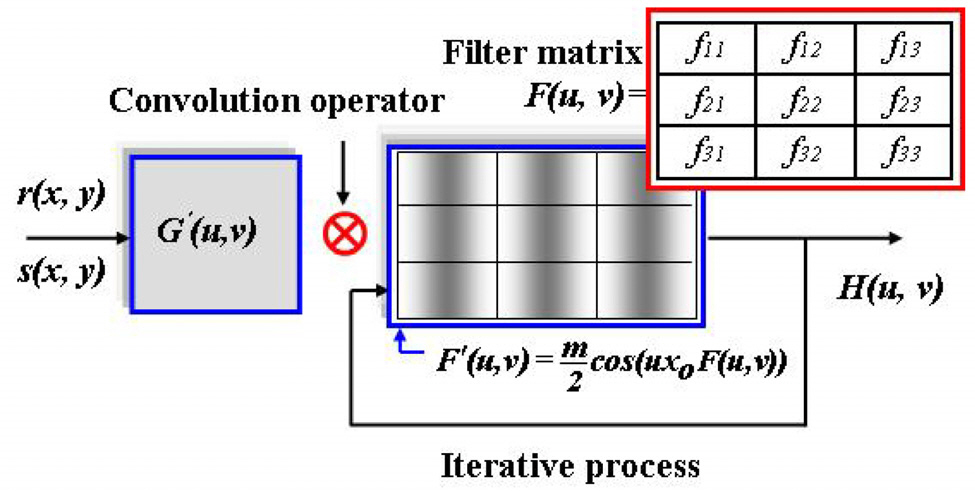
This paper proposes a new technique of modifications of the interference fringes by adopting a sinusoidal amplitude modulated iterative filter in frequency domain. The proposed iterative filter has frequency domain variables and it convolves with the JPS excluding the DC terms,namely G'(u,v), which also has frequency variables. Fig. 3 shows the basic convolution architecture between the input JPS and the sinusoidal amplitude modulated iterative filter.The basic concept of our new sinusoidal amplitude modulated iterative filter originates in the cosine function of the interference fringe pattern in the JPS. The sinusoidal amplitude modulated iterative filter can be expressed using a cosine function as

where m is the magnitude of the modulation. F(u,v) is an elementary filter matrix which can be treated as a weighting value. Mathematically, this process can be expressed as a convolution. Eq. (6) shows the modified JPS of the interference fringe pattern convolved with the iterative filter F'(u,v).

Here, ⊙ denotes convolution. Now, let’s explain the iteration process in more detail. The output H(u,v) shown in Fig. 2 is the result in the training of the iterative process, so the iterative function can be described as Eq. (7).

Here, f_i,j(t) is the elements of the matrix of the elementary filter function which has a size of p×q pixels, f '_i,j'(t) is the cosine amplitude modulated filter function of f_i,j(t), g is the iterative function, and h_m,n(t+1) and h_m,n(t) are the elements of the outputs and inputs of the system, respectively. Here, t is the iteration step. In this iterative process, the initial value of h_m+i, _n+j(t), namely h_m+i, n+j(0), is G'(u,v),and f_i,j(0) is a 3×3 matrix consisting of the value of -1, 0 and +1. In general, the iterative function expressed in Eq.(7) is a nonlinear activation function, so a scalar bias value must be included in this nonlinear JTC. However we already include this nonlinear factor in Eq. (3) and Eq.(4), so we exclude the scalar bias value. In this process,the main goal is to minimize an error function. The error function can be defined by the use of mean square error(MSE) function E as shown in Eq. (8).

Here, H_d(u,v) is the desired output which satisfies with a suitable minimum MSE. The gradient-descent algorithm was used to find the derivation of the error function in order to minimize the MSE [17]. For each iteration step, the filter coefficients are updated as follows.

Here, α represents the iteration rate. Now, the partial derivatives of Eq. (9) can be conveniently computed with the chain rule of calculus as shown in Eq. (10).

The second term in Eq. (10) can easily be computed,because the function c(t) is an explicit function of the coefficients in our iteration, that is

Therefore

The first term in Eq. (10) is called the sensitivity of the error function E, which is calculated by using the following equation.

Here, h_d represents the desired output as shown in Eq. (8).Now, in the second stage the modified JPS H(u,v) is Fourier transformed by the inverse Fourier transform lens L2, and finally a correlated signal from the two signals of the reference and the input image appears on the output plane. The output of the inverse Fourier transform of the modified JPS H(u,v) can be expressed as

Here, ？ is the correlation operator, ？^?1 is the inverse Fourier transform operator. As mentioned in Eq. (5) a is a weighting value obtained from the elementary filter matrix F(u,v) and its iteration process. We can treat a as a weighting value, because F(u,v) is a matrix of 3×3 consisted of the integer value of -1, 0 and +1. Thus, the inverse Fourier transform of the F'(u,v) will have the form of the equation in the fourth line of Eq. (14). The output is adjusted in their size by (λf)².

However, if the cosine amplitude modulated iteration filter process is removed, the output is simply the inverse Fourier transform of G'(u,v). Thus the correlation output can be expressed as

Therefore, Eq. (14) and Eq. (15) show that in the case of using the cosine amplitude modulated iteration filter the correlation peaks can be amplified considerably by a factor of am/2. In the next section, we present the simulated results by using the mathematical model shown in Eq. (14)and Eq. (15).

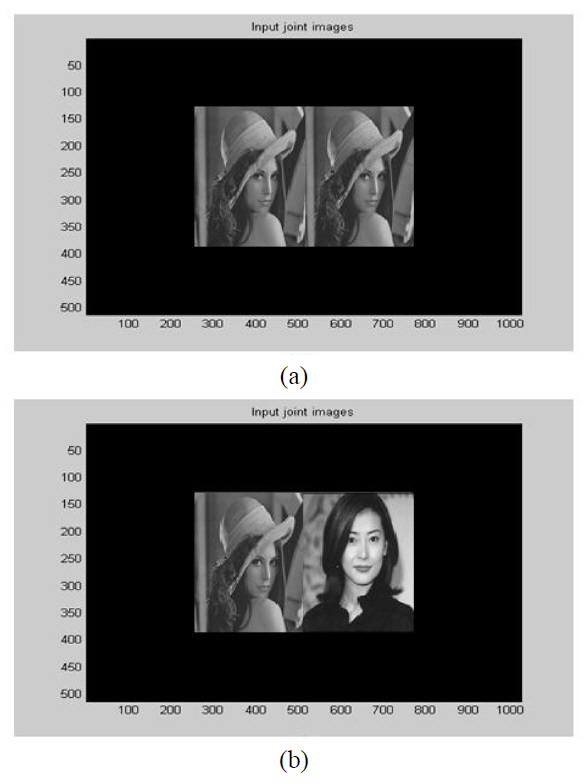
To evaluate the performance of the proposed iterative filter modifying the interference fringe pattern, we prepared 256×256 gray input joint images of a portrait. In Fig. 4,the top image is for a match case and bottom image is for a mismatch case In this paper, we introduced two widely used parameters; the correlation peaks and PSNR. Correlation peaks are the peak magnitudes of the correlated signals. If we let the correlation peaks be 'p(x,y)', then the PSNR can be defined as Eq. (16).

Here, μ represents the mean value, and  represents the standard deviation. Table 1 shows the obtained correlation peak and PSNR of the input joint images for the match and the mismatch case. In particular, Table 1 shows the values of the correlation peak and PSNR obtained using the conventional binary NJTC without the cosine amplitude modulated iterative filter, and with that filter on the spectrum domain. Table 1 indicates that all of the correlation peaks and PSNR increased considerably when the cosine amplitude modulated iterative filter was used. Let us pay attention to the obtained values of the correlation peaks and PSNR,and we can find that the correlation peaks and the PSNR show rapidly increased values when our new cosine amplitude modulated iterative filter was used. First, when we do not use the cosine amplitude modulated iterative filter, the obtained correlation peaks and the PSNR is 2.79×10⁸ and 7.81×10⁵ in the case of the match, respectively, and is 2.23×10⁸ and 1.78×10₅ in the case of the mismatch. Second,when we use the cosine amplitude modulated iterative filter,the obtained correlation peaks and the PSNR is 1.99×10¹¹ and 4.34×10⁷ in the case of the match, respectively, and is 1.82×10¹¹ and 7.00×10⁶ in the case of the mismatch,.

Table 2 shows the ratio of the correlation peaks and PSNR for the cases of adopting the iterative filter processing and for not adopting it. In this paper we classified three types

of the iterative filter convolution processing. All of the obtained values of the ratio shown on Table 2 are for the match case, representatively. The left side of Table 2 is for the case of using Alam’s iterative filter processing[13], the middle of Table 2 is for the case of using our previously presented iterative filter processing [14], and finally the right side of Table 2 is for the case of our new cosine amplitude modulated iterative filter processing.First, for the case of using Alam’s iterative filter in the spatial domain, concerning the correlation peaks, the iterative filter process yields enhanced results that are a maximum of 109.00 times better than those for the case without the iterative filter processing. Now, concerning the PSNR, the iterative filter process yields enhanced results that are a maximum of 15.80 times better than those for the case without the iterative filter processing. Second, for the case of using our previously presented iterative filter in the spectrum domain, concerning the correlation peaks, the iterative filter process yields enhanced results that are a maximum of 10.66 times better than those for the case without the iterative filter processing. Now, concerning the PSNR, the iterative filter process yields enhanced results that are a maximum of 29.79 times better than those for the case without the iterative filter processing. Finally, for the case of using our new cosine amplitude modulated iterative filter processing in the spectrum domain, concerning the correlation peaks, the iterative filter process yields enhanced results that are a maximum of 713.26 times better than those for the case without the iterative filter processing.Now, concerning the PSNR, the iterative filter process yields enhanced results that are a maximum of 55.57 times better than those for the case without the iterative filter processing. Thus, by investigating the results of Table 1 and Table 2, we can say finally that the correlation peaks and the PSNR increased rapidly for the new cosine amplitude modulated iterative filter. In contrast, concerning the efficiency of the discrimination which is the correlation peak ratio between the case of the match and mismatch,Table 1 and Table 2 do not indicate that there is an enhancement by using the cosine amplitude modulated iterative filter. However, concerning the PSNR ratio between the

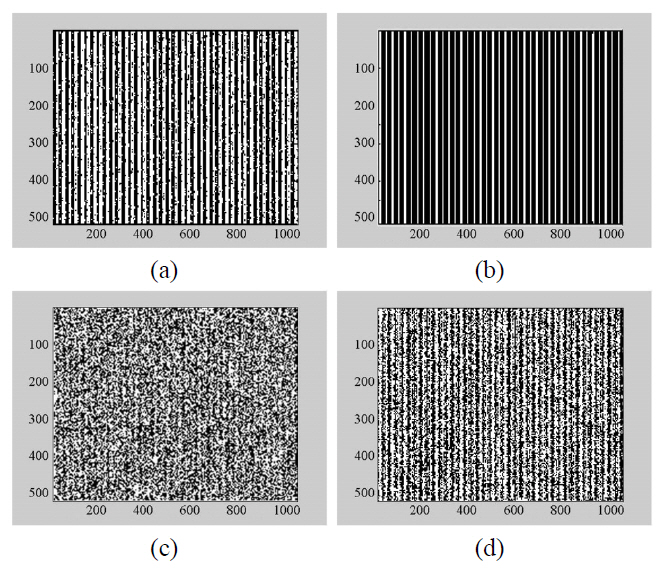
case of the match and mismatch, the results show that there is a considerable enhancement. Thus, we can conclude that the noise contained in the interference fringe pattern is considerably reduced through the cosine amplitude modulated iterative filter convolution processing. This point is very important, so we can say that an ability to determine the match or mismatch in the case of the input images containing some noise or to find an actual image among the clustered images is enhanced considerably. Thus, our results can be efficiently used for tracking an actual image among noisy or clustered images. Fig. 5 shows the interference fringe pattern obtained with the input joint images of the portrait for the cases of adopting the cosine amplitude modulated iterative filter processing and for not adopting it. Fig. 5(a)and Fig. 5(c) are for not adopting it, and Fig. 5(b) and Fig. 5(d) are for adopting it. Fig. 5(a) and 5(b) are for the match case, and Fig. 5(c) and 5(d) are for the mismatch case. Fig. 5 proves the conclusions mentioned above, that

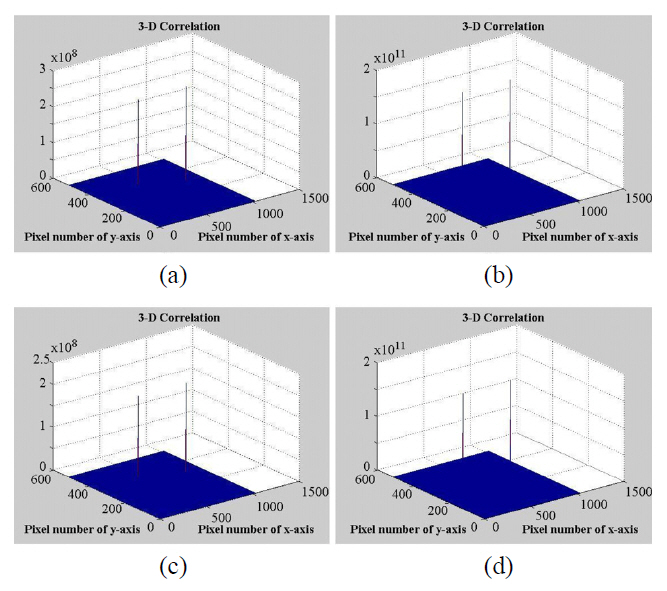
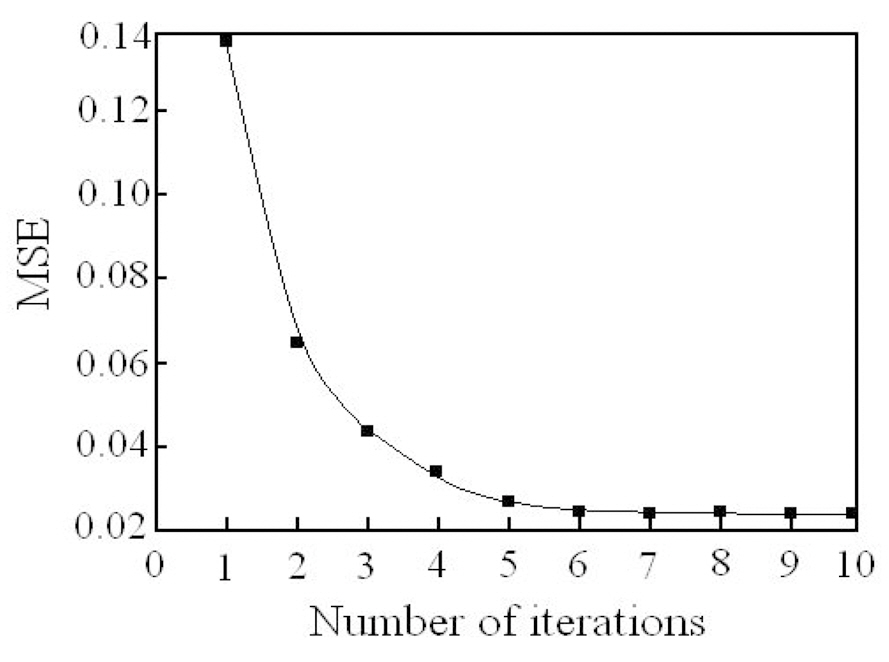
is, the proposed iterative filter convolution process in JPS domain successfully achieved good enhancement of interference fringe shape reducing the noise but increasing the contrast. Fig. 6 shows the three dimensional pictures of the correlation peaks of the input joint images comparing the changes in values without the cosine amplitude modulated iterative filtering and with the iterative filtering process.Fig. 6(a) and Fig. 6(c) are for not adopting it, and Fig.6(b) and Fig. 6(d) are for adopting it. Fig. 6(a) and 6(b)are for the match case, and Fig. 6(c) and 6(d) are for the mismatch case. Fig. 7 shows the error function according to the iteration step.

In this paper, a new technique of modifications of the interference fringes by adopting sinusoidal amplitude modulated iterative filter processing instead of simple iterative filter processing was presented. The proposed sinusoidal amplitude modulated iterative filter has frequency domain variables and it convolves with the JPS excluding the DC terms.Experimental results showed that the proposed technique can successfully increase the correlation peaks and PSNR compared with other techniques.