In long-period fiber gratings (LPFG), a fundamental core mode and the multiple cladding modes are coupled,which all propagate in the same (forward) direction. Due to unique features of low insertion loss, low back-reflection and excellent polarization insensitivity, LPFGs have attracted great interest in the optical communications and sensor applications [1, 2]. Some researchers have studied the manufacture of the core mode blocker [3, 4], band pass filter using the core mode blocker [5-7], and tunable bandpass filter using coil heater [8, 9].

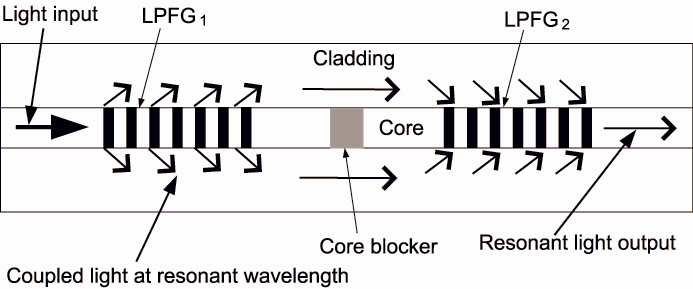
The core mode blocker is a device to block off the propagated light in the core, and pass the propagated light in the cladding. Some researchers have developed bandpass filters using LPFGs, and some of them have studied the topics based on a core mode blocker as shown in Fig. 1. In Fig. 1, the LPFG₁ is used to interact between core and cladding at resonant wavelength, and light existing in the core is extinguished by the core mode blocker. The light in the resonant wavelength is propagated through the cladding to the second LPFG. The resonant light existing in the cladding by the LPFG₂ is transferred back into the core.The central points of the research are to study the physical phenomenon [3, 4] and the manufacture of the bandpass filter [5-7, 9]. However the design of the flat-top bandpass filter [11] with specific customized wavelength band using an accurate analysis model was not proposed yet.

In the paper, we present the matrix model to analyze the

matrix model to analyze the LPFG structures with the core mode blocker. The proposed matrix model is a useful mathematical tool to describe the properties of the structure. We analyze the physical properties of the LPFG structure with a core mode blocker by using the proposed model. By using specially coupled feature of only the same modes in overlapped wavelength region, we demonstrate the design of the flat-top bandpass filter with the customized bandwidth.

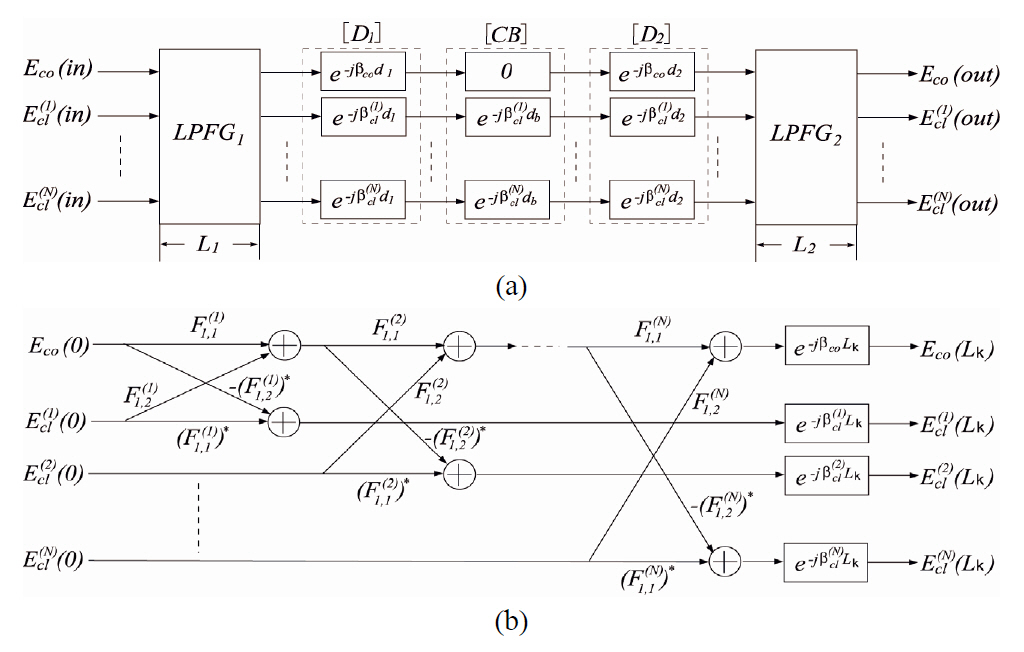
The structure in Fig. 1 is modeled as the FIR (Finite Impulse Response) filter block diagram as shown in Fig.2(a). Figure 2(b) is the signal flow graph to analyze both LPFG₁and LPFG₂, which is called the multiport lattice filter model [10-12]. Here, D₁ and D₂ are the delay of the diagonal matrix, CB is matrix for core mode blocker, E_co and E_cl⁽ⁱ⁾ are the E-fields (electric fields) of the fundamental core mode and the ith cladding mode, respectively. And β_co and β^cl_(i) are the propagation constant of the fundamental core mode and the ith cladding mode for the LPFGs, L₁ and L₂ are the length of LPFG₁ and LPFG₂, and d₁, d₂, and d_b are the length for D₁, D₂, and CB.

In Fig. 2(a), the E-fields coming into and out from the structure can be written to be

where

are diagonal matrices and

is a diagonal matrix with zero determinant.

By assuming the LPFG_k, (k = 1, 2) are uniform long period fiber gratings, we can easily get the matrix form of the (N+1)×(N+1) complex matrix M_k, (k = 1, 2) for the LPFG_k with codirectional interactions since the LPFG_k has the multiport lattice filter structure in [10] as follows:

where G^(p) is (N+1)×(N+1) identity matrix except for the four entries adopted from F^(p) in Fig. 2(b). The relation between G^(p) and F^(p) are as follows:

(Here, B_k,l denotes the (k, l) element of the matrix B.) The matrix DG represents the phase shift of the LPFG,

and

and

, L_k is the length of the LPFG_k, δ_p is the detuning factor for the pth cladding mode, and κ _p is the coupling coefficient between the fundamental core mode and the pth cladding mode [10-13].

Note that M_k in (2) can be regarded as a multiport lattice section. Because of the decoupling property of modes, the matrices G^(p) in M_k commute with each other so that the

2×2 subsections may be interchanged freely. If LPFG₁ and LPFG₂ are extended as piecewise uniform LPFGs, we can also easily get the Mk using the multiport lattice filter model [10]. Now, the overall transmission coefficient t ≡ E_co(out)？E_co(in) with E_cl⁽ⁱ⁾(in) = 0, (1≤i≤N) is easily seen to be t = Q_1,l, which is the (1,1)-element of Q.

As shown in Fig. 2(a), after the coupled light on the LPFG₁ is absorbed at CB, and then in the LPFG₂, the propagated light in the cladding is coupled with the same modes from cladding to core, due to the orthogonality of modes as shown in Fig. 2(b) [10]. Because the overall transmission is calculated as the complex multiplying of two bandpass filters, we cannot get the spectrum in the core if two filters have entirely different bandpass regions.

We analytically calculated the transmission spectrum curves for the concatenated LPFGs with a core mode blocker in the following examples by computing the transmission coefficient t = Q_1,l in (1). The parameters of the fiber used in these examples are as follows:

n_co = 1.449, n_cl = 1.444, n_ai = 1, r_co = 4.5㎛, r_cl = 62.5㎛ where n_cl is the refractive index of the cladding, n_air is the refractive index of air, r_co is the radius of the core, and r_cl is the radius of the cladding.

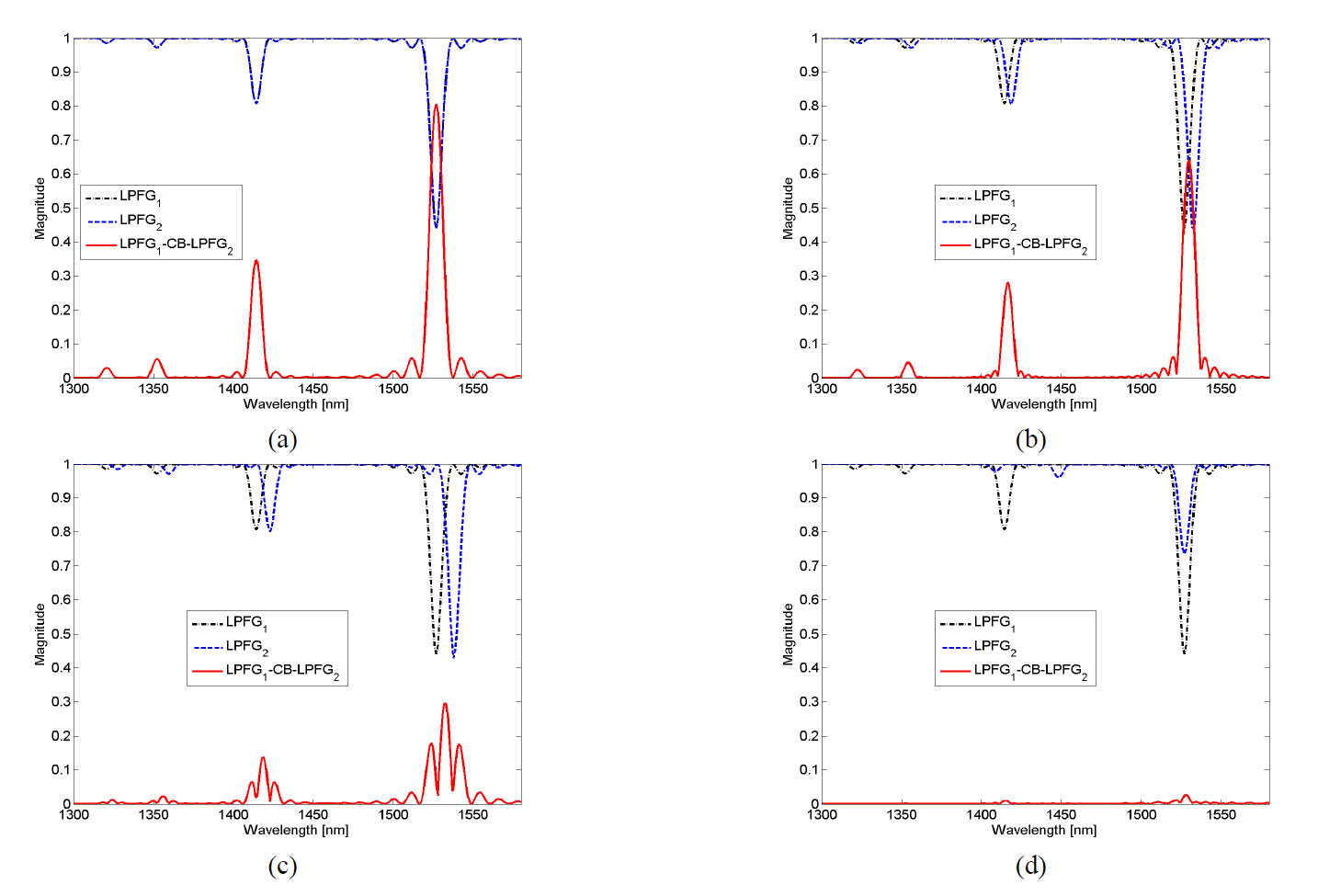
Figure 3 shows the transmission for the modes LP_0i, (i= 1,？,4) in the wavelength range between 1300 nm and 1580 nm, where LPFG₁ and LPFG₂ have uniform gratings.Their lengths are L₁ = 100Λ₁ and L₂ = 100Λ₂, respectively,the grating period for LPFG₁ is Λ₁ = 441.24 ㎛, Λ₂ for LPFG₂ is varied (441.24 ㎛ for Fig. 3(a), 443.44 ㎛ for Fig. 3(b), 445.65 ㎛ for Fig. 3(c), and 501.28 ㎛ for Fig.3(d)) and their induced index changes are Δn₁ = n₂ = 0.00011,respectively. The length of the D₁ and the D₂ are d₁ = 400 Λ₁ and d₂ = 400Λ₁, respectively. The length of the CB is assumed to be d_b = 0.

To analyze the properties of the concatenated LPFGs with the core mode blocker, we have calculated the transmission spectra along the change of the Λ₂ as shown in Fig 3. Figures 3(a)-3(c) show the transmission along the overlapped region of the spectrum band of the same modes. We can only get the bandpass spectra by coupling the same modes in the overlapped region. Figure 3(d) shows the transmission for the coupling with the different modes (LP₀₄ of LPFG₁ and LP₀₃ for LPFG₂). From the result, we know that the bandpass filter cannot be obtained from coupling the different modes.

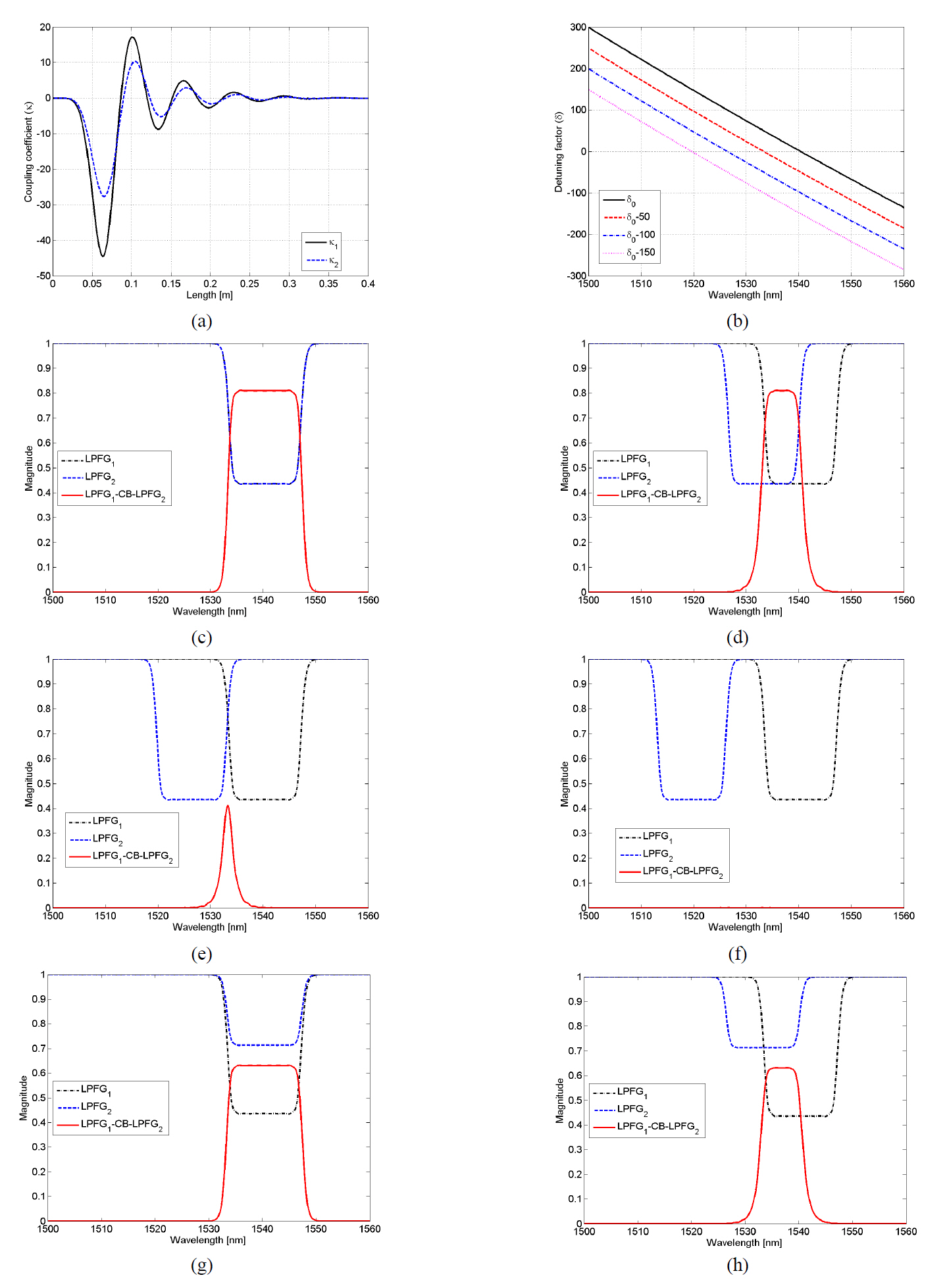
We can design a flat-top bandpass filter with the customized bandwidth using the property of coupling with the same modes and the overlapped band. We have synthesized

the tunable flat-top filter by considering a single cladding mode as shown in Fig. 4. We have utilized the coupling coefficients κ and the detuning factors δ, respectively, as shown in the Figs. 4(a) and 4(b). The coupling coefficients in Fig. 4(a) can be found by the Gel’fand-Levitan-Marchenko coupled equations [14, 15].

The κ₁ in Fig. 4(a) is used for the LPFG₁ and LPFG₂ of Figs. 4(c)-4(f). In Fig. 4(b), the δ₀ is used for the LPFG₁ and LPFG₂ is used the δ₀ for Fig. 4(c), the δ₀-50 for Fig. 4(d), the δ0-100 for Fig. 4(e), and the δ0-150 for Fig. 4(f). We have assumed the delay is d₁ = d₂ = 0 and the core mode blocker is CB = diag(0,1,1？,1), ideally. The 3dB bandwidth of the LPFG₁ and LPFG₂ is 13.9nm. In the case, we can control the bandwidth of the flat-top bandpass filter in the wavelength range less than 13.9nm± ε (where ε is a small variation by calculating the equation (1).). The 3dB bandwidth of the obtained flat-top filter in Figs. 4(c) and 4(d) are 14.2nm (ε = 0.3 nm) and 8nm, respectively.

From the results, we can observe that the bandwidth of the bandpass is changed along the overlapped band region of the flat-top band-rejection of both LPFG₁ and LPFG₂. If we can make the ideal band-rejection filter, we can synthesize a sharp bandpass filter with the customized bandwidth as well as the bandpass filters with a tunable bandwidth. Especially,if the bandwidth of LPFG₁ and LPFG₂ aren’t overlapped as shown in Fig. 4(f), we cannot synthesize the desired filter.

We also demonstrated the transmission along the overlapped region, when the coupling coefficients are different as shown in Figs. 4(g) and 4(h). The coupling coefficients κ₁ for the LPFG₁ and κ₂ the LPFG₂ are utilized as shown in Fig.4(a). The detuning factors δ for Figs. 4(g) and 4(h) are the same ones as for Figs. 4(c) and 4(d). We have also used the delay and the core mode blocker as above examples.

From the Fig. 4(g) and 4(h), we have obtained similar results to Figs. 4(c) and 4(d) although the LPFG₁ and LPFG₂ have different magnitude levels. The 3 dB bandwidth of the LPFG₂ is 14.1 nm. The 3 dB bandwidth of the obtained flat-top filter in Figs. 4(c) and 4(d) are 14.2 nm(ε = 0.1 nm) and 8 nm, respectively. The results show that the magnitude level of the flat-top bandpass filter is dependent on the magnitudes of the LPFG₁ and LPFG₂.

The analytical model for the LPFG with the core mode blocker is proposed. We have also analyzed and described the physical phenomenon of the structure by using the proposed model. We have proposed a design method of the flat-top bandpass filter with customized bandwidth. We have also demonstrated, through computer simulations, the bandwidth of the flat-top filters controlled by tuning the overlapped band region.